[Game Mathematics] 삼각 함수(Trigonometric Functions)
👻 삼각 함수
이번 시간에는 게임의 수학 법칙 중 필요한 개념중 하나인 삼각 함수에 대해 알아보자. 수학에서 삼각 함수(Trigonometric Functions)는 각의 크기를 삼각비로 나타내는 함수이다. 3개의 기본적인 함수가 있으며 각각 사인(sine), 코사인(cosine), 탄젠트(tangent)라고 한다. 게임 자체에서 필요한 삼각 함수의 개념을 알게되면 행렬을 이용하여 물체 회전이 일어날 때의 각도를 삼각 함수로 나타낼 수 있다.
🌱 피타고라스 정리
기하학에서 피타고라스 정리는 직각 삼각형에서 빗변 길이의 제곱은 다른 두 변의 길이의 제곱의 합과 같다는 법칙이다.
빗변이 a, 두 직각변이 각각 b, c 일 때
a² = b² + c²이 성립한다.
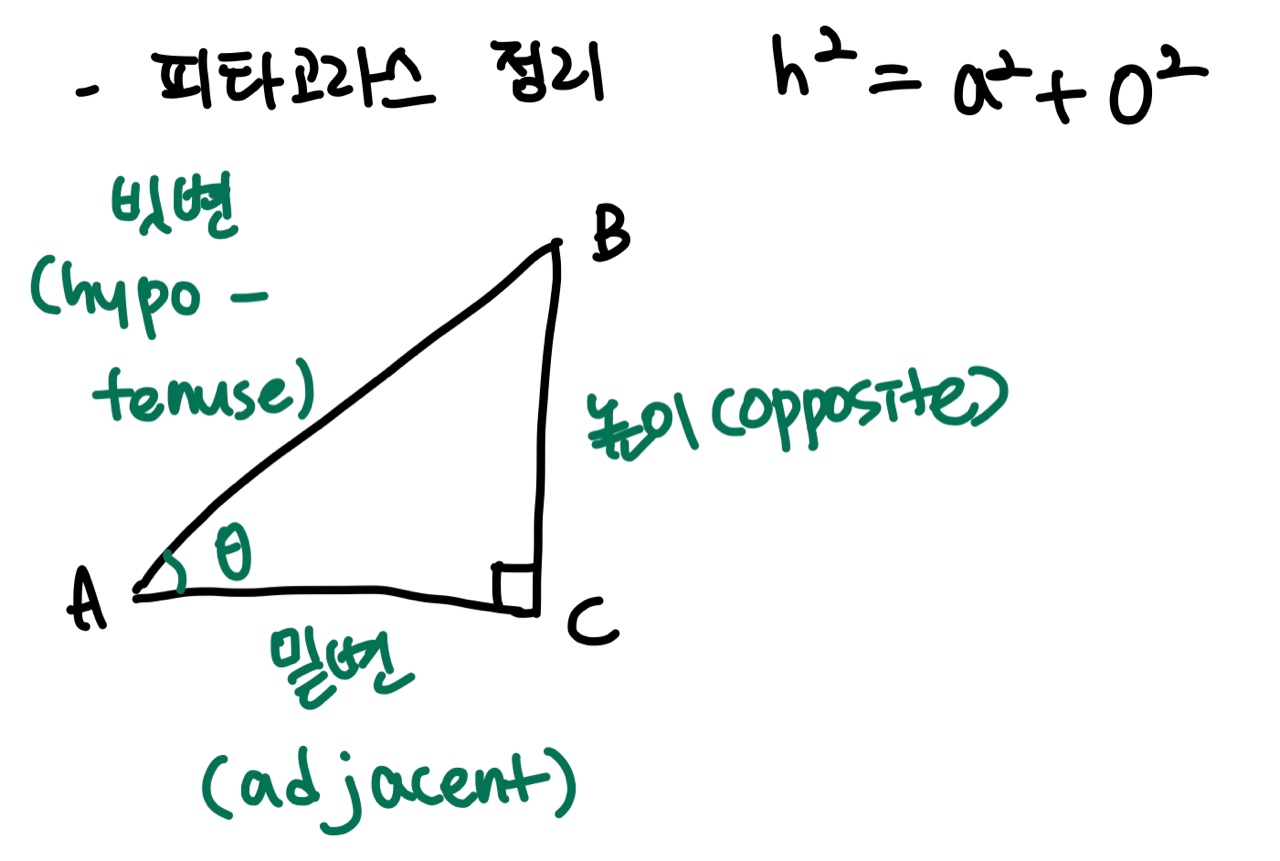
위에서 삼각 함수는 각의 크기를 삼각비로 나타내는 함수라고 했었다. 사인, 코사인, 탄젠트 함수는 직각 삼각형에서 다음과 같이 정의할 수 있다.
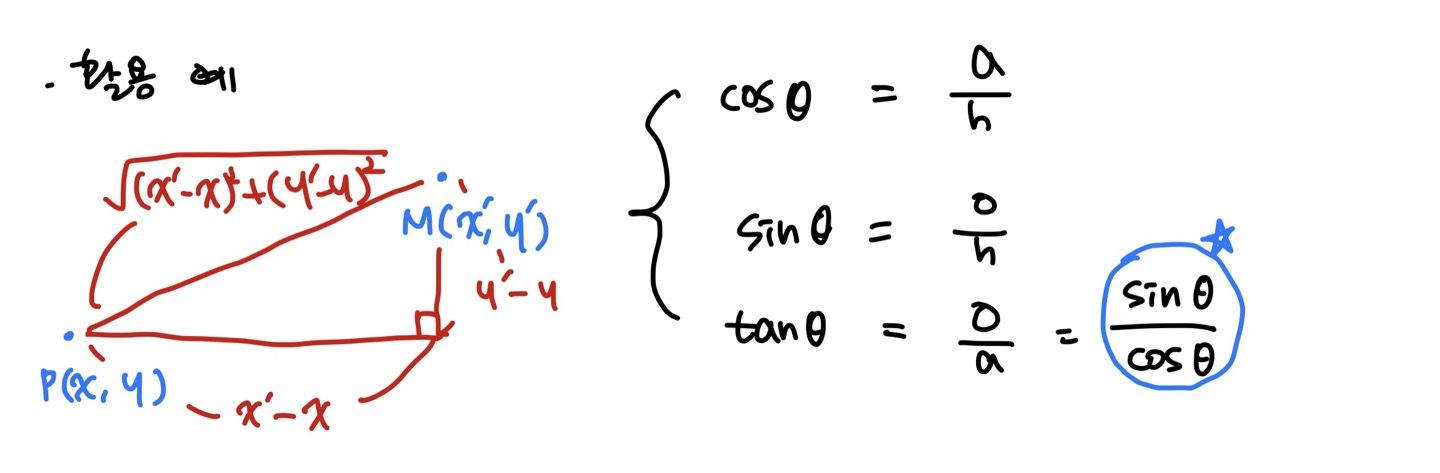
🌱 단위원
단위원(Unit Circle)은 좌표평면에서 원점을 중심으로 하고 반지름 r의 길이가 1인 원을 의미한다.위의 삼각 함수를 단위원을 통해 정의할 수도 있다.
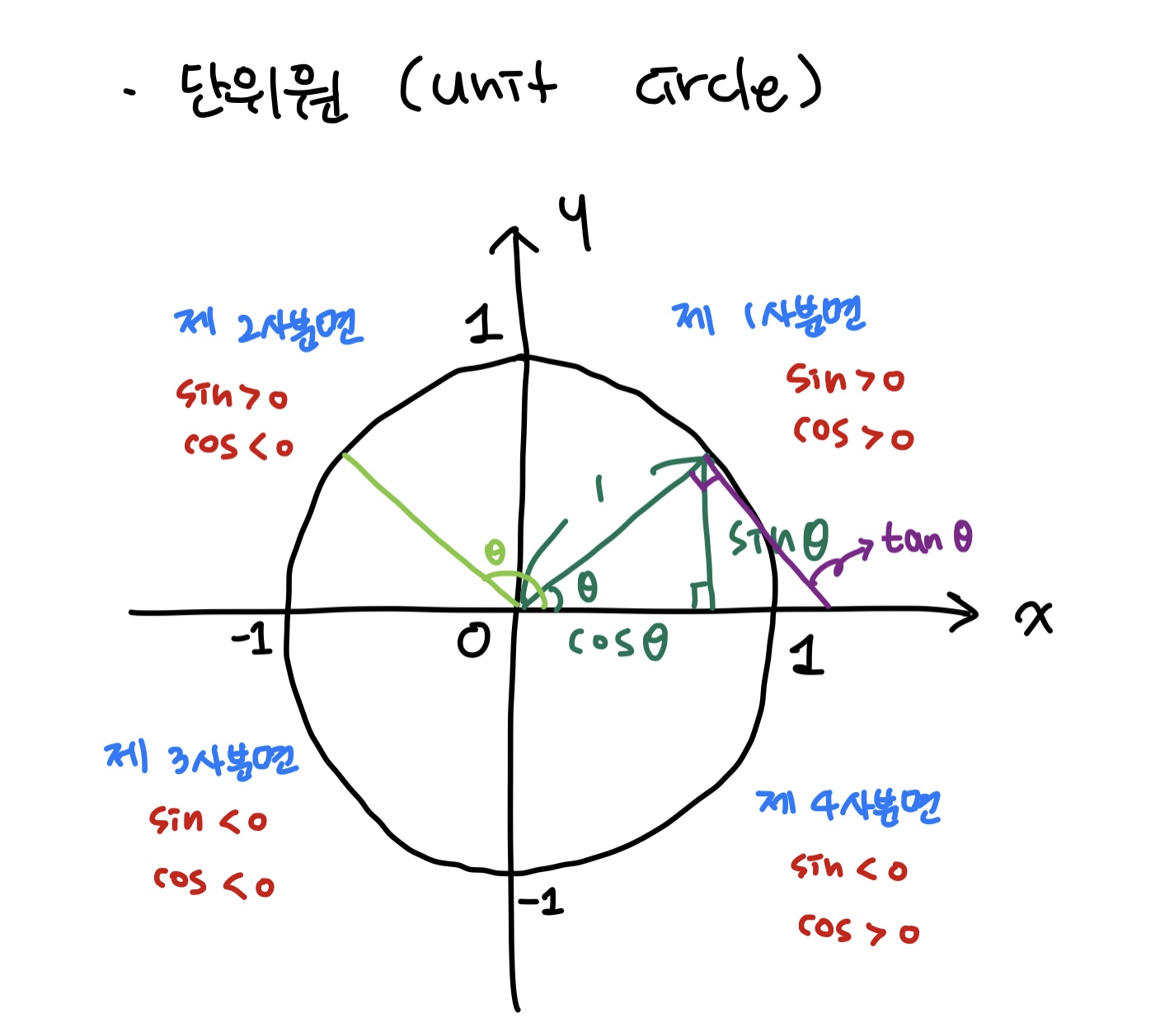
🌱 라디안
위의 단위원에서 호의 길이가 1일 때 각도의 단위를 라디안(Radian)이라 정의한다.

🌱 삼각 함수의 그래프
사인, 코사인, 탄젠트의 그래프는 다음과 같다.
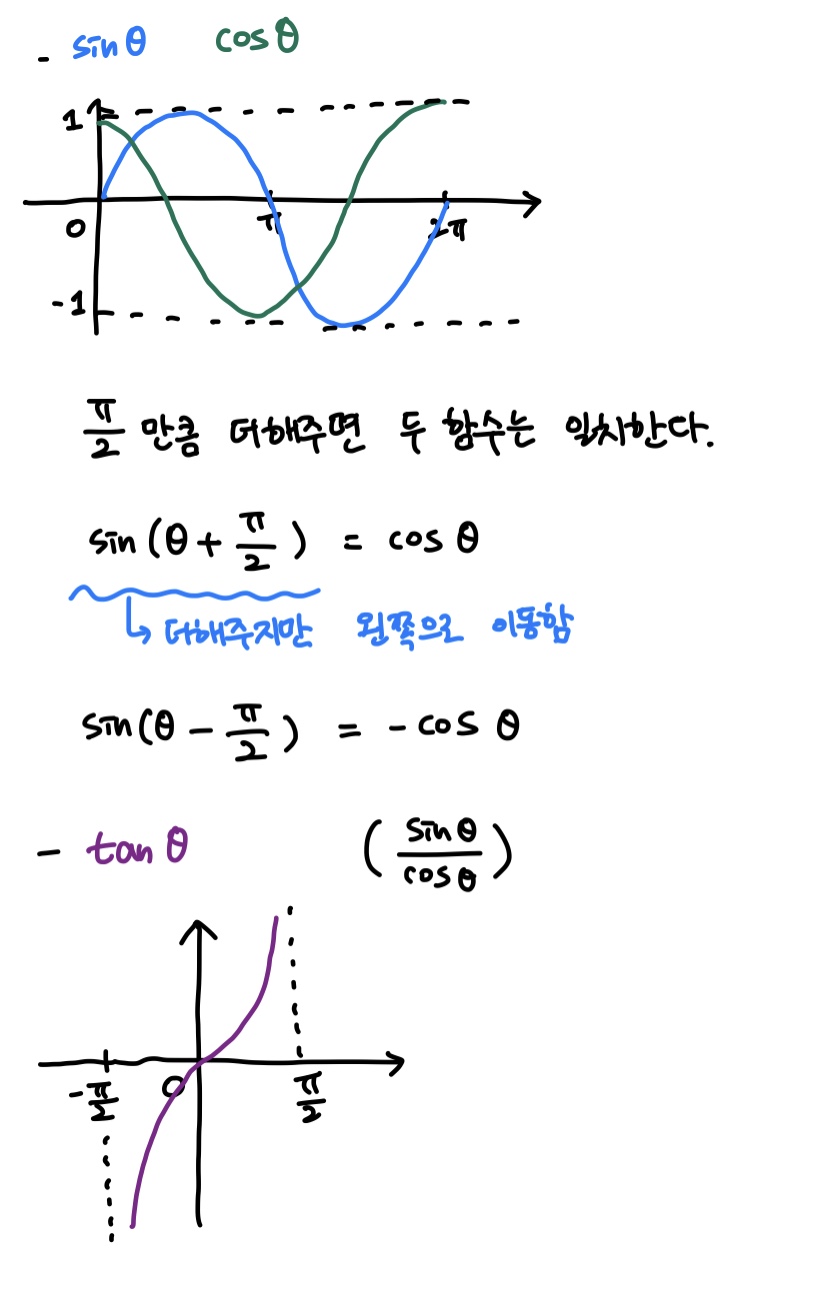
각 식을 통해 다음과 같은 결과를 도출할 수 있다.
- sinθ, cosθ
-∞ ≤ θ ≤ ∞,-1 ≤ sinθ, cosθ ≤ 1
- tanθ
-θ - π/₂ < θ < θ + π/₂,-∞ ≤ tanθ ≤ ∞
일반적으로
θ는 무제한이며 일정한 증감 규칙을 가진다. 사인과 코사인은 무제한 범위가 그대로지만 탄젠트의 경우π/₂씩 일정한 간격을 가진다.
🌱 역함수
임의의 각도에 대한 삼각비를 나타내는 일반 삼각 함수의 역으로, 임의의 삼각비에 대한 각도를 도출해내는 함수이다. arc를 붙여 나타낸다.
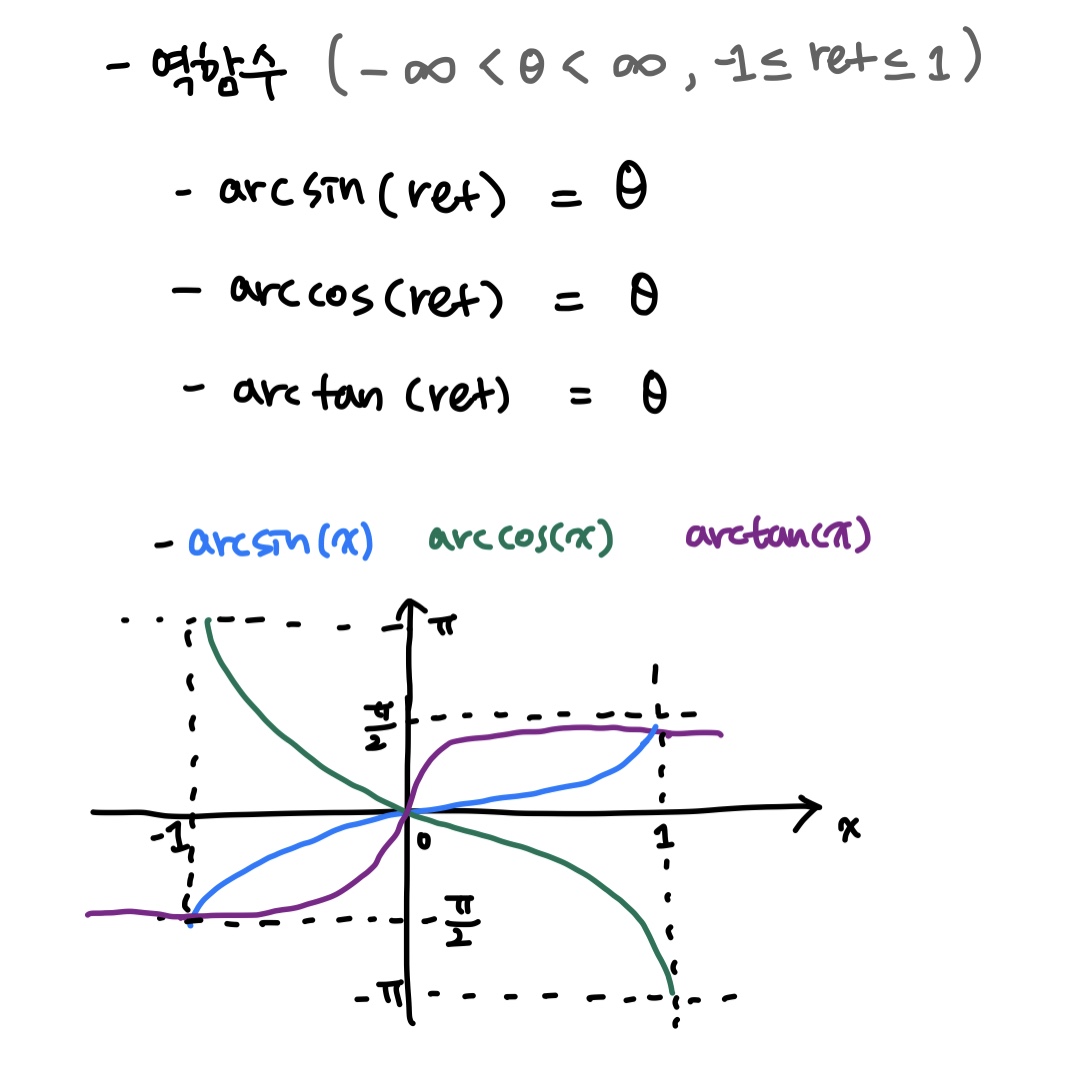
역함수는 일반 삼각함수의 그래프가 약간 변형된 모양(돌리고 뒤집고..)이지만 도출되는 결과는 모두 같다.
👻 자주 사용하는 공식
삼각 함수를 이용한 공식 중에 자주 사용하는 공식 두 가지를 알아보자.
🌱 cos 법칙
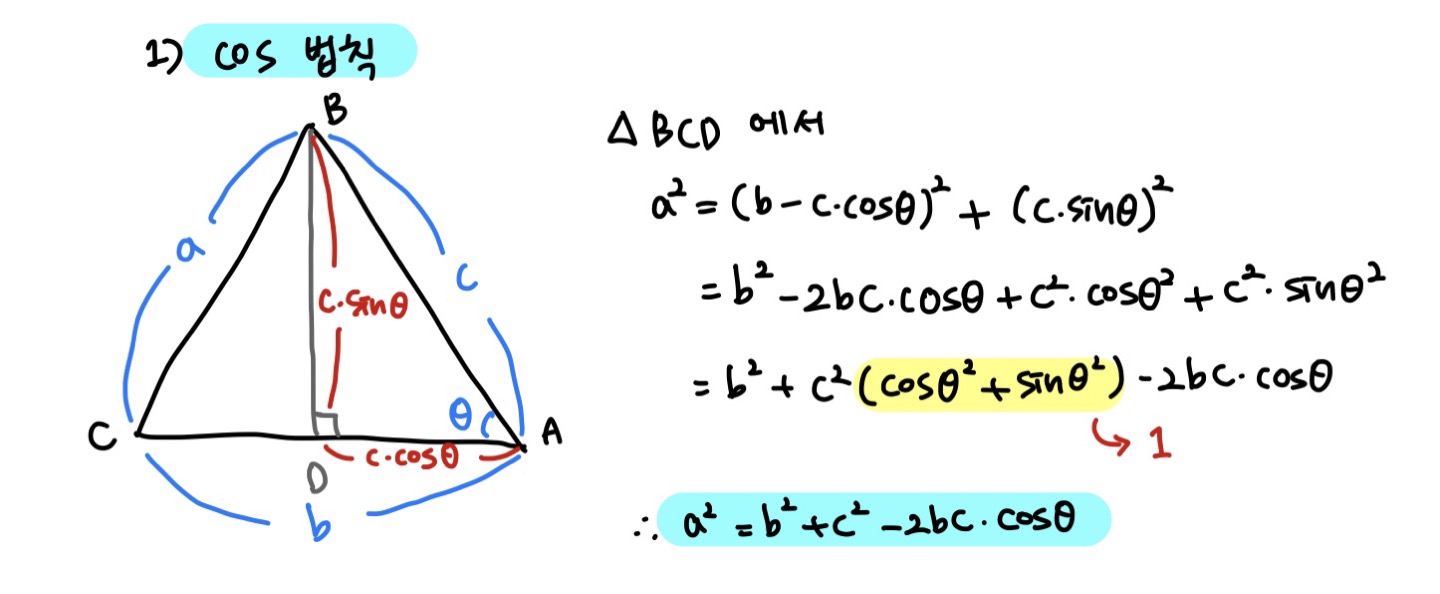
코사인 법칙은 삼각형의 세 변과 한 각의 코사인 사이에 성립하는 정리로 삼각형의 변의 길이와 각의 크기를 찾을 때 유용하다. 피타고라스 정리로 증명할 수 있다.
🌱 cos 덧셈 정리
삼각 함수 덧셈 정리 중 코사인 덧셈 정리는 자주 사용된다. 식은 아래와 같다.
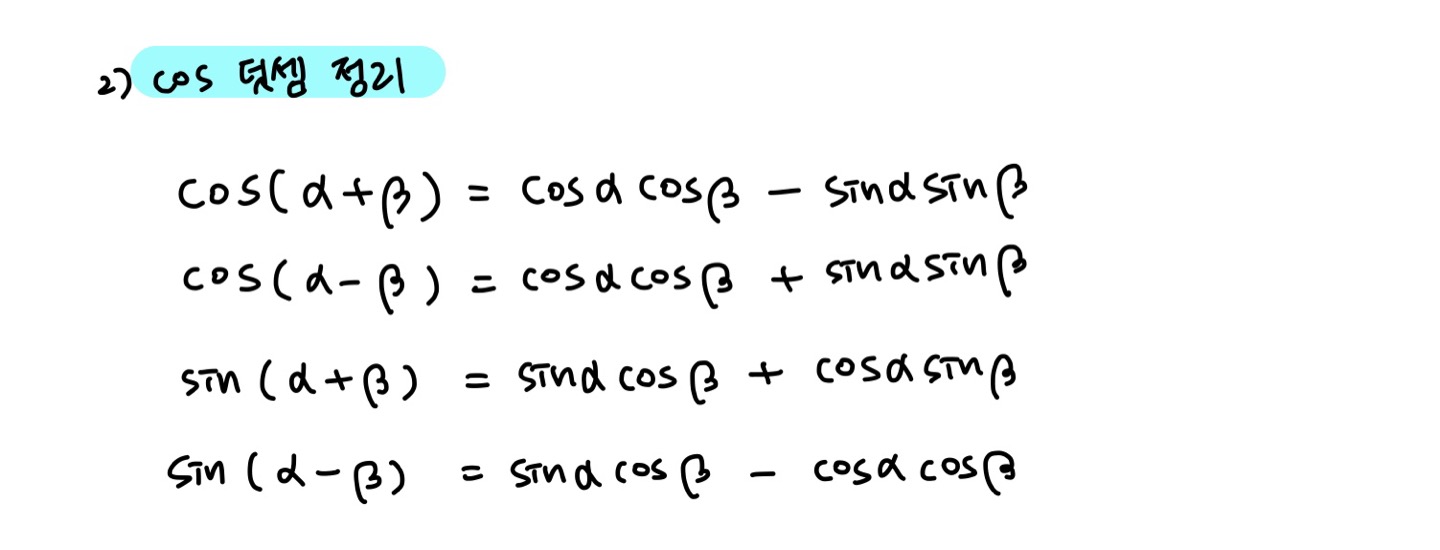
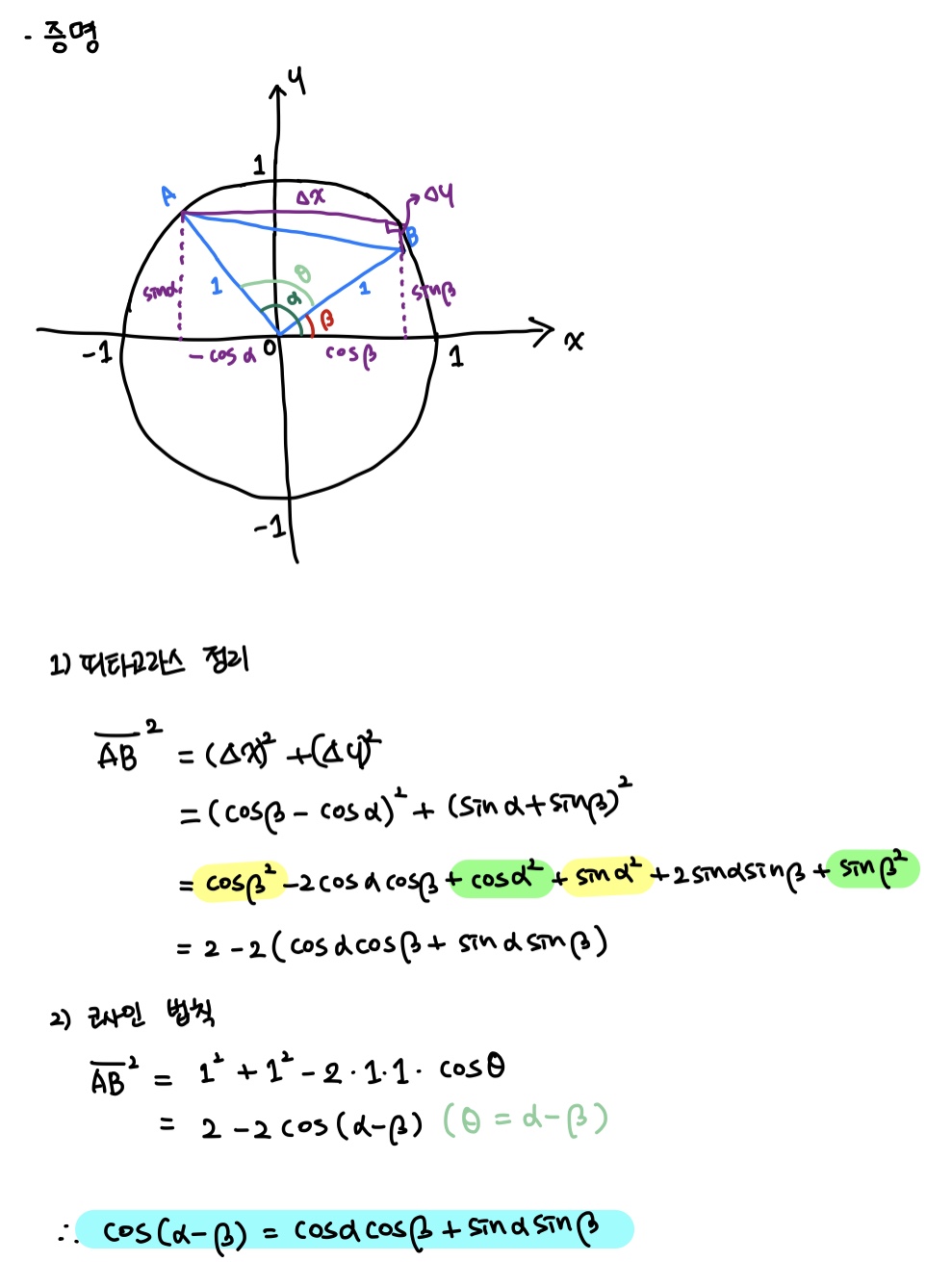
단위원, 피타고라스 정리, 코사인 법칙을 이용해 증명할 수 있다.
👻 글을 마치며
이번 시간에는 삼각 함수에 대해 알아보았다. 오랜만에 고등 수학을 접해서 재밌기도하고 정신없기도 했다. 그래도 알고 있던 것들이라 복습하는 느낌이 더 컸다. 게임 수학을 처음에 들었을 땐 많이 어려울까봐 걱정했었는데 그래도 다 아는 것들이라 약간 걱정을 덜 수 있었던 것 같다. 이제 코드에 접목하는 게 문제..
Leave a comment