[Computer Graphics] #5-1. 정점 처리 연습문제 풀이

👻 연습문제 풀이

5장 정점 처리 챕터의 연습문제는 총 14개이다.

---

🌱 1

• 문제

두 개의 2차원 비표준 직교정규 기저 {a, b}와 {c, d}가 주어졌을 때, {a, b}에서 정의된 벡터를 {c, d}에서 정의된 벡터로 변환하는 2 × 2 행렬을 계산하라.

• 풀이

---

🌱 2

• 문제

두 개의 3차원 비표준 직교정규 기저 {a, b, c}와 {d, e, f}가 주어졌을 때, {a, b, c}에서 정의된 벡터를 {d, e, f}에서 정의된 벡터로 변환하는 3 × 3 행렬을 계산하라.

• 풀이

---

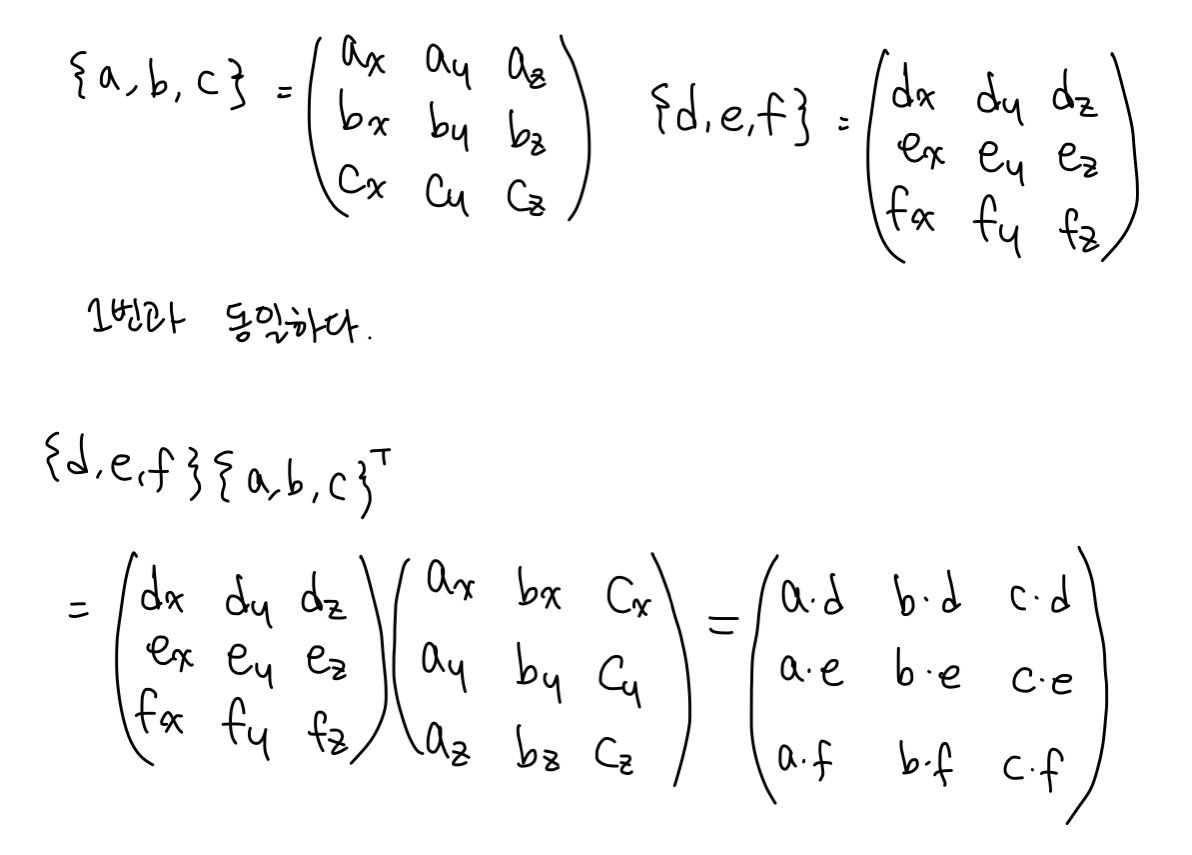
🌱 3

• 문제

두 개의 직교정규 벡터 a, b를 기준으로 하는 축소확대를 생각해 보자. a, b 방향으로의 축소확대 인자는 각각 s_a, s_b로 표기한다. 한편, a, b 중 어느 것도 표준 기저 벡터(e₁, e₂)와 일치하지 않는다. 우리가 구하고자 하는 축소확대 행렬은 세 개의 2 × 2 행렬의 곱으로 표현된다. 각각의 행렬을 계산하라.

• 풀이

---

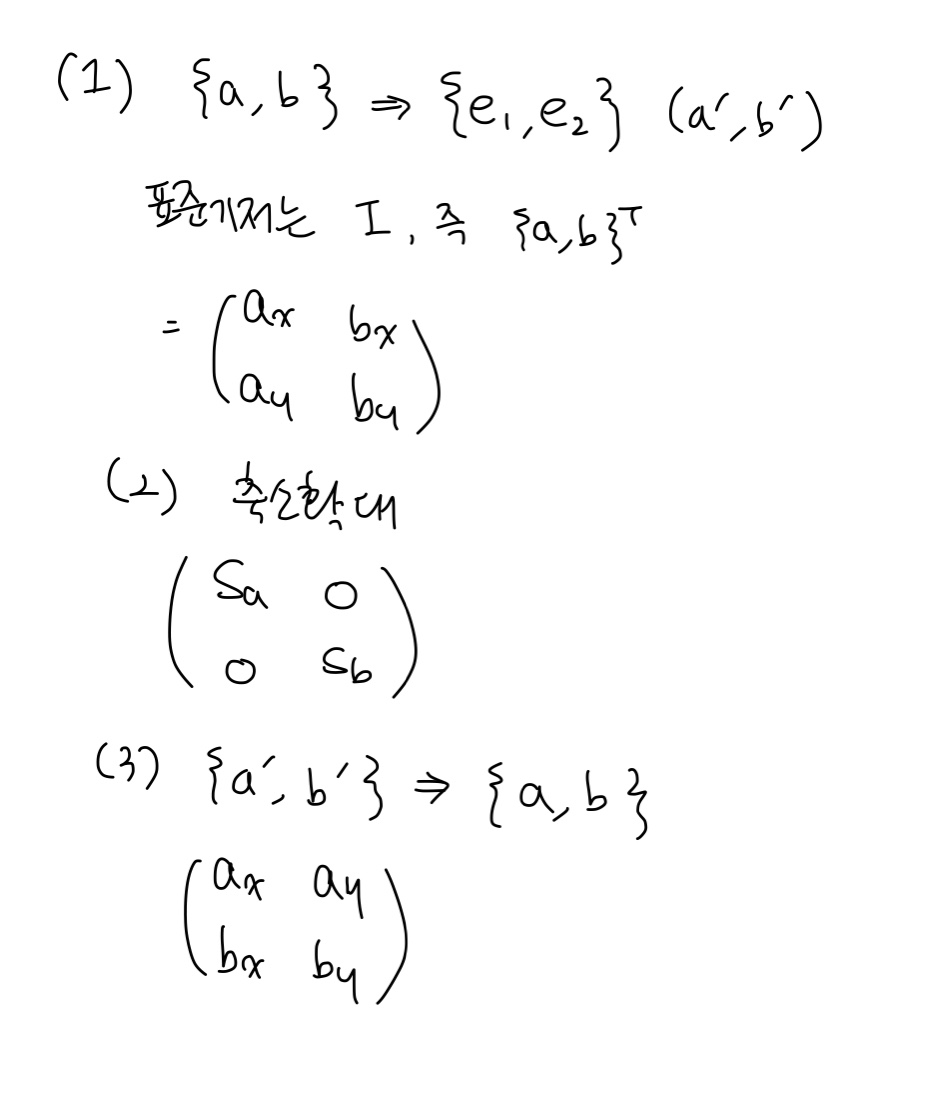
🌱 4

• 문제

세 개의 직교정규 벡터 a, b, c를 기준으로 하는 축소확대를 생각해 보자. a, b, c 방향으로의 축소확대 인자는 각각 s_a, s_b, s_c로 표기한다. 한편, a, b 중 어느 것도 표준 기저 벡터(e₁, e₂, e₃)와 일치하는 것은 없고, a, b, c 간에는 a × b = c의 관계가 성립한다. 우리가 구하고자 하는 축소확대 행렬은 세 개의 3 × 3 행렬의 곱으로 표현된다. 각각의 행렬을 계산하라.

• 풀이

---

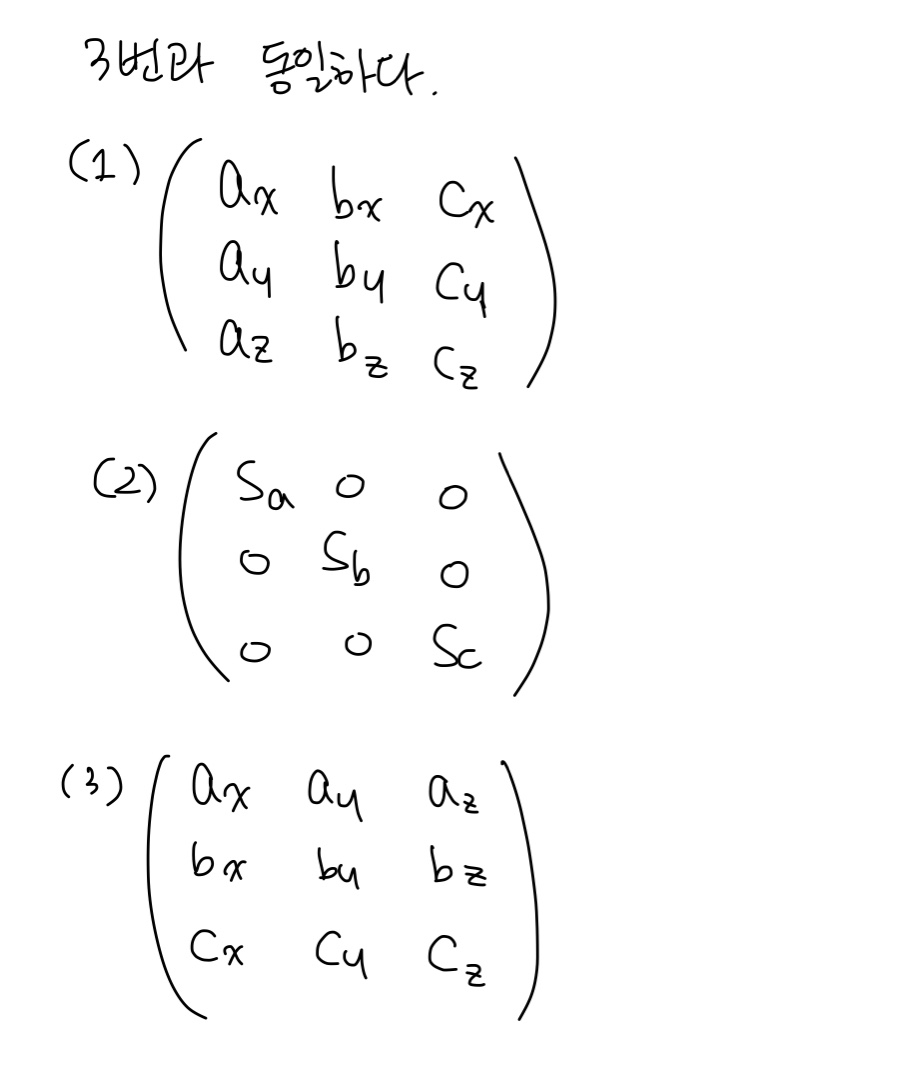
🌱 5

• 문제

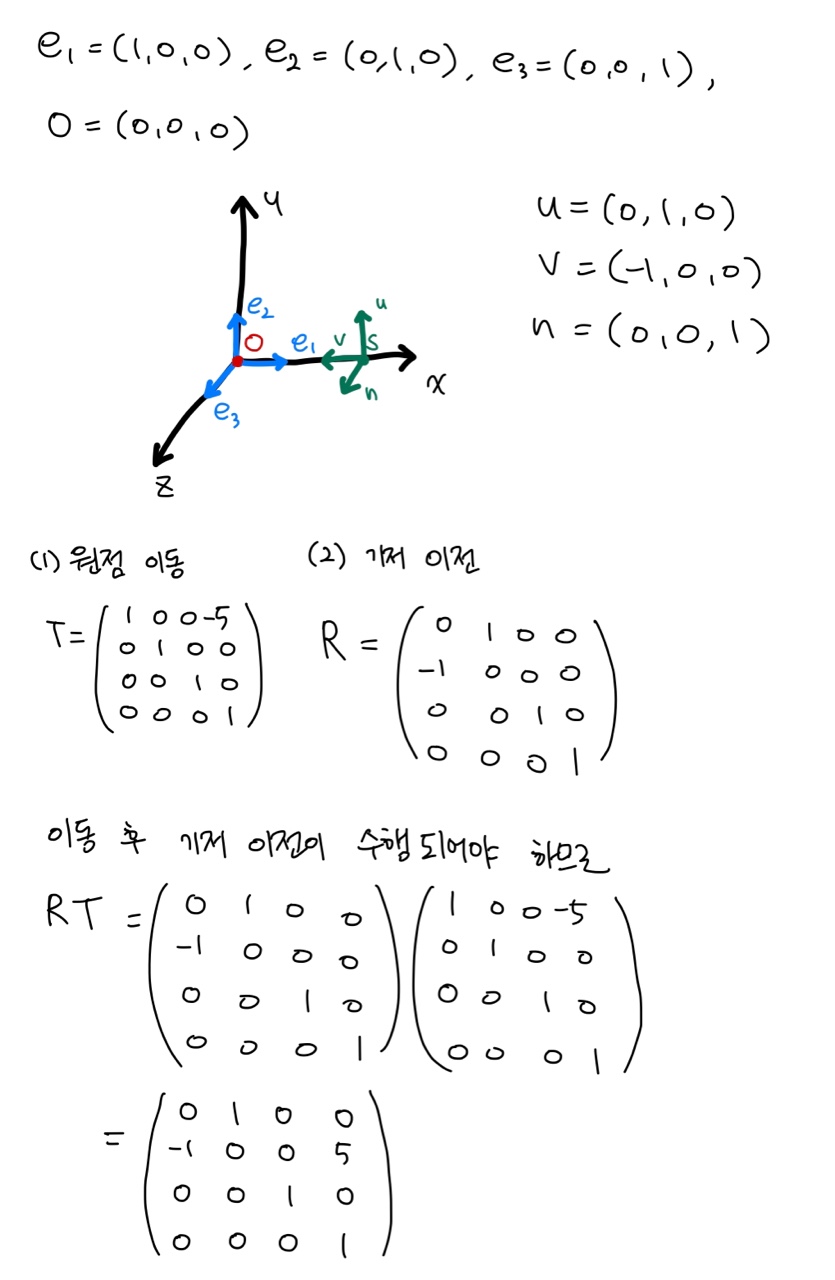
월드 공간의 기저 벡터와 원점은 다음과 같다: e₁ = (1, 0, 0), e₂ = (0, 1, 0), e₃ = (0, 0, 1), O = (0, 0, 0). 한편, 월드 공간의 (5, 0, 0)에 원점이 있고 기저가 {(0, 1, 0), (-1, 0, 0), (0, 0, 1)}인 좌표계를 S라고 표기하자. 월드 공간의 점을 S로 변환하는 행렬을 정의하라.

• 풀이

---

🌱 6

• 문제

카메라 파라미터가 다음과 같이 주어졌다: EYE = (0, 0, -√3), AT = (0, 0, 0), UP = (0, 1, 0).

(a) 카메라 공간의 기저와 원점은 무엇인가?
(b) 뷰 변환은 이동에 이은 회전으로 정의된다. 두 행렬을 계산하라.

• 풀이

---

🌱 7

• 문제

카메라 파라미터가 다음과 같이 주어졌다: EYE = (0, 0, 3), AT = (0, 0, -1), UP = (-1, 0, 0).

(a) 카메라 공간의 기저와 원점은 무엇인가?
(b) 뷰 변환은 이동에 이은 회전으로 정의된다. 두 행렬을 계산하라.

• 풀이

---

🌱 8

• 문제

카메라 파라미터가 다음과 같이 주어졌다: EYE = (0, 0, 3), AT = (0, 0, -1), UP = (-1, 0, 0). 카메라 공간의 점을 월드 공간으로 변환하는 행렬을 계산하라. 이는 뷰 변환 행렬이 아니라 그 역행렬임에 유의하라.

• 풀이

---

🌱 9

• 문제

월드 공간에서 두 개의 카메라 파라미터 군 {EYE, AT, UP1}과 {EYE, AT, UP2}가 주어졌다. 각 좌표는 다음과 같다: EYE = (18, 8, 0), AT = (10, 2, 0), UP1 = (0, 8, 0), UP2 = (-13, 2, 0). 이를 기반으로 정의된 두 개의 카메라 공간이 일치하는지 아닌지 기술하라.

• 풀이

---

🌱 10

• 문제

두 개의 카메라 공간 S₁과 S₂가 주어졌을 때, S₁의 점을 S₂로 변환하는 한 가지 방법은, S₁의 점을 먼저 월드 공간으로 변환한 후 이 월드 공간 점을 S₂로 변환하는 것이다.

(a) S₁은 다음과 같은 카메라 파라미터에 의해 정의된다: EYE = (0, 0, 3), AT = (0, 0, -1), UP = (-1, 0, 0). S₁의 점을 월드 공간으로 변환하는 행렬을 계산하라.
(b) S₂는 다음과 같은 카메라 파라미터에 의해 정의된다: EYE = (0, 0, -3), AT = (0, 0, 0), UP = (0, 1, 0). 월드 공간 점을 S₂로 변환하는 행렬을 계산하라.

• 풀이

---

🌱 11

• 문제

월드 공간이 왼손 좌표계를 가진다고 가정하자. 이 월드 공간에서 카메라 파라미터가 다음과 같이 주어졌다: EYE = (0, 0, 3), AT = (0, 0, -1), UP = (-1, 0, 0).

(a) 카메라 공간 역시 왼손 좌표계로 정의된다고 가정하자. 이 카메라 공간의 기저를 계산하라.
(b) 뷰 변환을 계산하라.

• 풀이

---

🌱 12

• 문제

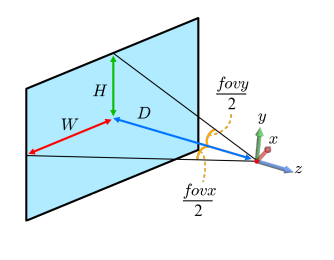
아래 그림은 뷰 프러스텀을 z축에 수직으로 자른 단면이다. 통상적인 fovy, aspect, n, f 대신 fovx, fovy, n, f가 주어졌는데 여기서 fovx는 x축 기준의 시야각을 의미한다. 한편, D는 카메라로부터 단면 중심까지의 거리이다. aspect를 fovx와 fovy의 함수로 정의하라.

• 풀이

---

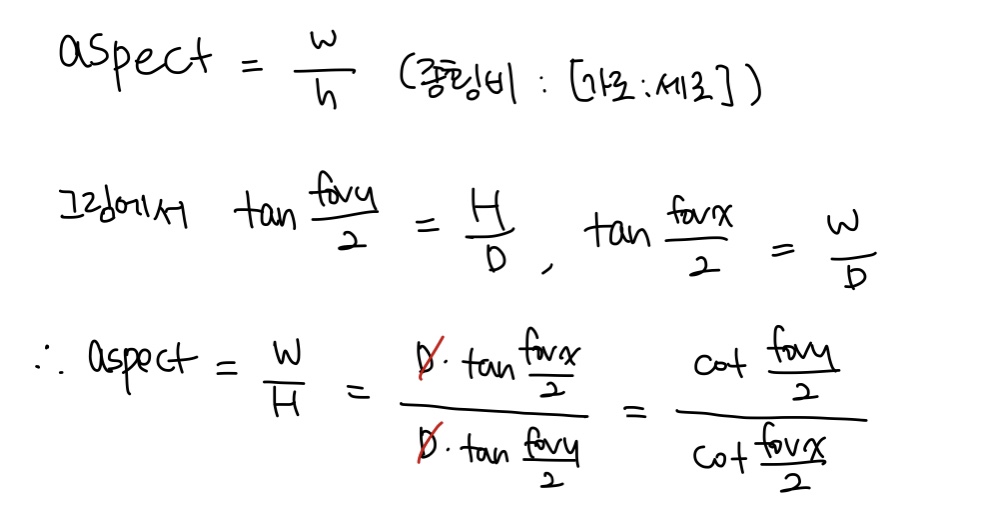
🌱 13

• 문제

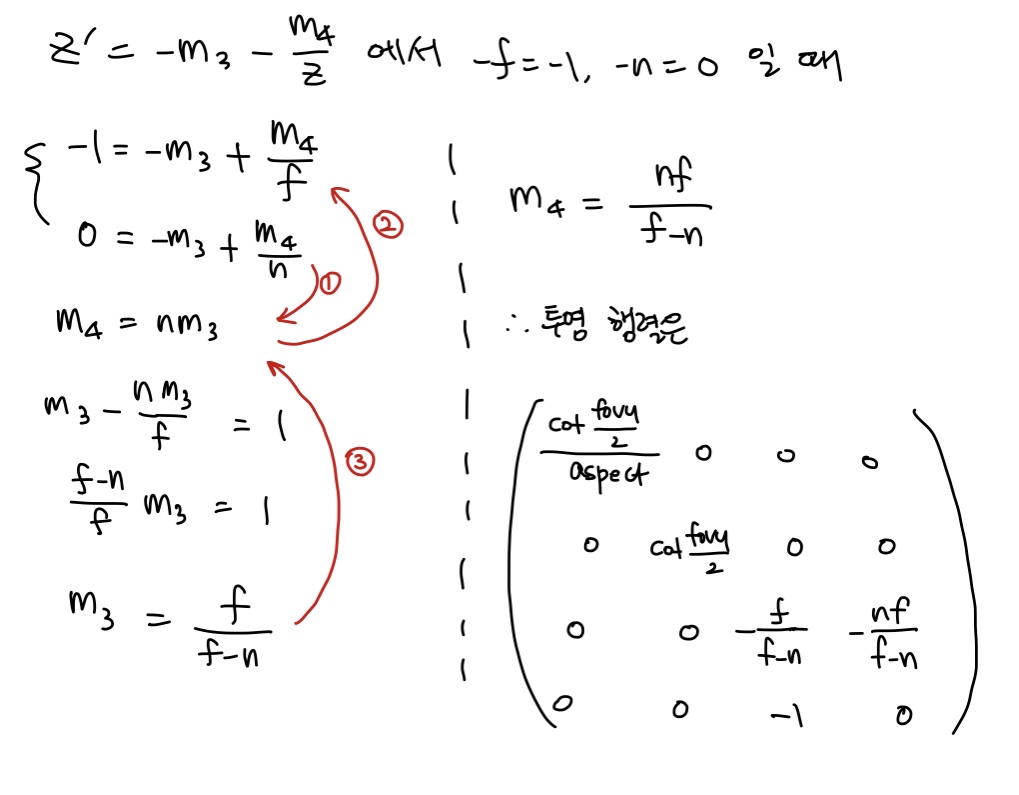
우리는 5.4.3절에서 투영 변환 이후의 z범위가 [-1, 1]인 것을 이용하여 투영 행렬을 계산하였다. 클립 공간 뷰 볼륨의 x와 y범위는 [-1, 1]이지만 z범위는 [-1, 0]이 되도록 바꿨다고 가정하자. 이 경우, 투영 행렬을 계산하라.

• 풀이

---

🌱 14

• 문제

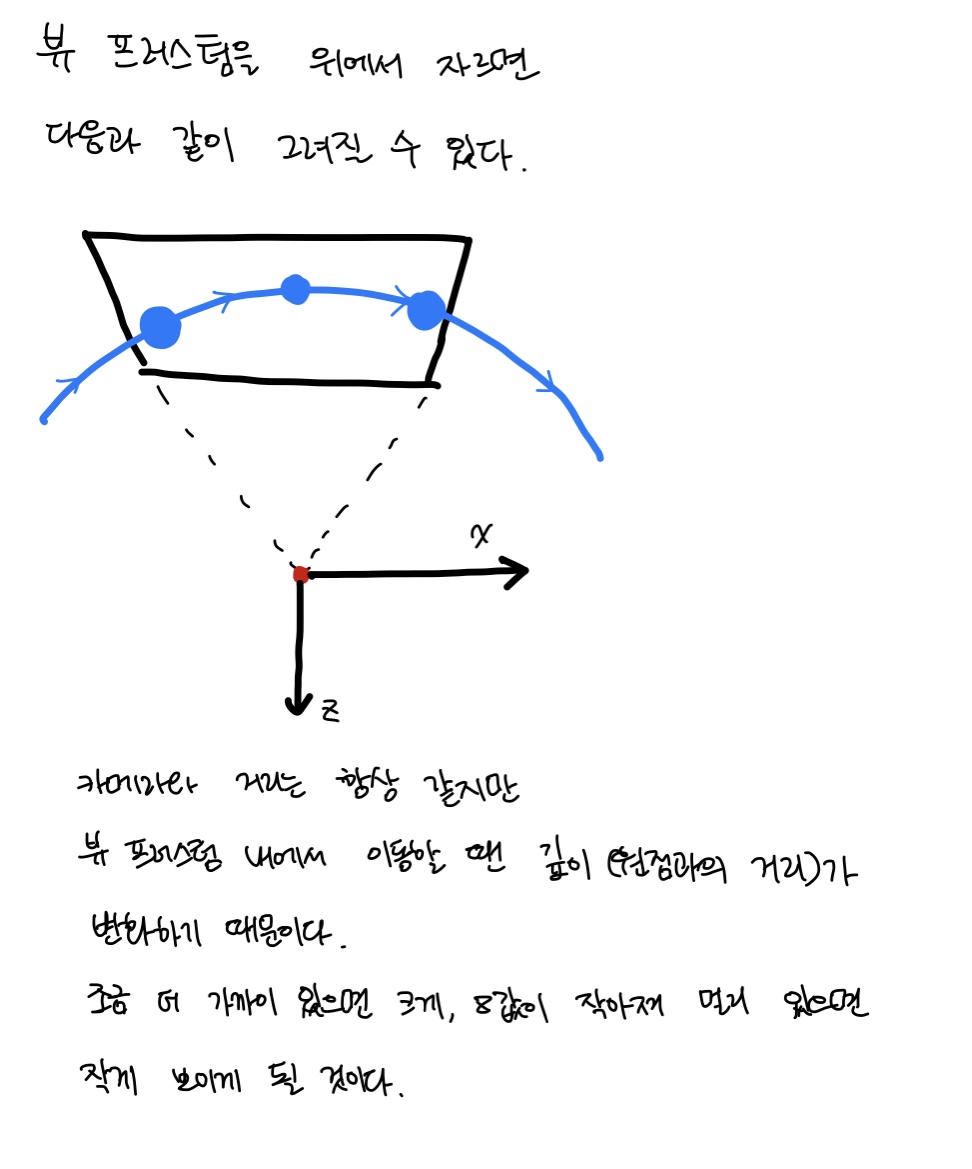
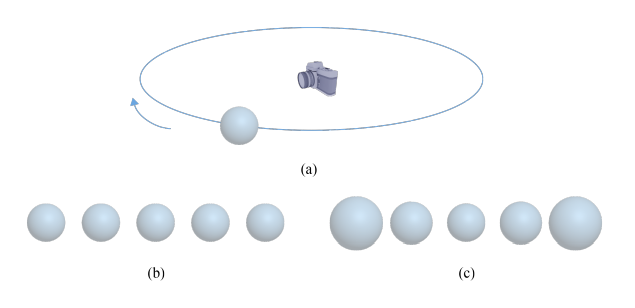
다음 그림 (a)에서 구는 고정된 카메라를 중심으로 원 운동을 한다. GPU 파이프라인을 이용해 이 구를 일정한 시간 간격으로 연속해서 렌더링하자. 카메라로부터 구 까지의 거리는 항상 일정하므로, 우리는 그림 (b)와 같은 결과를 예상할 수 있다. 하지만, 실제 렌더링 결과는 그림 (c)와 같다. 즉, 구가 뷰 프러스텀으로 막 진입했을 때 가장 크지만, 계속 작아지다가 카메라 공간의 -n축에 놓였을 때 최소 크기에 도달한다. 그 이후 다시 커지다가 뷰 프러스텀을 벗어날 때 최대 크기에 도달한다. 왜 이런 현상이 발생하는가?

• 풀이

---

👻 글을 마치며

이번 시간에는 정점 처리와 관련된 연습문제를 풀어보았다. 문제의 양이 많기도하고 워낙 행렬 계산식이 많아서 시간이 꽤나 걸렸던 것 같다. 하지만 응용문제를 풀고나니 개념에 한 걸음 더 가까이 다가가게 된 것 같고 모르는 문제들을 스터디원들과 함께 풀이하며 공부하니 두 배로 이해가 잘 되었던 것 같다.

---

출처
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처

관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음