[Computer Graphics] #5. 정점 처리
👻 정점 처리
GPU는 폴리곤 메시를 입력으로 받아 스크린에 그려질 2차원 형태로 바꾸고, 이 2차원 폴리곤 내부를 차지하는 픽셀(Pixel)들의 색상을 결정한다. 이 픽셀들은 컬러 버퍼(Color Buffer)에 기록되는데, 이는 스크린에 나타날 픽셀 전체를 저장하는 메모리 공간을 말한다. 컬러 버퍼는 주기적으로 스크린으로 복사된다.
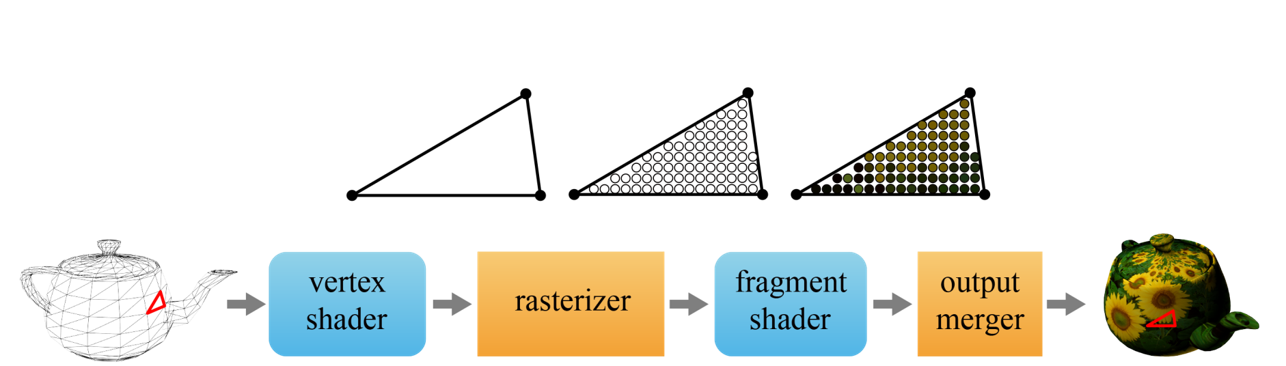
GPU 렌더링은 파이프라인(Pipeline) 구조로 구현된다. 파이프라인은 한 단계의 결과물이 다음 단계의 입력으로 사용되는 일련의 데이터 처리 단계를 의미한다. 드로우 콜(Draw Call)에 의해 GPU 안으로 입력값이 들어가게 되며 폴리곤 메시들의 정점은 정점 배열에 저장된다.
드로우 콜(Draw Call) : GPU에게 연산을 수행하라는 명령을 호출하는 것을 의미한다.
정점 쉐이더(Vertex Shader)가 이러한 정점을 하나씩 불러들이면서 변환을 비롯한 다양한 연산을 수행한다. 쉐이더(Shader)는 프로그램과 동의어이며 GPU 렌더링을 위해선 정점 쉐이더와 프래그먼트 쉐이더(Fragment Shader)라는 두 가지 프로그램을 작성해야 한다.
래스터라이저(Rasterizer) 단계에서는 인덱스 배열의 정보를 이용해 삼각형을 다시 하나씩 조립한다. 색상을 결정할 정보를 모아서 각 위치에 저장하는데, 여기서 삼각형 내부를 차지하는 프래그먼트(Fragment)를 생성하게 된다. 예비 픽셀, 후보 픽셀 정도로 이해하면 된다.
래스터라이저가 출력한 프래그먼트는 하나하나 프래그먼트 쉐이더로 입력되어, 라이팅과 텍스처링 등의 작업을 거쳐 색상이 결정된다.
출력 병합기(Output Merger)는 이러한 프래그먼트와 현재 컬러 버퍼에 저장된 픽셀 중 하나를 선택하거나 혹은 이들의 색을 결합하여 컬러 버퍼를 갱신한다.
위 이미지에서 표시된 파란색 단계는 GPU에서 프로그램과 같은 의미이며, 사용자가 직접 구현해줘야지만 실행되며 오렌지색 단계는 하드웨어로 고정되어있는 정해진 함수나 기능만 수행할 수 있는 단계(Legacy)이다.

정점 쉐이더가 수행하는 세 가지의 변환을 이미지로 표시한 것이다. 오브젝트 공간에서 월드 공간으로 넘어갈 땐 월드 변환, 월드 공간에서 카메라 공간으로 넘어갈 땐 뷰 변환, 카메라 공간에서 클립 공간으로 넘어갈 땐 투영 변환을 수행하게 된다. 위 변환은 정점 쉐이더가 수행하는 연산 중 필수불가결한 변환들이다.
필수 불가결 : 꼭 있어야 하며 없어서는 아니 됨
정점 쉐이더 단계에서 정점에 적용이 될 연산을 사용자가 직접 구현할 수 있게 된다.
👻 노멀의 월드 변환
각자의 오브젝트 공간에서 만들어진 물체를 단일한 월드 공간으로 모으는 것이 월드 변환의 역할이다. 이전에 배웠던 월드 변환은 정점의 위치에 적용되어있었다. 이번 시간에는 노멀에 적용될 월드 변환에 대해 알아볼 것이다.
정점의 위치에 적용했던 월드 변환 적용 방법을 노멀에 적용해도 결과가 오차없이 잘 나올 수 있는지 생각해볼 수 있을 것이다. 결과를 먼저 말하자면 노멀에 수직이 아닌 결과가 나오게 된다.
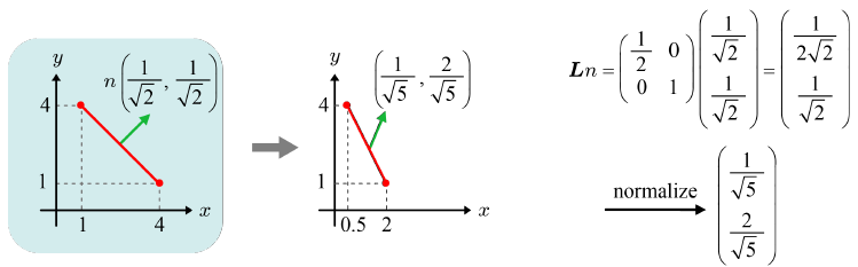
위의 이미지는 3차원 오브젝트 공간의 단면인 xy평면을 보여준다. 빨간 선분은 xy평면에 수직인 삼각형의 단면을, n은 그 삼각형의 노멀을 나타낸다.
여기서
L은 아핀 변환 행렬에서 좌측 상단 누적된 선형 변환 행렬을 의미한다.
여기서 삼각형이 축소확대 행렬 L을 가진다고 가정하고, sx = 0.5, sy = 1이라고 설정하자. L에 의해 변환된 삼각형과 삼각형 노멀은 서로 수직하지 않다는 것을 알 수 있다.
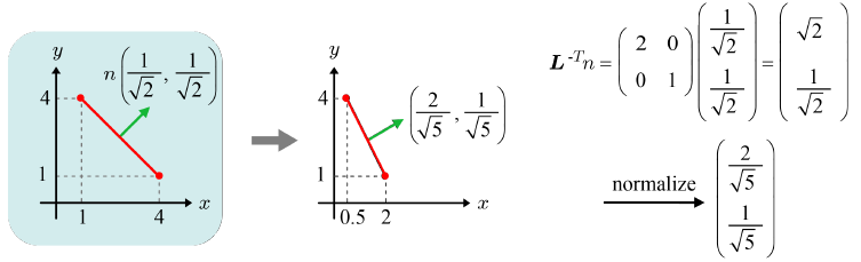
따라서 노멀의 월드 변환을 제대로 적용하려면 L을 바로 적용하는 대신 L의 역전치행렬(Inverse Transpose Matrix)를 적용해야한다. 해당 행렬은 L의 역행렬의 전치행렬을 의미한다. 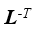
위의 두 이미지에서 노멀을 단위 벡터로 만들기 위해 정규화를 실행하였다.
L을 노멀에 그대로 적용했을 때 문제가 발생했던 것은 L이 비균등 축소확대였기 때문이다. 만약, L이 비균등 축소확대를 포함하지 않는다면 노멀에 그대로 L 을 적용해도 된다. 하지만 알고리즘을 단순화하기 위해 L이 어떠한 성질을 가지건 L의 역전치행렬을 사용하여 노멀의 월드 변환을 수행한다.
💡 기존 아핀 변환은 임의의 포인트
p에 대해Lp+t연산이 수행된다고 공부하였다. 벡터-행렬 곱연산에서 덧셈인 이동t는 무시 가능하다.
👻 뷰 변환
월드 변환이 완료되어 모든 물체가 월드 공간에 모아졌다고 가정하자. 월드 공간의 특정 영역을 스크린에 렌더링하기 위해서는 가상 카메라의 위치와 방향을 설정해야 한다.
🌱 카메라 공간
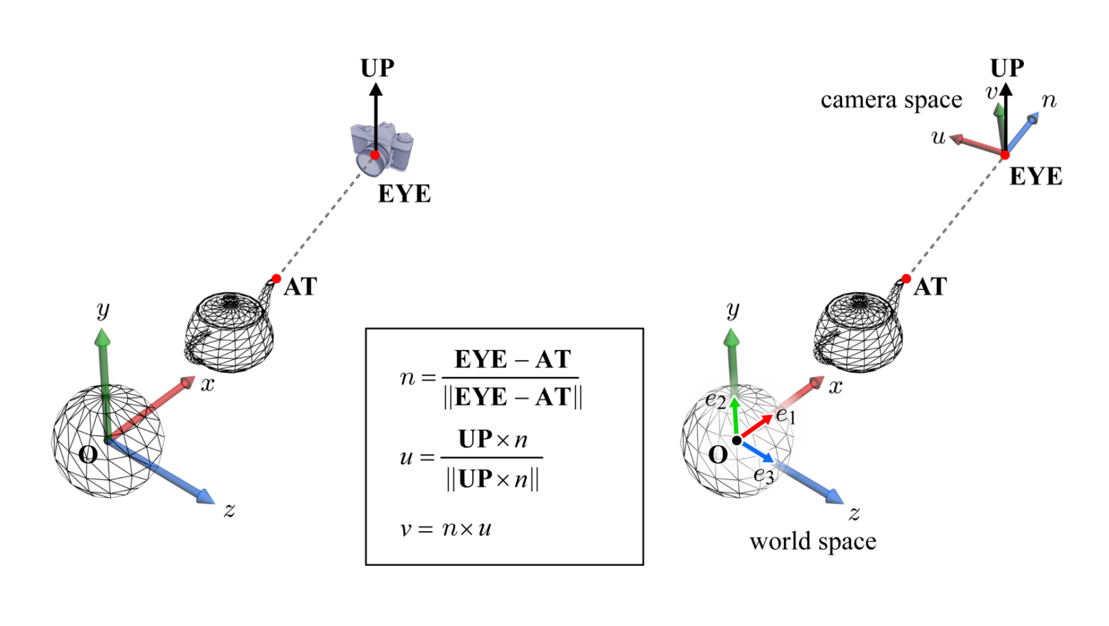
위의 이미지에서 볼 수 있는 것처럼 카메라의 위치와 방향은 EYE, AT, UP 파라미터를 통해 정의된다.
- EYE : 월드 공간에서의 카메라의 위치(시점)
- AT : 월드 공간에서 카메라가 바라보는 기준점(내가 찍고싶은 방향:Look AT)
- UP : 카메라의 상단이 가리키는 방향(내가 찍고싶은 방향의 위쪽 벡터)
이 세 파라미터를 이용해 카메라 공간(Camera Space)이 정의되며 원점은 EYE에 놓여진다.
이전에 알아보았던 오브젝트 공간의 기저처럼, 카메라 공간의 기저도 {u, v, n}으로 표기할 때 다음과 같이 구할 수 있다.
- u :
UP과n의 벡터곱을 정규화하여 얻은 단위 벡터- v :
u와n의 벡터곱- n :
AT과EYE를 잇는 벡터를 정규화하여 얻은 단위 벡터(AttoEye:Eye-At)
위에서 얻은 {u, v, n}은 직교정규 기저이며 카메라 공간을 {u, v, n, EYE}로 표기한다. 월드 공간은 {e₁, e₂, e₃, O}로 표기한다. 여기에서 O는 원점을 의미한다.
💡 카메라 공간에서
EYE,AT,UP이 주어질 때,u,v,n이 정해지는 것만 알면 된다.
🌱 공간 이전과 뷰 행렬
카메라 공간을 지정하게 되면서 월드 공간과 카메라 공간이 생기게 되었다. 하나의 정점은 이 두 공간에서 다른 좌표를 가지게된다.
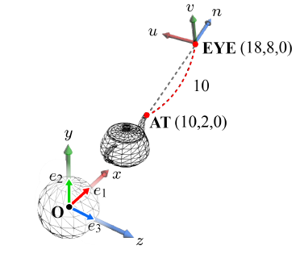
위 이미지에서 EYE의 월드 공간 좌표는 (18, 8, 0)이고, AT의 월드 공간 좌표는 (10, 2, 0)이다. AT은 카메라 공간의 -n축 위에 존재하므로 u와 v는 0이다. 한편 AT과 EYE 사이의 거리는 10이므로 카메라 공간에서의 AT 좌표는 (0, 0, -10)이 된다. 월드 공간 좌표 (10, 2, 0)과 다르게 되는 것이다.
이와 같은 방식으로 월드 공간의 모든 정점들이 카메라 공간으로 재정의되면 렌더링 알고리즘을 설계 구현하는 것이 매우 쉬워진다. 이처럼 하나의 공간에서 정의된 물체를 다른 공간으로 옮기는 것을 일반적으로 공간 이전(Space Change)이라고 부른다.
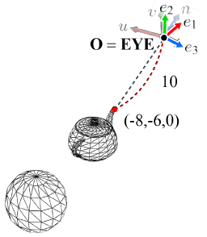
공간 이전의 첫 단계는 EYE를 월드 공간의 원점으로 이동시키는 것이다. 그 다음, {u, v, n}을 {e₁, e₂, e₃}와 일치하도록 회전시키면 된다. 이 과정에서 모든 물체는 카메라 좌표계를 따라 같이 움직인다.
-
이동 후
-
회전(기저 이전) 후
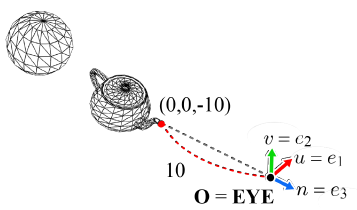
월드 공간에서 카메라 공간으로의 이전을 뷰 변환(View Transform) 혹은 카메라 변환(Camera Transform)이라 부른다.
뷰 변환의 첫 단계인 이동은 변위 벡터 O-EYE 로 정의된다.
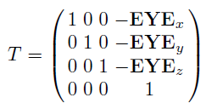
이동이 끝나면 월드 공간과 카메라 공간은 원점을 공유하게 된다. 이제 회전을 통하여 카메라 공간의 기저를 월드 공간의 기저와 포개주려면 다음과 같은 회전 행렬 R을 사용해야한다. 아래의 이미지는 Ru의 회전 행렬을 의미한다.
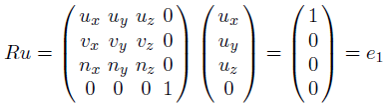
공간 이전을 구성하는 이러한 회전은 기저 이전(Basis Change)이라고 부른다.
뷰 변환은 다음과 같은 뷰 행렬(View Matrix)을 이용하여 수행된다.
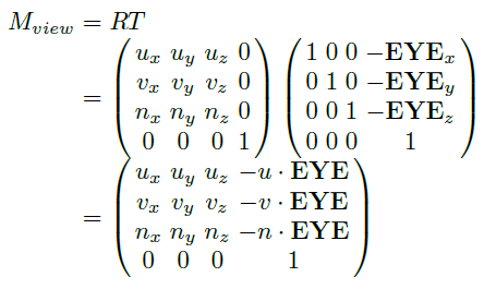
뷰 행렬이 모든 물체에 적용이 되면 월드 공간에 있던 물체들이 카메라 공간에 놓이게 된다고 볼 수 있다.
👻 오른손 좌표계와 왼손 좌표계
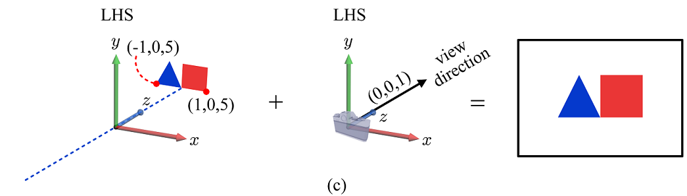
3차원 카테시안 좌표계는 오른손 좌표계(Right-Hand System)와 왼손 좌표계(Left-Hand System)로 나뉜다.
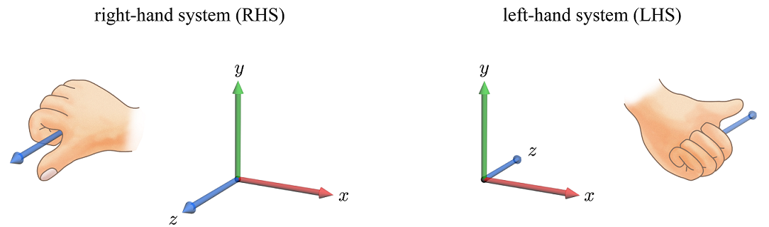
Direct3D는 왼손 좌표계를, OpenGL과 OpenGL ES는 오른손 좌표계를 사용한다.
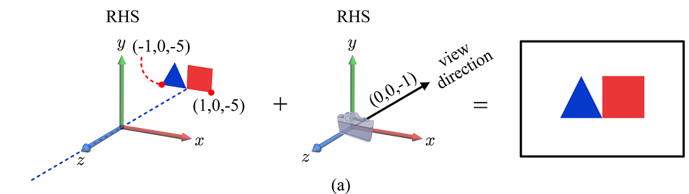
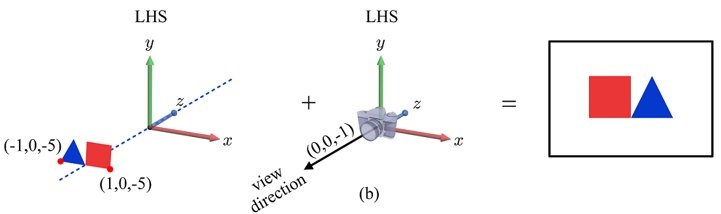
오른손 좌표계는 내가 보는 방향 그대로 즉, 정방향으로 나오지만 왼손 좌표계를 이용하면 거울모드가 적용된 것처럼 반대 방향으로 결과물이 나오게 된다. z좌표의 방향만 반대로 해주면 이러한 현상을 쉽게 해결할 수 있다.
👻 투영 변환
월드 공간에서 정의된 EYE, AT, UP을 카메라의 외부 파라미터라고 본다면, 카메라의 렌즈를 선택하고 줌인/줌아웃을 조절하는 것은 내부 파라미터에 해당한다.
해당 내부 기능은 4가지 파라미터로 설정할 수 있다.
- fovy : y축 기준의 시야각
- aspect : 뷰 볼륨의 종횡비(가로세로 비율. width/height)
- n : 전방 평면(Near Plane)까지의 거리
- f : 후방 평면(Far Plane)까지의 거리
🌱 뷰 프러스텀
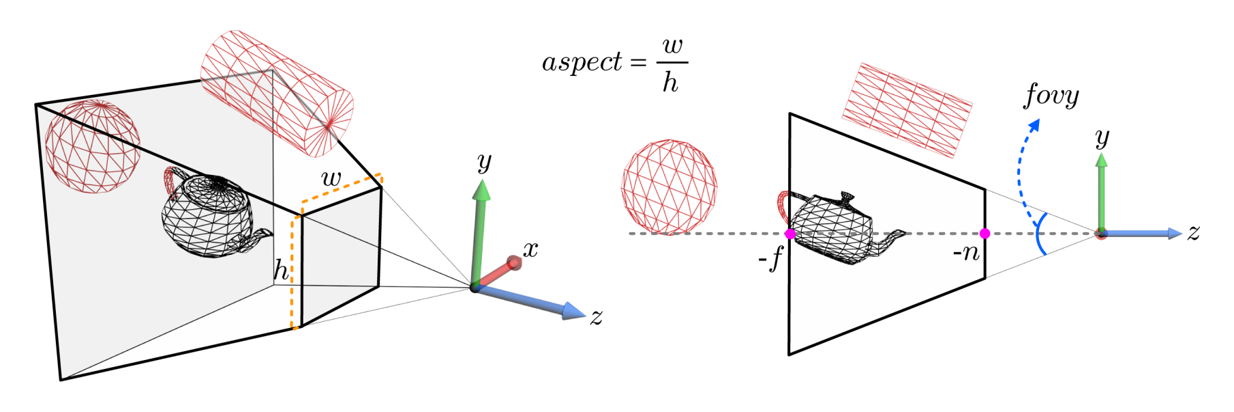
일반적으로 카메라의 시야(Field of View)는 제한되어 있기 때문에 카메라 공간의 모든 물체를 스크린에 담아낼 수 없다. 카메라의 가시 영역을 뷰 볼륨(View Volume)이라 부르는데, 위의 네 파라미터를 사용해 결정된다.
fovy와 aspect에 의해 정의된 무한한 크기의 뷰 볼륨은 z축에 수직인 전방 평면 z = -n과 후방 평면 z = -f에 의해 절단되어 유한한 크기의 뷰 볼륨으로 바뀐다. 이를 뷰 프러스텀(View Frustum) 혹은 절두체(切頭體)라고 부른다.
뷰 프러스텀 바깥에 놓인 물체는 보이지 않는 것으로 처리되므로, 대개 미리 걸러져서 GPU 파이프라인에 들어가지 못하게 한다. 이러한 전처리를 뷰 프러스텀 컬링(View Frustum Culling)이라 부른다.
💡 그래픽스에서 컬링이라 함은, 카메라에 보이지 않아서 최종 영상에 나타날 수 없는 영역을 제거하는 과정을 의미한다.
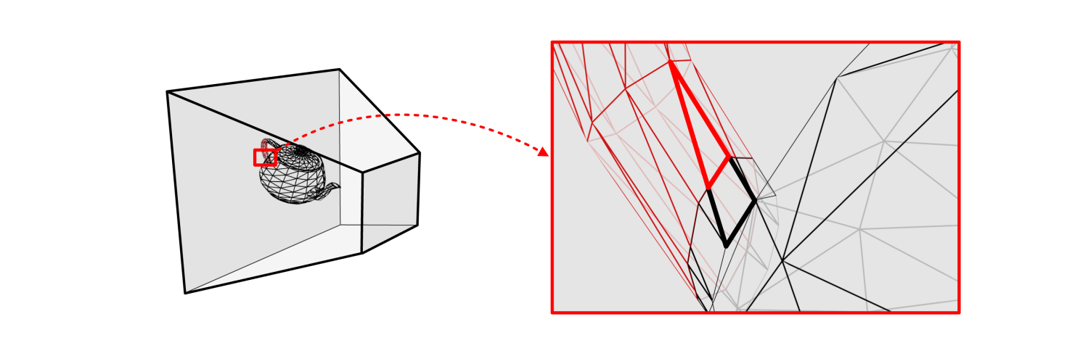
하나의 폴리곤이 뷰 프러스텀과 교차할 경우, 이 폴리곤은 잘라져서 프러스텀 안쪽에 놓인 부분만 GPU 파이프라인의 다음 단계로 넘어가게 된다. 이렇게 폴리곤을 자르는 작업을 클리핑(Clipping)이라 부르는데, 이는 래스터라이저에 의해 수행된다.
💡 뷰 프러스텀 컬링은 프로그래머가 구현해야 하고 CPU에서 실행된다. 반면 클리핑은 래스터라이저 단계 즉, 컴퓨터가 정해둔 함수를 이용하여 실행하는 단계이므로 만약, 컬링이 수행되지 않는다면 클리핑 단계에서 이 작업이 진행되며 폴리곤을 제거하게 될 것이다.
하지만, 이는 GPU에게 부담을 주는 작업이므로, CPU에서 먼저 뷰 프러스텀 컬링을 수행하는 것이 대체로 유리하다.
🌱 투영 행렬
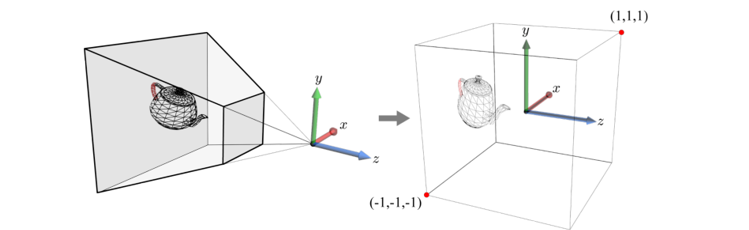
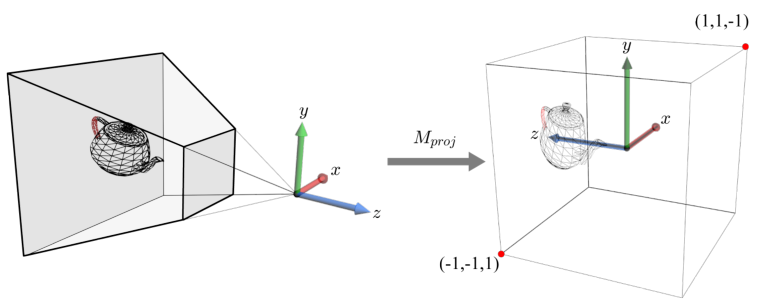
클리핑이 뷰 프러스텀에 겹치는 폴리곤을 자르는 작업이지만, 실제 클리핑은 카메라 공간에서 뷰 프러스텀을 이용해 수행되지 않는다. 카메라로부터 멀어질수록 넓어지는 뷰 프러스텀 공간으로 폴리곤을 자르기는 쉽지 않기 때문이다. 조금 더 폴리곤을 쉽게 자르기 위해서 이러한 뷰 프러스텀을 2 × 2 × 2 크기의 정육면체로 뷰 볼륨으로 변형시킨다. 이를 투영 변환(Projection Transform)이라고 한다. 카메라 공간 물체는 이렇게 투영 변환을 거친 뒤, 정육면체 뷰 볼륨에 대해 클리핑된다. 투영 변환 이후에 물체가 놓이는 공간을 클립 공간(Clip Space)이라고 따로 부른다.
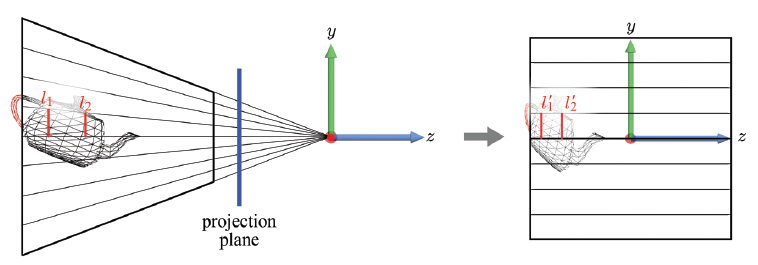
뷰 프러스텀은 원점에 위치한 카메라로 수렴하는 투영선(Projection Lines)들의 집합으로 이해할 수 있다. 뷰 프러스텀과 원점 사이에 놓여 있으면서 z축에 수직인 가상의 투영 평면(Projection Plane)을 생각해 보자. 뷰 프러스텀의 투영선은 투영 평면에 영상을 형성할 것이다(가상의 개념이며 실제론 실체가 없다).
💡 투영 변환이 수행되면서 3차원 공간에서 더 멀리 있는 물체가 작게 보이게 되는데 이것이 바로 원근법이다.
투영 변환의 결과, 모든 투영선들은 서로 평행해져 z축에 나란해지게 되고, 단일한 투영 방향을 가지게 되었다. 주의할 점은, 투영 변환은 3차원 공간 물체를 2차원 투영 평면에 실제로 투영하는 것이 아니라, 3차원 공간 내에서 원근법을 구현한다는 것이다.
투영 변환은 정점 쉐이더가 수행하는 마지막 연산이다. 투영 변환된 물체는 이제 하드웨어로 고정된 래스터라이저로 들어갈 것이다. 래스터라이저는 정육면체 뷰 볼륨을 확대하여 위의 이미지에서 오른쪽에 음영 표시된 면이 스크린에 딱 맞도록 확대할 것이다. 이런 확대는 실제로 물체에 적용되는데, 확대된 물체는 z 축을 따라 스크린에 투영된다.
투영 변환은 강체 변환이 아니다. 외형이 바뀌기 때문이다.
뷰 프러스텀을 2 × 2 × 2 크기의 정육면체로 변형하는 투영 행렬은 다음과 같다.
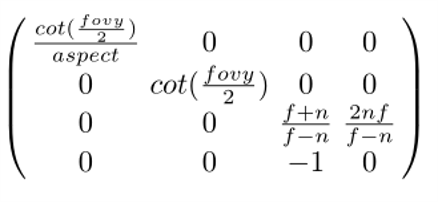
언뜻 보면 복잡해보이지만 잘 살펴보면 방금 알아보았던 내부 기능을 위한 네 개의 뷰 프러스텀 파라미터 fovy, aspect, n, f로만 표현이 되어있다는 것을 알 수 있다. 투영 행렬의 중요한 특징 중 하나는 아핀 변환을 위한 행렬과 달리 마지막 행이 (0 0 0 1)이 아니라는 것이다.
또한, 클립 공간은 오른손 좌표계이지만, 클립 공간의 다음 단계인 래스터라이저는 모든 물체가 왼손 클립 공간에서 정의되어 있다는 가정에서 설계되어있다. 따라서 래스터라이저로 진입하기 위하여 오른손 좌표계를 왼손 좌표계로 변환해야 한다. 이를 위해서는 정점 z 좌표의 부호를 변경하면 된다.
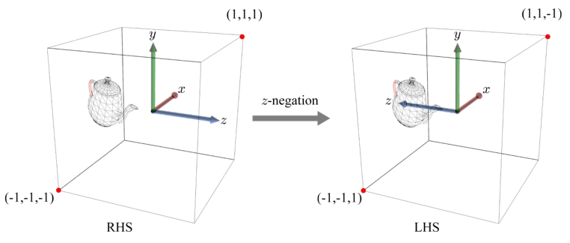
z 좌표를 관리하는 곳은 행렬의 세 번째 행이다. 따라서 M의 세 번째 행의 모든 원소의 부호를 바꾸면 좌표계를 바꿀 수 있다.
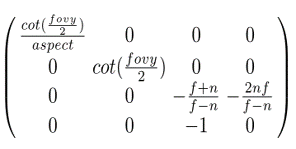
위의 투영 행렬을 사용하면 오른손 카메라 공간에서 정의된 정점을 왼손 클립 공간으로 옮길 수 있게 된다.
👻 글을 마치며
이번 시간에는 정점 처리(정점 쉐이더) 단계에 대해 어떤 식으로 데이터 처리가 이루어지는지 알아보았다. 굉장히 내용이 많고 복잡해서 복습을 한 번 더 했다. 그 결과 어떤식으로 컴퓨터가 데이터를 입력받고 정점 계산을 하는지 알 수 있었다. 애매한 게 거의 대부분의 계산이 행렬, 벡터를 사용하는 것이다보니 외워야 할 변환 행렬이 좀 있는 것 같다. 과정만 알면 자연스럽게 유도가 될 수 있을 것 같은데 아직까진 눈에 익지 않는 것 같다. 😂 익을 때까지 복습해야겠다.
출처
한정현 컴퓨터 그래픽스 강의 (5장-정점 처리)
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment