[Computer Graphics] #16. 전역 조명과 텍스처링
👻 전역 조명과 텍스처링
조명 모델은 일반적으로 지역 조명(Local Illumination)과 전역 조명(Global Illumination) 두 가지로 구분된다. 앞서 배웠던 퐁 모델은 지역 조명 모델인데, 이는 조명 대상인 물체의 표면 재질과 광원의 속성만 이용해 해당 표면의 색상을 결정할 뿐, 같은 공간에 있는 다른 물체는 고려하지 않는다.
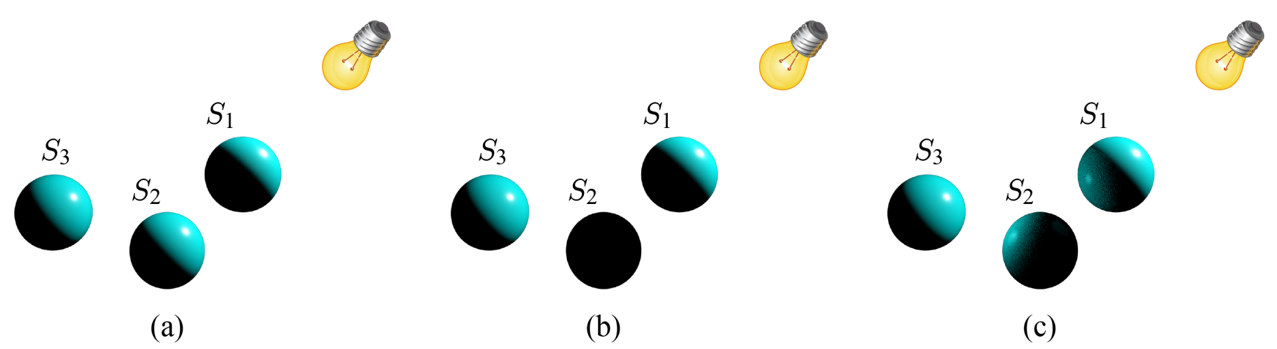
위 이미지에서 S1과 S2가 일직선상에 있다고 가정할 때, S2는 S1에 가려져 빛을 받지 않아야 하지만 그림-(a)의 경우 모두 동일한 방향으로 빛을 받는 것을 알 수 있다. 이 것은 퐁 모델을 적용시킨 라이팅 결과이며 이는 물리학적으로 올바르지 않은 모델이다. 그림-(b)의 경우 S2가 빛을 아예 받지 못하는데, 이것 또한 잘못된 결과이다. 올바른 결과는 그림-(c)이며 이는 장면의 모든 물체를 잠재적인 광원으로 취급하여 반사된 빛이 적용된 결과이다.
👻 전역 조명 모델
컴퓨터 그래픽스 역사 초기에 제안된 전역 조명 기법은 광선 추적법(Ray Tracing)과 래디오시티(Radiosity)인데, 이들은 현재에도 여전히 널리 사용되고 있다. 이 두 기법에 대해 알아보자.
🌱 광선 추적법
뷰 프러스텀에서, 투영선의 개수는 스크린 영상의 해상도와 같고, 투영선 하나가 픽셀 하나의 색상을 결정한다. 광선 추적법 알고리즘에서는 각 투영선 반대 방향으로 광선을 발사한 뒤 이를 추적하여 해당 투영선을 따라 들어오게 될 색상을 계산한다. 이것이 바로 픽셀 색상이 되며 이렇게 투영선 역방향으로 발사되는 광선을 1차 광선(Primary Ray)이라 부른다.
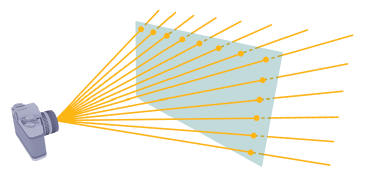
이러한 1차 광선이 어떤 물체와 부딪히면 우선 그 교차점이 그림자 안에 있는가를 검사한다. 이를 위해 그림자 광선(Shadow Ray)이라는 이름의 2차 광선(Secondary Ray)을 각 광원을 향해 발사한다.
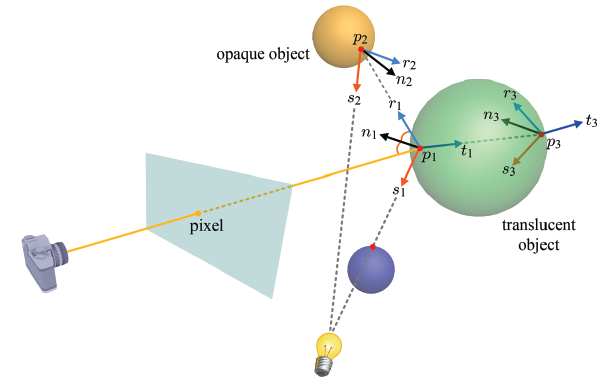
위 이미지에서 1차 광선은 커다란 반투명 구와 p1에서 교차한다. 여기서 광원 방향으로 그림자 광선 s1이 발사되고, 또 노멀을 기준으로 동일한 각을 가지는 반사 광선(Reflection Ray)과 반투명한 물체와 부딪힐 때 발생하는 굴절 광선(Refraction Ray 혹은 Transmitted Ray)도 발사된다. 물론 불투명한 물체에 부딪히면 굴절 광선은 발사되지 않는다.
💡 반사 광선과 굴절 광선 모두 2차 광선에 속한다.
이렇게 광선 추적법은 재귀적인 알고리즘을 수행하며 광선 트리(Ray Tree)로 설명할 수 있다.
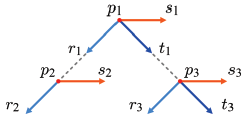
이 광선 트리는 반사/굴절 광선이 어떤 물체에도 부딪히지 않고 장면을 벗어날 때까지 또는 미리 정의된 재귀 단계에 도달할 때까지 확장된다.
광선 트리의 노드 p3를 생각해 보자. r3를 추적해서 얻은 색상은 p3의 스페큘러 계수와 곱해지고, t3를 추적해서 얻은 색상은 p3의 투과율(Transmission Coefficient)과 곱해진다. 이 둘은 s3를 통해 계산된 직접 조명 색상에 더해지고, 그 결과는 부모 노드인 p1으로 전달된다. 이와 같은 작업이 광선 트리의 모든 노드에서 재귀적으로 진행되면 최종적으로 루트 노드에서의 색상을 얻을 수 있다. 이것이 바로 1차 광선이 부딪힌 점의 색상이다.
이러한 광선 추적법으로 생성한 영상의 예시는 아래와 같다.

💡 굴절 광선 벡터를 계산하는 방법은 스넬의 법칙(Snell’s Law)을 이용한다.
🌱 래디오시티 알고리즘
래디오시티 알고리즘은 디퓨즈 표면을 가진 물체들 사이에서 반사되는 빛을 계산한다. 고로 장면을 구성하는 모든 표면은 광원과 같은 역할을 한다.
래디오시티를 이용한 전역 조명을 구현하기 위해서는 먼저 장면 내 존재하는 모든 표면을 잘게 나눠 패치(Patch)들을 만든다. 그 다음, 패치 사이의 형태 인자(Form Factor)를 계산한다. 이는 한 패치에서 다른 패치가 얼마만큼 보이는지 계산한 것인데, 두 패치 간 거리 및 각 패치의 방향에 좌우된다. 만약 패치 간 거리가 크고, 패치가 서로 정면을 보지 않고 기울어져 있다면 형태 인자는 작은 값을 가질 것이다.
한 패치의 래디오시티는 그 패치로부터 나오는 빛의 속도라고 정의되는데, 그 패치가 직접 빛을 발산하는 속도에 그 패치가 빛을 반사하는 속도를 더한 것으로 결정된다.
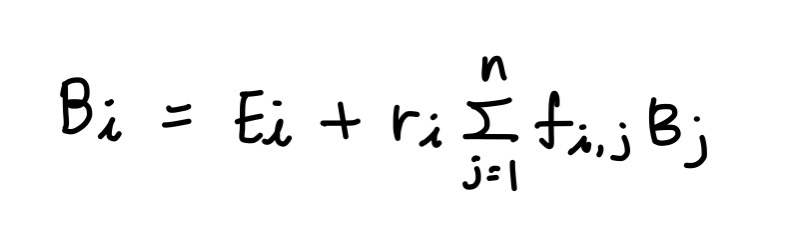
여기에서 B는 각각 패치 p의 래디오시티이고, E는 패치 p의 초기 래디오시티, r은 패치 p의 반사 계수, f는 형태 인자이다. 광원이 아닌 경우, E는 0이 되며 시그마 식은 패치 p에 들어오는 빛(Irradiance)을 말한다. 이를 고쳐쓰면 다음과 같다.
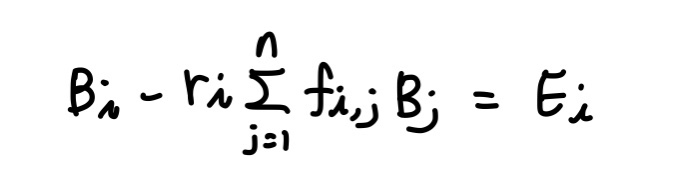
장면의 모든 패치에 위 식을 적용하면 다음과 같은 선형 시스템(Linear System)을 얻을 수 있다.
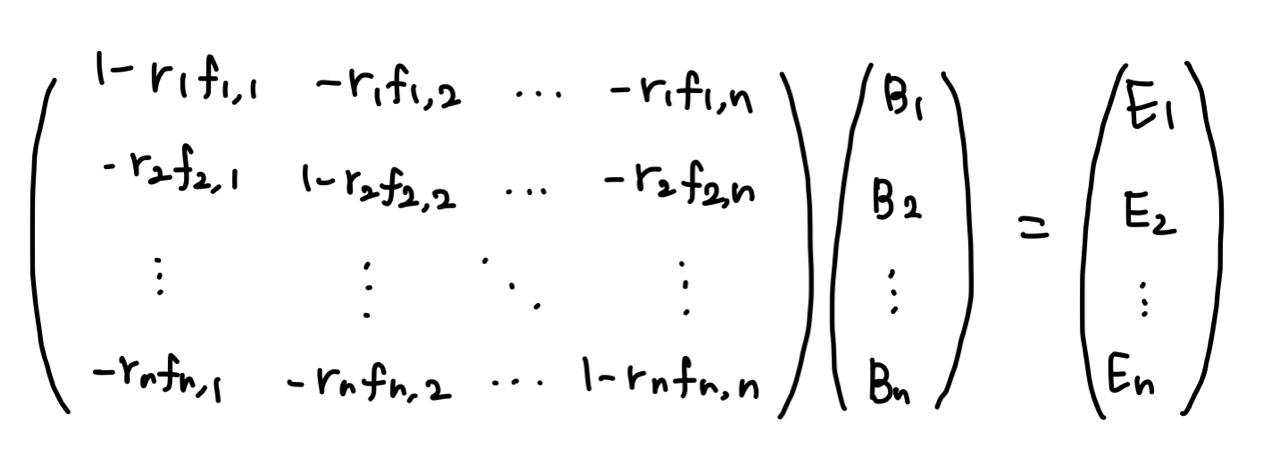
이를 풀면 모든 패치의 래디오시티를 구할 수 있다.
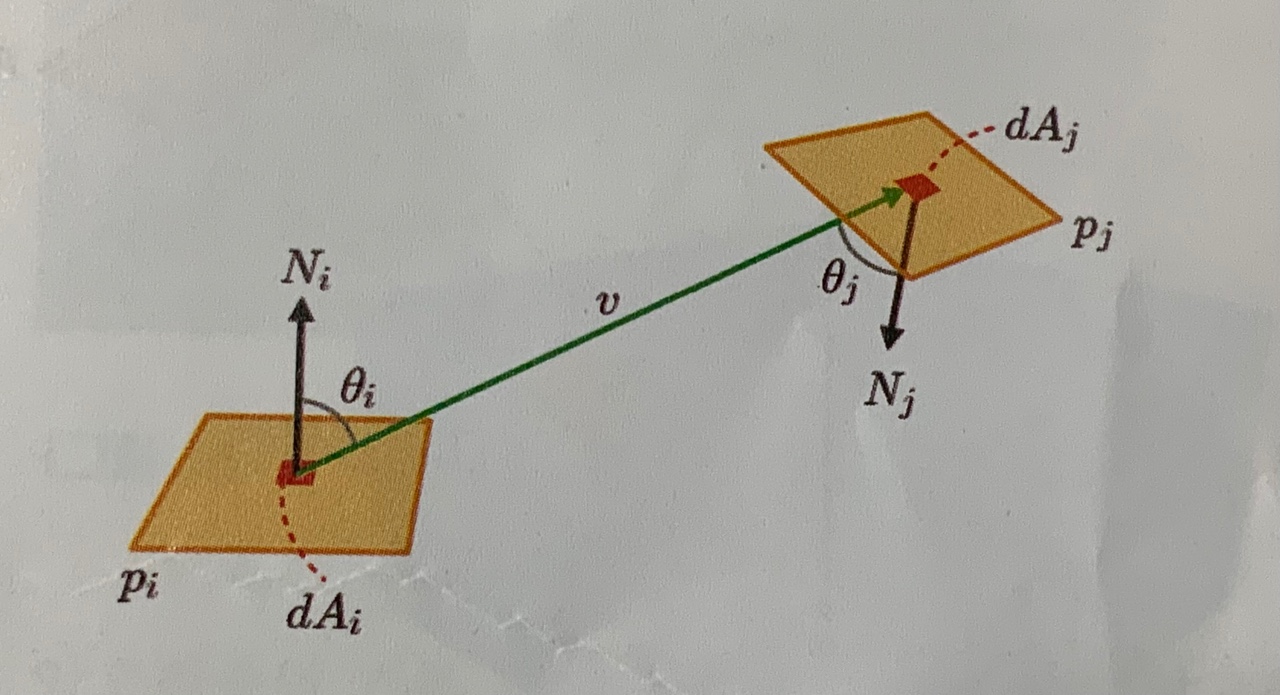
형태 인자에 대해 조금 더 논의해 보자면, 위 그림의 두 패치 pi와 pj 각각은 미분 면적 dA와 표면 노멀 N을 가지는데, 면적을 잇는 벡터를 v, N과 v사이의 각도를 θ로 표기하면 면적 간 형태 인자는 다음과 같이 정의된다.
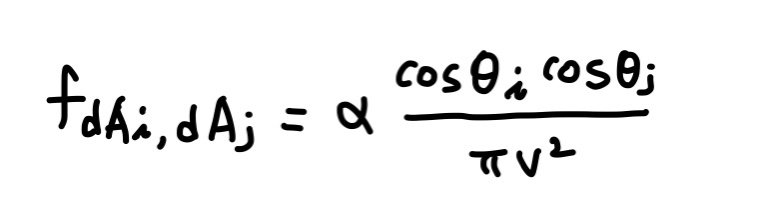
여기에서 α는 면적 간 가시성(Visibility)을 의미한다. 만약 dAi에서 dAj를 볼 수 있다면 α는 1이고 그렇지 않으면 0이다. 또한 dAi에서 dAj를 볼 수 있다면 dAj에서도 dAi를 볼 수 있다.
위 식은 점과 점 사이의 형태 인자를 정의하므로, 두 패치 사이의 형태 인자를 계산하기 위해서는 위 식을 적분해야 한다. 그런데, 한 패치의 모든 점에서 래디오시티가 일정하다고 가정하면, 패치와 패치 간 형태 인자 계산은 점과 패치 간 형태 인자 계산으로 대체될 수 있다. 패치 pi의 대표점을 q라 할 때, 다음과 같이 q에 반구(Hemisphere)를 올려놓아 형태 인자를 계산할 수 있다.
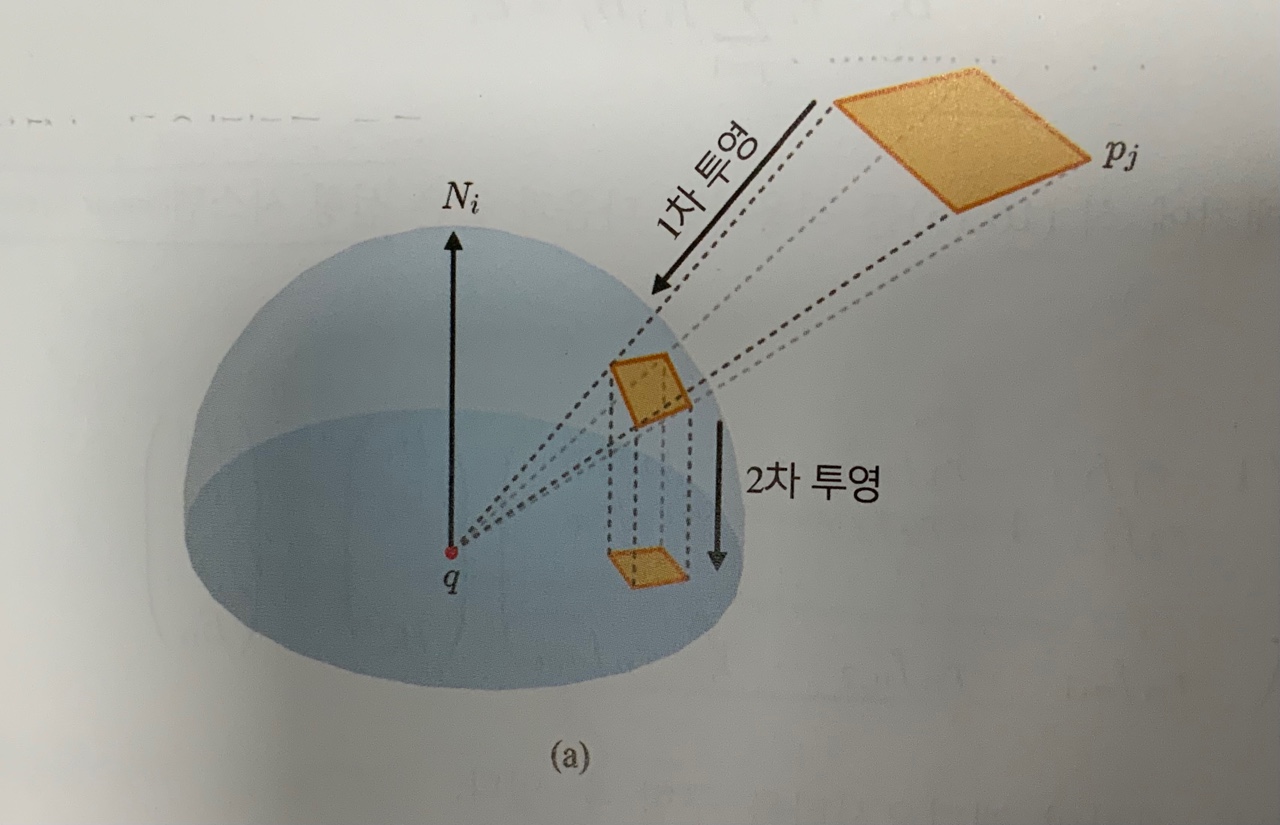
형태 인자를 계산하기 위해서는 pj를 먼저 반구 표면에 투영하고 그 결과를 다시 반구 바닥에 투영한다. 이렇게 투영된 면적이 반구의 바닥면에서 차지하는 비율로 형태 인자를 결정할 수 있다.
반구를 반정육면체(Hemicube)로 대체하면 래디오시티 알고리즘의 최적화가 가능하다.
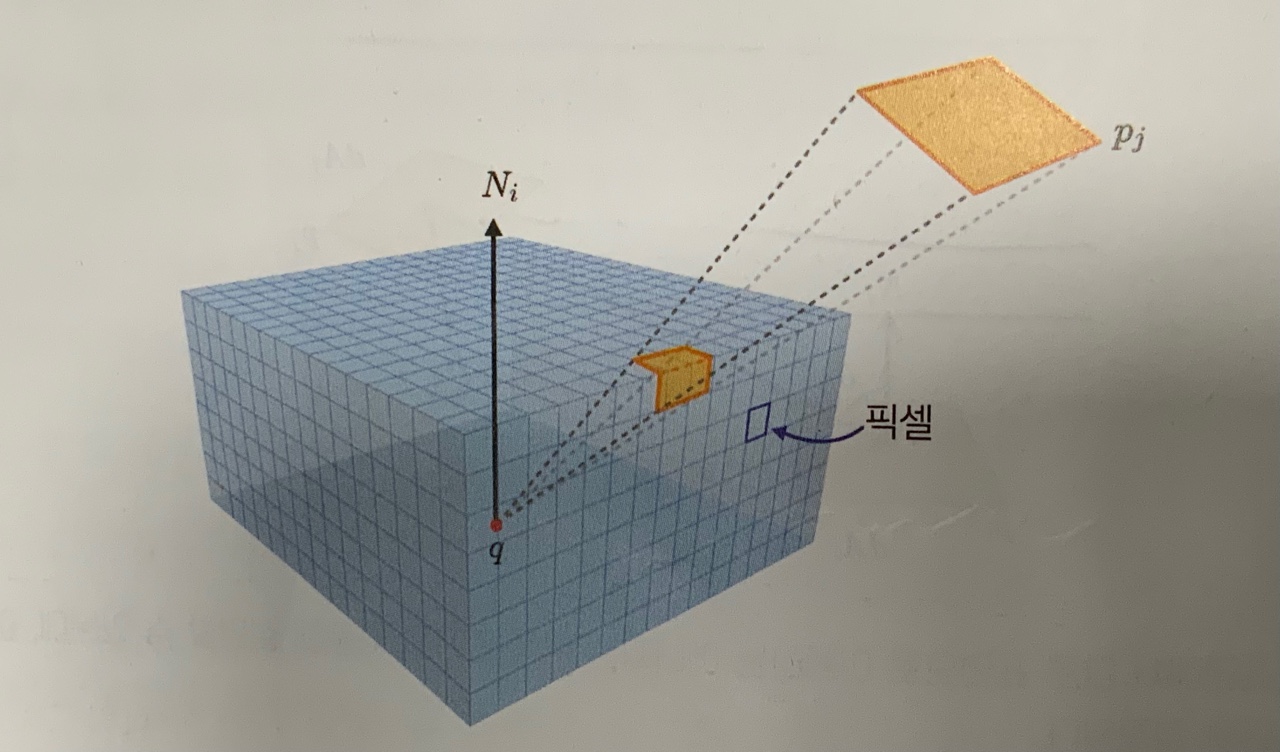
노멀 축에 가까이 놓일수록 모서리에 놓인 픽셀보다 큰 형태 인자를 가지게 된다. 이러한 픽셀 별 형태 인자는 미리 계산된다. 반정육면체의 경우 pj가 투영된 영역에 속하는 픽셀들의 형태 인자들의 합으로 정의된다. z-버퍼링 알고리즘을 사용하면 q에서의 pj 가시성도 동시에 처리할 수 있다.

하지만 래디오시티 알고리즘은 실시간에 구현하기에 연산량이 너무 많기 때문에, 보통 전처리 단계에서 이를 실행하여 텍스처에 저장한 후, 런타임에 이 텍스처를 사용한다. 이러한 텍스처를 라이트맵(Light Map)이라고 부른다.
👻 라이트 매핑
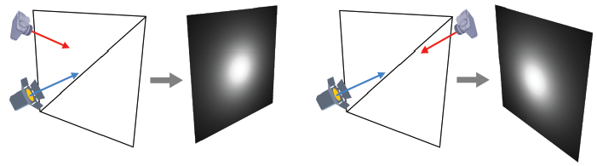
위 이미지는 사각형 벽면을 스포트라이트(Spot Light)가 비추고 있는 상태에서 카메라가 왼쪽에서 오른쪽으로 움직이는 것을 보여준다. 벽이 흰색 디퓨즈 표면이고 광원 역시 흰색이라고 가정하면, 카메라에 잡히는 벽의 색상은 회색조일 것이다. 이는 바로 디퓨즈 반사 색상이고, 이는 카메라 위치에 관계없이 일정하다.
이렇게 물체와 광원이 모두 고정되어 있다면 색상은 변하지 않으므로 이를 미리 계산하여 텍스처에 저장할 수 있다. 이 텍스처를 라이트맵(Light Map)이라 부른다.

런타임에는 라이트맵에서 퐁 모델의 디퓨즈 항의 빛 정보(max(n·l, 0)sd)를, 이미지 텍스처에서 디퓨즈 계수 md를 읽어와 둘을 결합한다. 이러한 기법을 라이트 매핑(Light Mapping)이라고 부르며, 런타임에 별다른 계산을 하지 않으므로 런타임 성능이 향상된다.
한편, 라이트맵은 대체로 이미지 텍스처보다 낮은 해상도를 가진다. 물체 표면에서 디퓨즈 색상의 변화는 대체로 완만하므로 저해상도로 넓은 표면 영역을 표현하는 것이 가능하기 때문이다.
💡 대부분의 라이트맵은 래디오시티 알고리즘을 통해 만들어진다.
라이트 매핑은 런타임 성능만 향상시키는 게 아니다. 라이트맵은 전처리 단계에서 생성되므로 충분한 시간을 가지고 만들 수 있다. 따라서 연산량이 많은 고급 조명 모델을 사용할 수 있다. 따라서 라이트 매핑된 장면은 지역 조명으로 처리된 것보다 높은 품질의 영상을 보여준다.
라이트맵을 만드는 방식은 노멀맵 제작 방식과 유사하다. 우선 라이트 매핑이 적용될 표면을 파라미터화한 다음, 텍스처 공간에서 스캔 전환한다. 이렇게 생성된 각 텍셀에 해당하는 물체 표면의 점을 구하고 여기에 들어오는 빛을 계산하여 텍스처에 저장한다.
👻 환경 매핑

위 이미지와 같이 주변 환경을 반사하는 매끄러운 물체를 렌더링하는 기법이 환경 매핑(Environment Mapping)이다. 이를 위해 첫 번째로 해야 할 일은 환경맵(Environment Map)이라고 불리는 텍스처에 주변 환경의 영상을 담는 것이다.
🌱 큐브 매핑
가장 많이 쓰이는 환경맵은 큐브맵(Cube Map)이다.

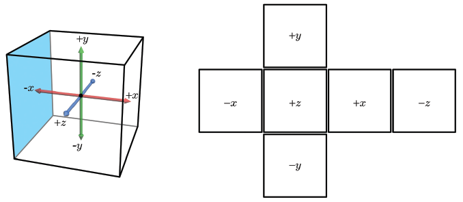
위 이미지는 가상의 정육면체, 그리고 그 중심에 위치한 카메라를 보여준다. 이 정육면체의 여섯 개 면 각각을 향해서 수직과 수평 방향으로 모두 90˚의 시야각(Field of View)을 설정해 사진을 찍거나 렌더링을 수행하면 여섯 개의 정사각형 이미지를 얻을 수 있다. 이를 정육면체에 붙여 놓은 것을 큐브맵이라 볼 수 있다.
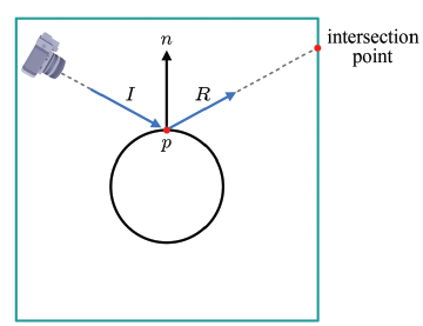
큐브 매핑 구현은 쉽다. 위 이미지는 정사각형 단면으로 그려진 큐브맵 내의 카메라와 공 모양의 물체를 보여준다. 개념적으로 큐브맵은 물체를 감싸는 것으로 간주할 수 있고, 카메라로부터 p를 향해 광선 I를 발사하고 이를 추적한다. I는 p의 표면 노멀 n을 기준으로 반사되어 R이라는 벡터를 결정한다.
R = I - 2n(n·l)
반사 벡터 R은 큐브맵의 한 면과 교차하는데, 이 교차점을 이용해 해당 면의 이미지 텍스처를 필터링한다. 이 결과가 바로 p에서 반사되는 색상을 결정한다. 이러한 큐브 매핑은 간략화된 광선 추적법이라 부를 수 있는데, 2차 광선 중 반사 광선만 추적이 되고 재귀적인 과정도 거치지 않기 때문이다.
🌱 큐브 매핑을 위한 GL 프로그램과 쉐이더
큐브 매핑은 CG에서 널리 쓰이므로 GL도 이를 지원한다.
다음은 큐브맵 생성을 위한 GL 프로그램이다.
TexData texData;
GLuint texture;
glGenTextures(1, &texture);
glBindTexture(GL_TEXTURE_CUBE_MAP, texture);
for (unsigned int i = 0; i < 6; i++)
glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGBA,
texData.width, texData.height, 0, GL_RGBA, GL_UNSIGNED_BYTE,
texData.texels.data() + texData.texels.size() * i / 6);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
큐브맵도 텍스처의 한 종류이기 때문에 모든 텍스처 오브젝트 생성에 필요한 glGenTextures와 glBindTexture가 호출된다. 그 다음 texData에 저장된 여섯 개의 이미지를 큐브맵 텍스처의 여섯 면에 하나씩 채ㅔ워가기 위하여 glTexImage2D를 여섯 번 호출할 것이다.
💡 큐브맵의 여섯 개 이미지 각각은 자신을 가리키는 좌표축의 이름을 부여받는다.
- 기본 형식 :
GL_TEXTURE_CUBE_MAP_*- ‘*‘에 들어올 수 있는 것
POSITIVE_X: +xNEGATIVE_X: -xPOSITIVE_Y: +yNEGATIVE_Y: -yPOSITIVE_Z: +zNEGATIVE_Z: -z- 이는 1씩 증가할 때마다 위의 순서를 따른다.
다음은 큐브 매핑을 위한 정점 쉐이더와 프래그먼트 쉐이더이다.
- 큐브 매핑을 위한 정점 쉐이더
#version 300 es
uniform mat4 worldMat, viewMat, projMat;
uniform vec3 eyePos;
layout(location = 0) in vec3 position;
layout(location = 1) in vec3 normal;
out vec3 v_normal, v_view;
void main() {
v_normal = normalize(transpose(inverse(mat3(worldMat))) * normal);
vec3 worldPos = (worldMat * vec4(position, 1.0)).xyz;
v_view = normalize(eyePos - worldPos);
gl_Position = projMat * viewMat * vec4(worldPos, 1.0);
}
- 큐브 매핑을 위한 프래그먼트 쉐이더
#version 300 es
precision mediump float;
uniform samplerCube cubeMap;
in vec3 v_normal, v_view;
layout(location = 0) out vec4 fragColor;
void main() {
vec3 normal = normalize(v_normal);
vec3 view = normalize(v_view);
vec3 refl = 2.0 * normal * dot(normal, view) - view;
fragColor = texture(cubeMap, refl);
}
큐브맵을 나타내는 유니폼 cubeMap은 samplerCube 타입으로 정의되었으며 내장 함수 texture는 refl을 이용해 cubeMap에 접근한다. 여기서 한 가지 주의해야 할 점은 view의 방향이다(I = -view).
환경 매핑 구현 방법은 매우 간단하지만 그 결과는 훌륭하다. 하지만 이 방법이 모든 문제를 해결해주진 않는다. 다시 위로 올라가 주전자의 손잡이를 보면 주전자 몸체에 반사되지 않는 것을 알 수 없다. 물체는 자기 자신을 반사하지 못하기 때문에 이런 문제가 발생하게 된다.
👻 앰비언트 오클루전
퐁 모델의 앰비언트 항은 간접 조명을 담당하는데, 표면상의 한 점을 향해 모든 방향에서 고루 앰비언트 빛이 들어온다고 가정한다. 하지만 특정한 방향으로는 앰비언트 빛이 들어올 수 없는 경우가 있다.
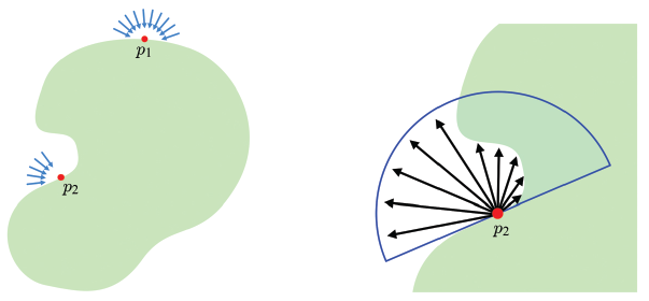
위 이미지에서 p1과 p2를 비교해 보자. p1으로 들어오는 앰비언트 빛은 아무 방해를 받지 않지만, p2로 들어오는 앰비언트 빛은 물체의 다른 부분에 일부 가려진다.
앰비언트 빛이 가려지는 정도 즉 차폐도(遮蔽度, Occlusion Degree)를 계산하고 이를 이용해 앰비언트 항 sa ⊗ ma의 값을 조절하는 기법을 앰비언트 오클루전(Ambient Occlusion)이라 한다.
위 이미지에 적용해보면 p2의 차폐도는 p1보다 크므로 앰비언트 빛을 더 적게 받고, 결국 앰비언트 반사를 더 적게 할 것이다.
오른쪽 이미지에 보인 것처럼 p2에 반구를 놓아보자. 반구의 중심축은 p2의 표면 노멀과 같다. 차폐도 계산을 위해 반구 표면을 균일하게 샘플링하고 p2에서 샘플점으로 광선을 발사한다. 광선 중 일부는 물체와 충돌할 것이다. 발사된 모든 광선 중 이렇게 물체와 부딪히는 광선이 차지하는 비율이 차폐도이다.
하지만 이렇게 광선을 사용하면 비용이 많이 든다.
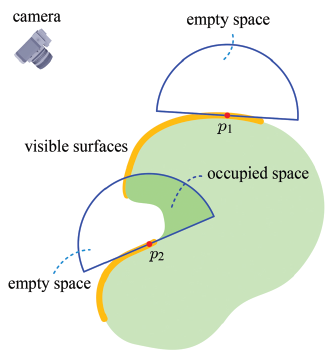
위 이미지를 보면, p2에 놓인 반구는 빈 공간과 채워진 공간으로 구분될 수 있고, 차폐도는 전체 반구 공간에서 채워진 공간이 차지하는 비율로 근사될 수 있다. 부피 계산은 어려우므로 고르게 샘플 점을 뿌리고 이들이 빈 공간에 있는지 아니면 채워진 공간에 있는지 검사하는 방법을 생각할 수 있다.
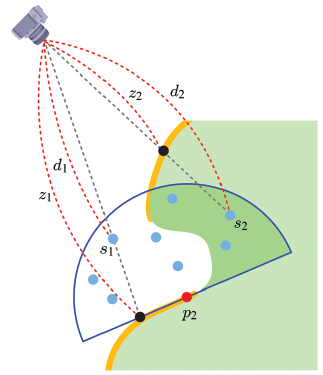
이를 효율적으로 구현하기 위해서는 먼저 렌더링할 장면의 깊이맵을 생성한다. 위 이미지에서 물체 표면의 굵은 선은 카메라가 볼 수 있는 부분을 나타내는데, 이 표면의 스크린 공간 깊이값이 깊이맵에 저장된다. 이를 샘플 점과의 거리와 비교하여 해당 점이 속한 공간을 결정한다. 카메라와 샘플점과의 거리가 깊이값보다 크면 채워진 공간, 작거나 같다면 빈 공간에 속한다고 볼 수 있다.

위 이미지는 퐁 모델의 앰비언트 항만을 사용한 경우와 앰비언트 오클루전을 사용한 경우의 렌더링 결과를 비교한다. 앰비언트 오클루전이 물체 표면의 음영을 얼마나 잘 표현하는지 확인할 수 있다. 그러나 앰비언트 오클루전은 스크린 공간에서 근사적인 계산을 수행하므로 몇 가지 문제점을 가지고 있다. 예를 들어, 뷰 프러스텀 밖에 위치한 물체는 고려하지 않기 때문에 오류가 발생할 수 있다.
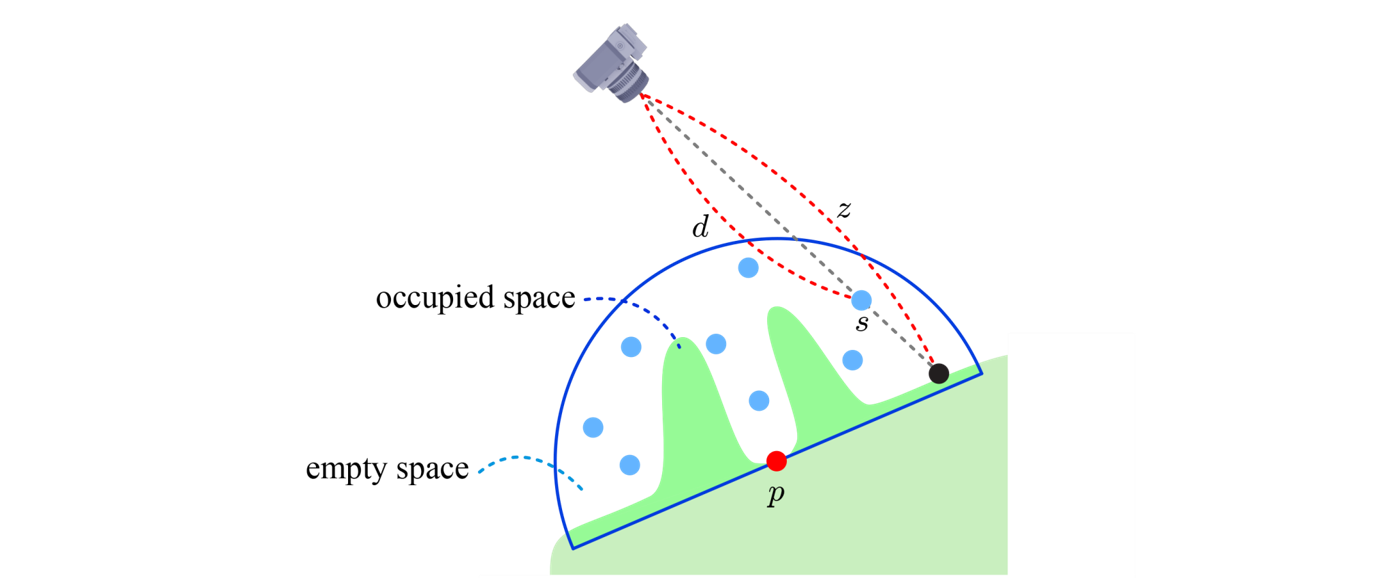
위 이미지는 이런 경우가 아니더라도 차폐도 계산에 오류가 발생할 수 있음을 보여준다. 하지만 다행스럽게도 이런 오류는 일반 사용자들 눈에는 거의 발견되지 않기 때문에 앰비언트 오클루전 알고리즘은 게임 등에서 널리 사용된다.
👻 글을 마치며
이번 시간에는 전역 조명과 텍스처링에 대해 알아보았다. 뭔가 단어가 확 와닿지 않아서 개념 정리하기 쉽지 않았는데 결국 앞서 배웠던 기법들의 심화 과정으로 생각하면 개념 확장 정도로 생각할 수 있겠다. 깊게 알수록 복잡해지는 그래픽스.. 좋은데 싫다…😞
출처
한정현 컴퓨터 그래픽스 강의 (16장-전역 조명과 텍스처링)
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment