[Computer Graphics] #18. GPU 테셀레이션

May 9, 2023

👻 GPU 테셀레이션

GPU 파이프라인이 처리하는 기하적인 개체를 프리미티브(Primitive)라고 하는데, 하나의 프리미티브를 여러 개의 작은 프리미티브로 잘게 나누는 것을 테셀레이션(Tessellation)이라고 한다. GPU가 처리하는 과정에서 이루어지는 테셀레이션에 대해 알아보자.

Alt Text

OpenGL ES 3.2는 GPU 테셀레이션을 지원한다. 이를 위해서 테셀레이션 컨트롤 쉐이더(Tessellation Control Shader; 이하 컨트롤 쉐이더로 약칭)와 테셀레이션 생성 쉐이더(Tessellation Evaluation Shader; 이하 생성 쉐이더로 약칭)가 추가되었다. 또한 두 쉐이더 사이에는 하드웨어로 고정된(Hardwired) 단계인 테셀레이션 프리미티브 생성기(Tessellation Primitive Generator; 이하 테셀레이터로 약칭)가 놓인다. 이러한 과정은 위 파이프라인 이미지에서 확인 가능하다.

GPU 테셀레이션을 사용하면 매우 복잡한 표면을 실시간에 생성할 수 있는데, 대표적인 테셀레이션 기법인 변위 매핑(Displacement Mapping)과 PN-삼각형에 대해 알아보자.

👻 변위 매핑

이전에 알아보았던 노멀 매핑은 기초 표면(Base Surface) 자체를 오돌토돌하게 바꾸는 게 아니라 참조 표면(Reference Surface)의 노멀을 사용하여 오돌토돌한 표면을 ‘흉내’낸 것이었다. 하지만, 변위 매핑은 기초 표면을 고해상도 메시로 바꾼 후 그 메시의 정점 위치를 옮겨서(Displace) 실제로 오돌토돌한 메시를 만든다.

🌱 변위 매핑을 위한 GPU 테셀레이션

변위 매핑 구현을 위해서는 컨트롤 쉐이더, 테셀레이터, 생성 쉐이더가 순차적으로 작업을 수행한다. 컨트롤 쉐이더의 입력은 패치(Patch)라고 부르는데, 이는 GL 3.2에 새로 추가된 프리미티브 타입으로, 사각형(Quad)과 삼각형 중 하나이다. 아래의 흐름도에서 컨트롤 쉐이더는 사각형 패치를 입력으로 받아서, 이를 그대로 생성 쉐이더에게 넘겨주는 과정을 보여준다.

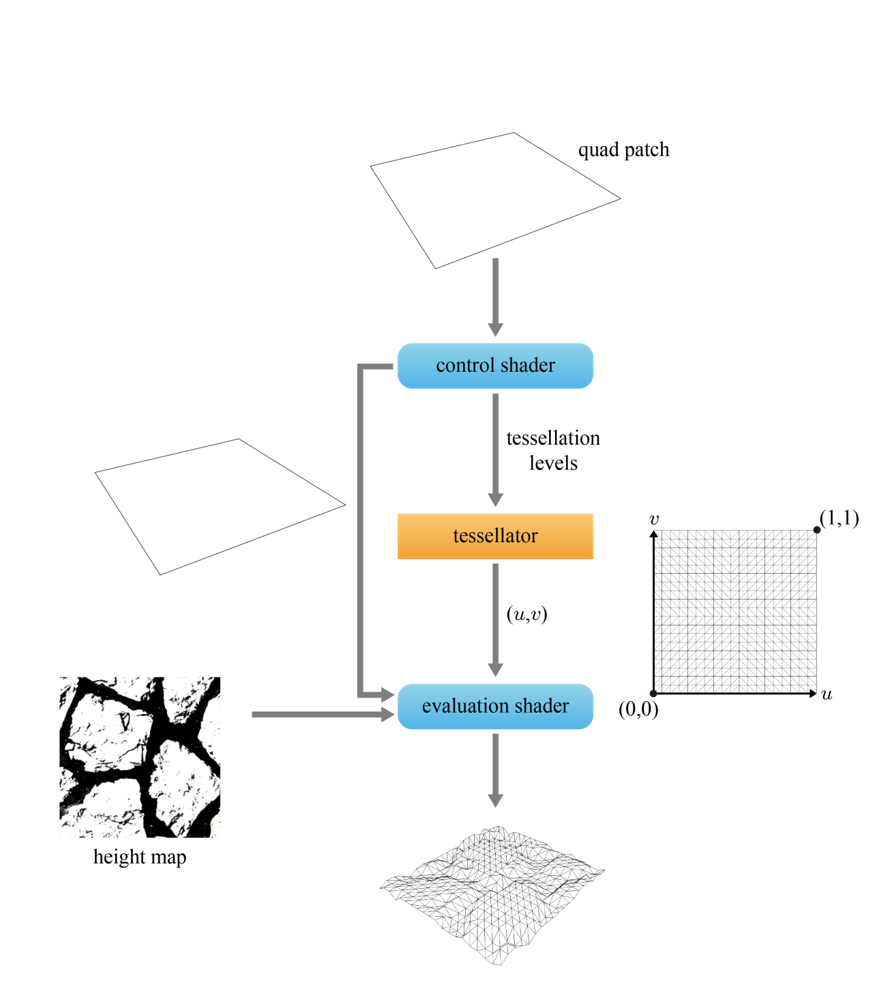
Alt Text

컨트롤 쉐이더는 이 사각형 패치를 얼마나 잘게 나눌지 결정해서 테셀레이터에게 알려줘야 한다. 이를 테셀레이션 레벨이라고 하며, 테셀레이터는 컨트롤 쉐이더가 지정해주는 대로 사각형 패치의 정의역(Domain)을 잘게 나눠 2차원 메시를 구성한다. 이러한 2차원 메시는 정점마다 (u, v) 좌표가 할당된다.

2차원 메시의 각 정점에 대해 생성 쉐이더가 한 번 실행되는데, 여러 개의 정점이 여러 개의 생성 쉐이더에 의해 병렬 처리된다.

💡 생성 쉐이더의 처리 과정

컨트롤 쉐이더가 건네준 사각형 패치를 겹선형 패치로 간주하고 테셀레이터가 건네준 (u, v)를 사용해서 사각형 패치의 한 점을 생성한다.

GL 프로그램은 하이트맵을 생성 쉐이더에게 제공하는데, 생성 쉐이더는 이로부터 높이 값을 추출한다.

사각형 패치의 점을 이 높이 값만큼 수직 방향으로 올린다.

이렇게 만들어진 메시는 GPU 파이프라인의 다음 단계로 넘겨진다. 기하 쉐이더가 있다면 기하 쉐이더를 거쳐 래스터라이저에게, 기하 쉐이더가 없다면 직접 래스터라이저로 넘겨져 최종적으로 스크린에 출력된다.

💡 변위 매핑은 노멀 매핑과 근본적으로 다른 기법이다.

🌱 변위 매핑을 위한 GL 프로그램, 쉐이더, 테셀레이터

변위 매핑을 위해 GL 프로그램은 먼저 컨트롤 및 생성 쉐이더를 위한 쉐이더 오브젝트를 각각 만들어야 한다. 이를 위해서 glCreateShader를 호출하는데, 파라미터로 GL_TESS_CONTROL_SHADER와 GL_TESS_EVALUATION_SHADER를 사용한다. 또한, GL 프로그램은 패치 프리미티브를 구성하는 정점의 개수를 지정해야 한다. 다음은 변위 매핑을 위한 정점 쉐이더와 컨트롤 쉐이더의 예제 코드이다.

변위 매핑을 위한 정점 쉐이더

#version 320 es

layout(location = 0) in vec3 position;
layout(location = 1) in vec2 texCoord;

out vec3 v_position;
out vec2 v_texCoord;

void main() {
    v_position = position;  // object-space position
    v_texCoord = texCoord;
}

메인 함수는 입력받은 position과 texCoord를 그대로 복사할 뿐, gl_Position을 출력하지 않는다. 이는 정점 쉐이더 대신 생성 쉐이더가 출력할 것이다.

변위 매핑을 위한 컨트롤 쉐이더

#version 320 es

layout(vertices = 4) out;

uniform float tessLevel;

in vec3 v_position[];
in vec2 v_texCoord[];

out vec3 es_position[];
out vec2 es_texCoord[];

void main() {
    es_position[gl_InvocationID] = v_position[gl_InvocationID];
    es_texCoord[gl_InvocationID] = v_texCoord[gl_InvocationID];

    // tessellation levels
    gl_TessLevelInner[0] = tessLevel;
    gl_TessLevelInner[1] = tessLevel;
    gl_TessLevelOuter[0] = tessLevel;
    gl_TessLevelOuter[1] = tessLevel;
    gl_TessLevelOuter[2] = tessLevel;
    gl_TessLevelOuter[3] = tessLevel;
}

출력되는 정점의 개수는 컨트롤 쉐이더에 vertices라는 키워드로 지정되는데, 위 예제 코드에서 정점의 개수를 4로 지정한 것을 알 수 있다. 이는 네 개의 컨트롤 쉐이더가 공동 작업한다는 뜻이다.

또한, 컨트롤 쉐이더 간 정점 배분은 내장 변수인 gl_InvocationID를 사용해 이뤄진다. 사각형 패치 입력에 대해 총 네 개의 컨트롤 쉐이더가 공동 작업할 때, gl_InvocationID는 0부터 3까지의 값을 가진다.

컨트롤 쉐이더는 이렇게 생성 쉐이더에게 패치를 출력함과 동시에 테셀레이터에게 테셀레이션 레벨을 제공해야 한다. 이를 위해 gl_TessLevelInner와 gl_TessLevelOuter라는 내장 변수를 사용한다. Inner는 패치의 정의역 내부를 분할하고 Outer는 정의역의 경계를 분할한다. 정의역 내부는 수직, 수평 방향으로, 경계는 독립적으로 분할되며 사각형 패치를 예제로 들었기 때문에 위 코드에선 4개의 Outer 변수를 사용한다.

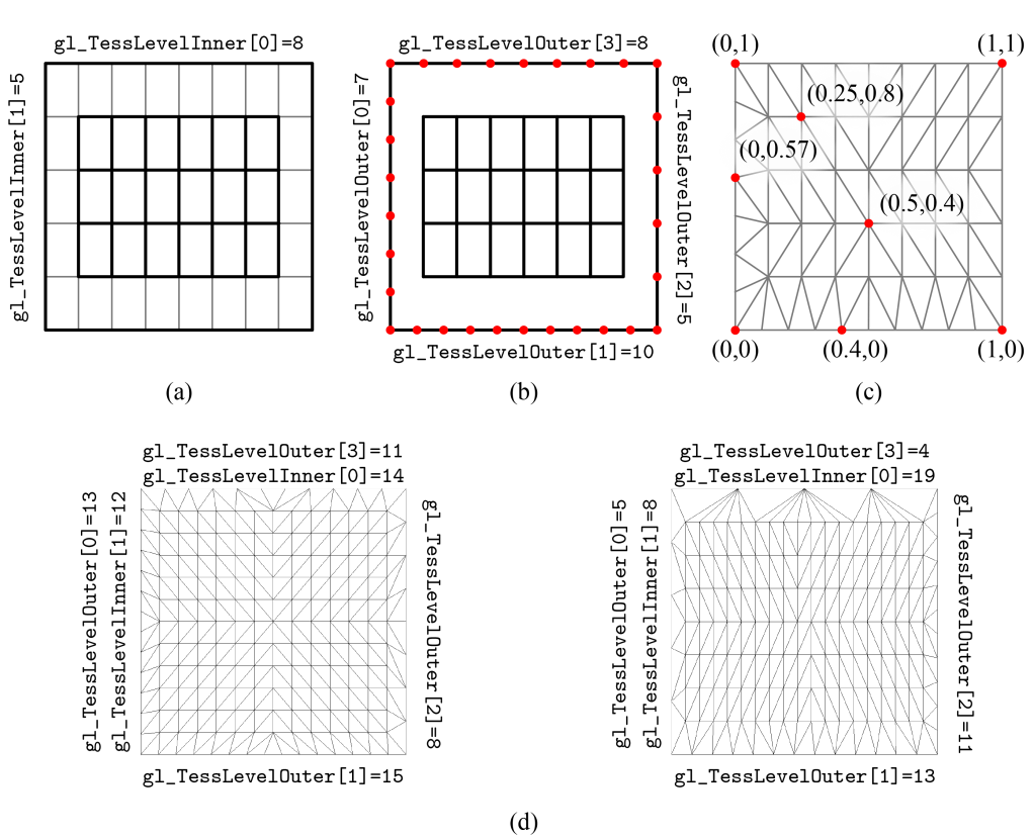
Alt Text

위 이미지의 그림-(b)에서 패치의 정의역은 수직 방향으로 8등분, 수평 방향으로 5등분되고 각 경계는 7, 10, 5, 8등분 되는 것을 확인할 수 있다. 테셀레이터는 이렇게 분할된 정의역 전체를 삼각형들로 채운다. 그림-(c)가 그 결과이다.

GL 3.2가 제공하는 테셀레이션 기능은 폴리곤 메시가 가지는 ‘근사적이며 고정적인 모델’이라는 한계를 극복할 수 있게 한다. 즉, 베지어 곡면과 같은 ‘정확한 모델’을 입력으로 받아서, 이를 원하는 만큼의 해상도를 가진 메시로 자유자재로 바꿔 사용할 수 있는 것이다. 컨트롤 쉐이더의 출력은 생성 쉐이더에게 전달될 것이다. 다음은 변위 매핑을 위한 생성 쉐이더 코드이다.

변위 매핑을 위한 생성 쉐이더

#version 320 es

laytout(quads) in;

uniform sampler2D heightMap;
uniform float dispFactor;
uniform mat4 worldMat, viewMat, projMat;

in vec3 es_position[];
in vec2 es_texCoord[];

out vec2 v_texCoord;

void main() {
    float u = gl_TessCoord.x;
    float v = gl_TessCoord.y;

    // bilinearly interpolated object-space position
    vec3 lowerPos = mix(es_position[0], es_position[1], u);
    vec3 upperPos = mix(es_position[2], es_position[3], u);
    vec3 position = mix(lowerPos, upperPos, v);

    // bilinearly interpolated texture coordinates
    vec2 lowerTex = mix(es_texCoord[0], ex_texCoord[1], u);
    vec2 upperTex = mix(es_texCoord[2], ex_texCoord[3], u);
    v_texCoord = mix(lowerTex, upperTex, v);

    // vertical displacement
    float height = texture(heightMap, v_texCoord).z;
    position += dispFactor * vec3(0.0, 0.0, height);

    // clip-space position
    gl_Position = projMat * viewMat * worldMat * vec4(position, 1.0);
}

quads는 사각형 패치를 입력으로 받는다는 것을 의미한다. 테셀레이터가 만든 2차원 삼각형 메시의 각 정점마다 하나의 생성 쉐이더가 작동되는데, 정점의 (u, v) 좌표는 gl_TessCoord라는 내장 변수에 저장되어 생성 쉐이더에게 전달된다. 메인 함수에서 이를 이용해 (u, v)를 추출한다.

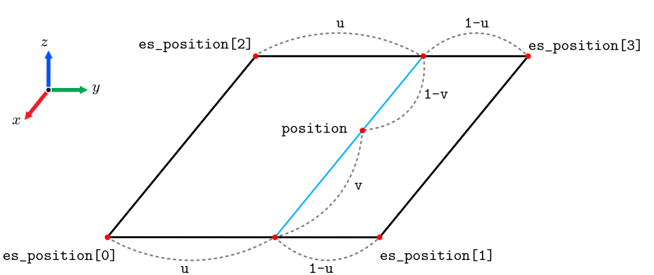
Alt Text

생성 쉐이더는 es_position[]을 겹선형 패치의 컨트롤 포인트로 취급하는데, gl_TessCoord에서 추출한 (u, v)를 사용해 겹선형 패치 위의 한 점을 생성한다. 위 이미지는 es_position[]을 겹선형 보간하여 한 점(position)을 생성하는 과정을 보여준다.

💡 겹선형 보간 과정에서 사용된 mix(A, B, u) 내장 함수는 (1 - u)A + uB를 리턴한다.

마지막으로 내장 함수 texture를 이용하여 하이트맵에서 높이 값을 추출해 position의 z값에 적용하면 해당 좌표는 height만큼 수직 방향으로 옮겨질 것이다.

이렇게 변위(Displacement)가 완료된 정점은 클립 공간으로 변환되어 출력된다. 마지막 줄을 보면 정점 쉐이더가 담당했던 gl_Position 출력을 이제 생성 쉐이더가 수행하는 것을 알 수 있다.

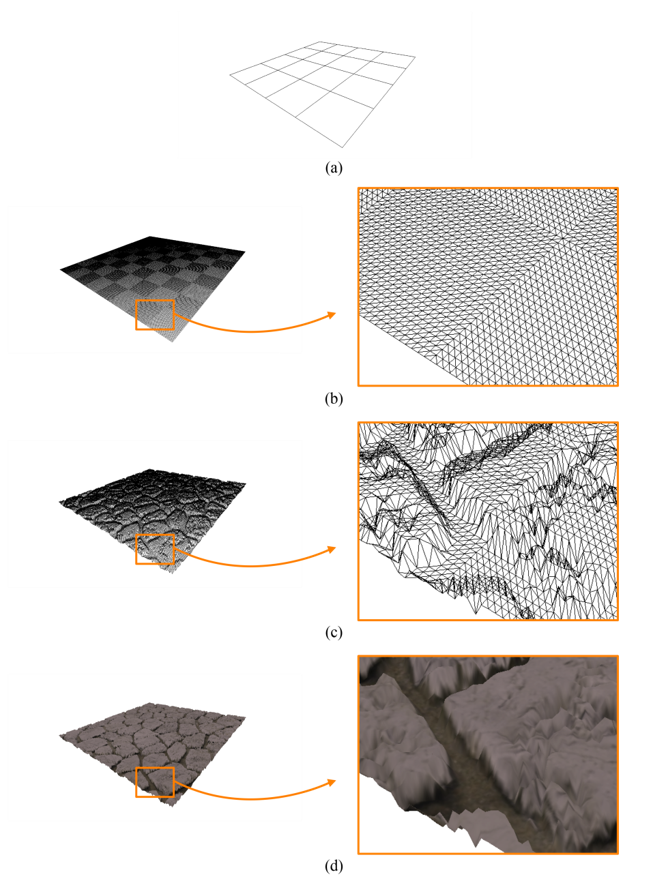
Alt Text

위 이미지는 앞서 보았던 쉐이더들을 사용해 넓은 면적의 보도를 처리한 결과를 보여준다. 보도 표면은 사각형 메시(Quad Mesh)로 정의되었고, 이를 위한 인덱스 배열은 사각형 당 네 개, 총 64개의 원소를 가진다. 폴리곤 메시를 렌더링하려면 드로우 콜을 해야한다. 삼각형 메시를 렌더링 할 때 함수 glDrawElements를 호출하고 첫 번째 파라미터로 GL_TRIANGLES를 입력했었지만, 사각형 메시는 GL_PATCHES를 사용한다.

glDrawElements(GL_PATCHES, 64, GL_UNSIGNED_SHORT, 0)

👻 PN-삼각형

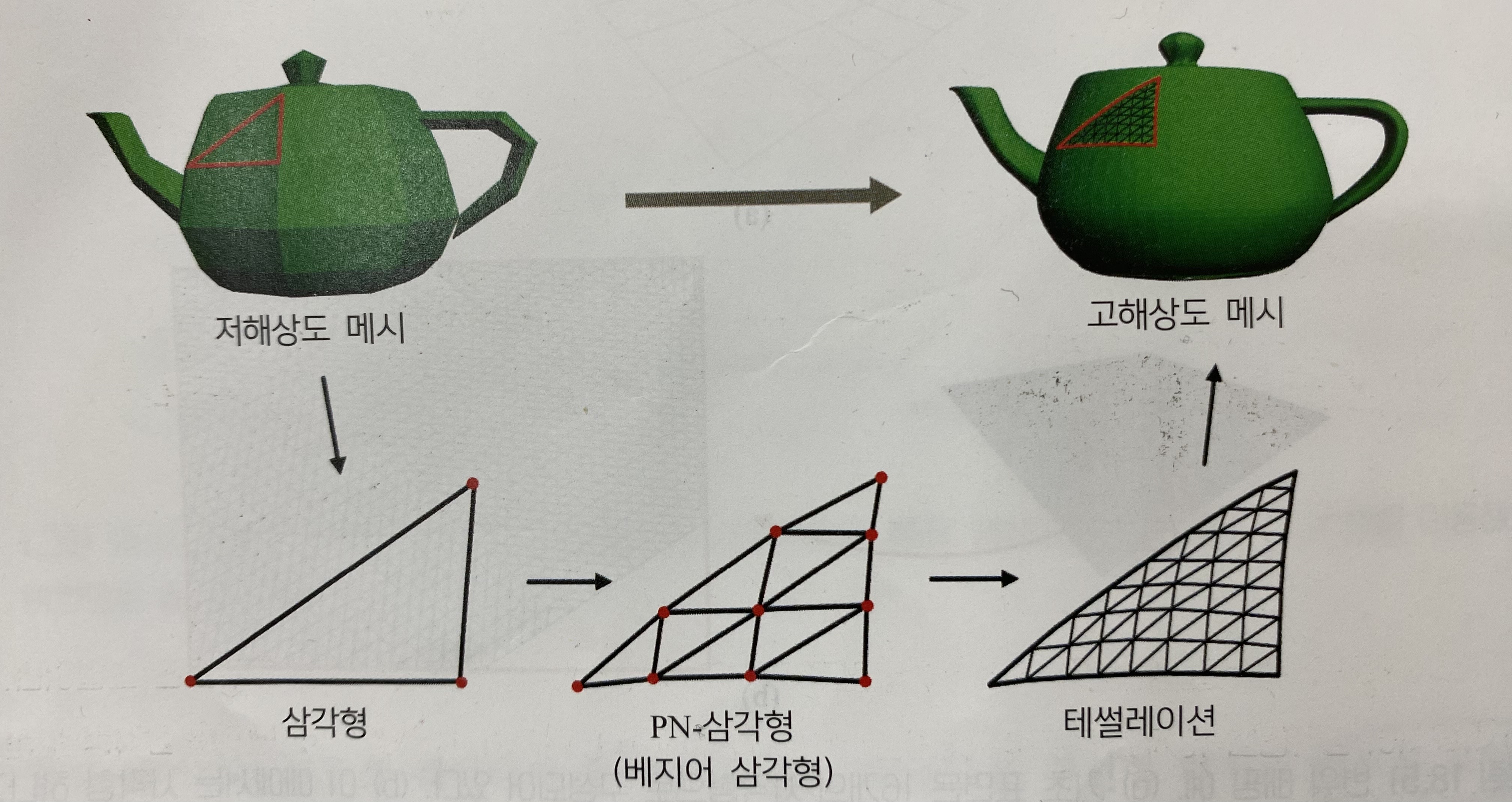
Alt Text

PN-삼각형은 메시의 한 삼각형으로부터 유도한 베지어 삼각형이라고 정의할 수 있다. 하나의 PN-삼각형은 테셀레이션 과정을 거쳐 다수의 작은 삼각형들을 만들고 이들은 원래의 삼각형을 대체한다. 저해상도 삼각형 메시를 구성하는 모든 삼각형을 이런 방식으로 처리하면 부드러운 고해상도 메시를 얻을 수 있다.

💡 여기서 P는 Point를, N은 Normal을 의미한다.

🌱 컨트롤 포인트 계산

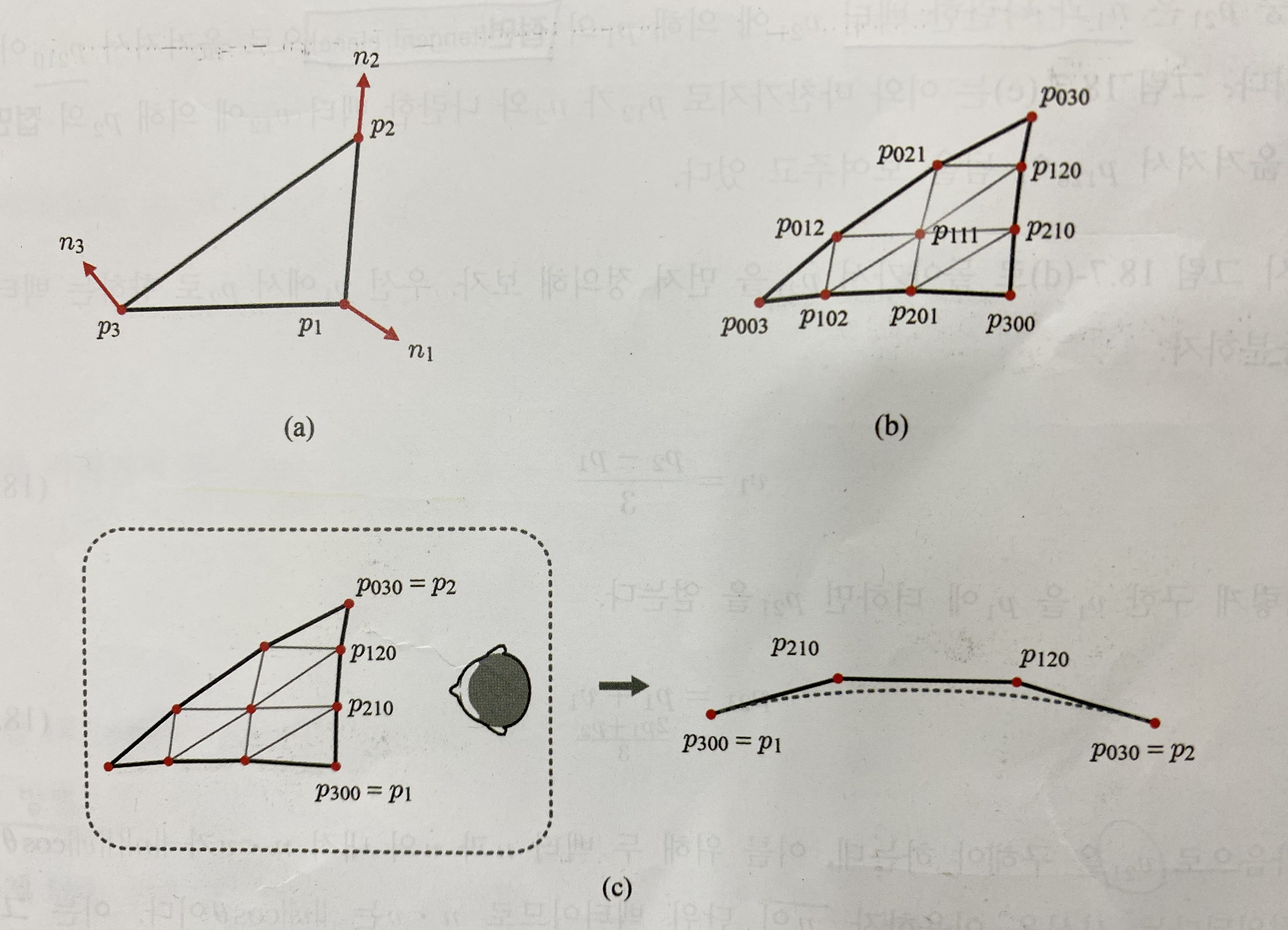
Alt Text

위 이미지의 그림-(a)는 입력으로 주어진 삼각형 메시에서 추출한 삼각형이다. 각 정점은 위치와 노멀 정보를 가지고 있으며, 이 삼각형을 3차 베지어 삼각형으로 바꾸기 위해 그림-(b)에 보이는 것처럼 컨트롤 포인트를 결정해야 한다.

각 모퉁이에 위치한 컨트롤 포인트는 정점의 위치를 나타내는 p_i로 설정된다. 테두리에 위치한 컨트롤 포인트들은 해당 변의 양 끝 정점 애트리뷰트를 이용하여 결정되며 이 변은 3차 베지어 곡선이 된다.

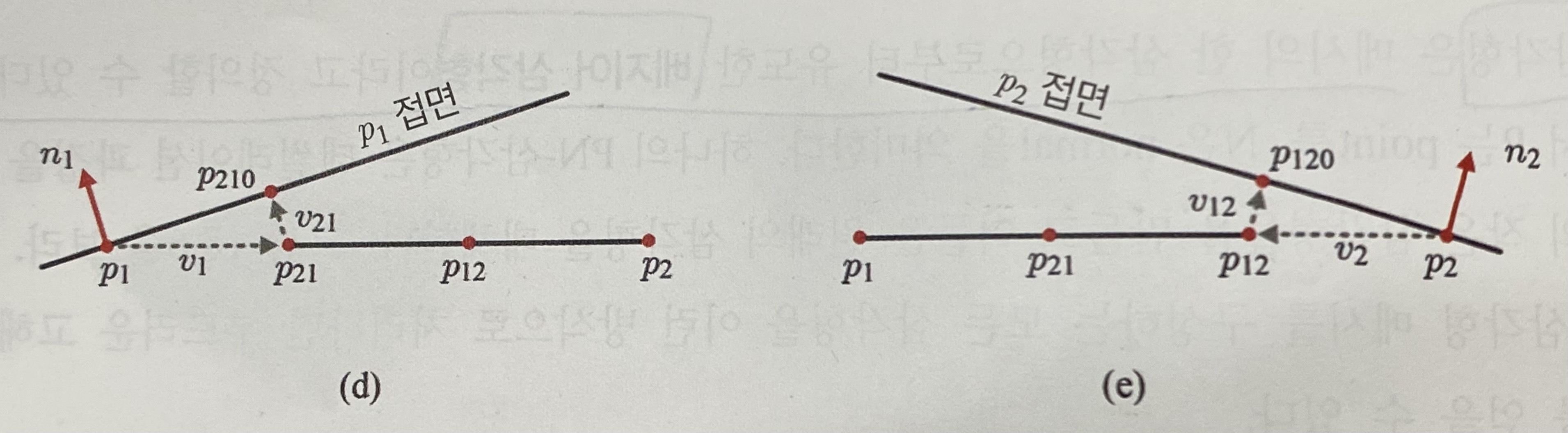
그림-(d)는 p₁과 p₂를 잇는 변을 3등분해서 컨트롤 포인트 p₂₁과 p₁₂를 만드는 과정을 보여준다. p₂₁의 경우 n₁과 나란한 벡터 v₂₁에 의해 p₁의 접면(Tangent Plane)으로 옮겨져서 p₂₁₀이 될 것이다. 그림-(e)는 p₁₂의 경우이며, 접면에 옮겨져 p₁₂₀이 됨을 보여주고 있다.

위 과정을 식으로 정리하면 p₂₁은 다음과 같이 정의된다.

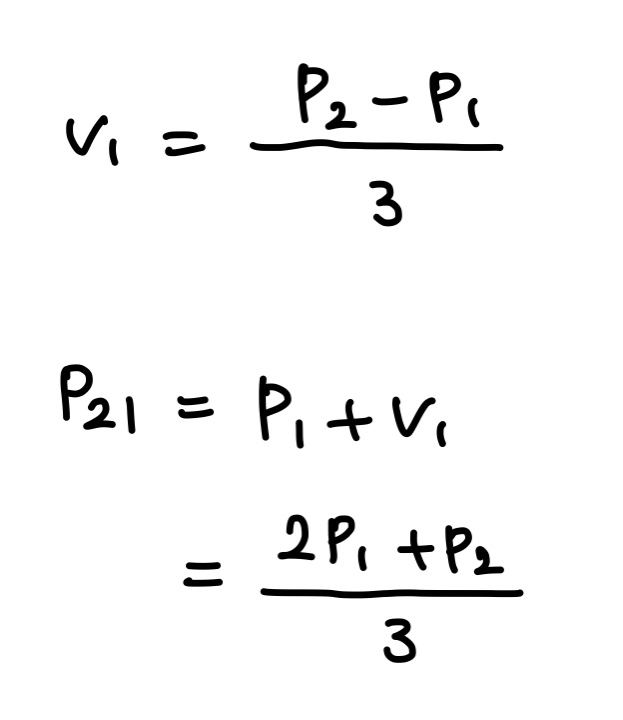
p₁에서 p₂로 향하는 벡터를 3등분하여 v₁을 구하고 여기에 p₁을 더하여 p₂₁을 정의할 수 있다.

다음으로 v₂₁을 구해야 하는데, 이를 위해 두 벡터 n과 v의 내적을 이용한다.

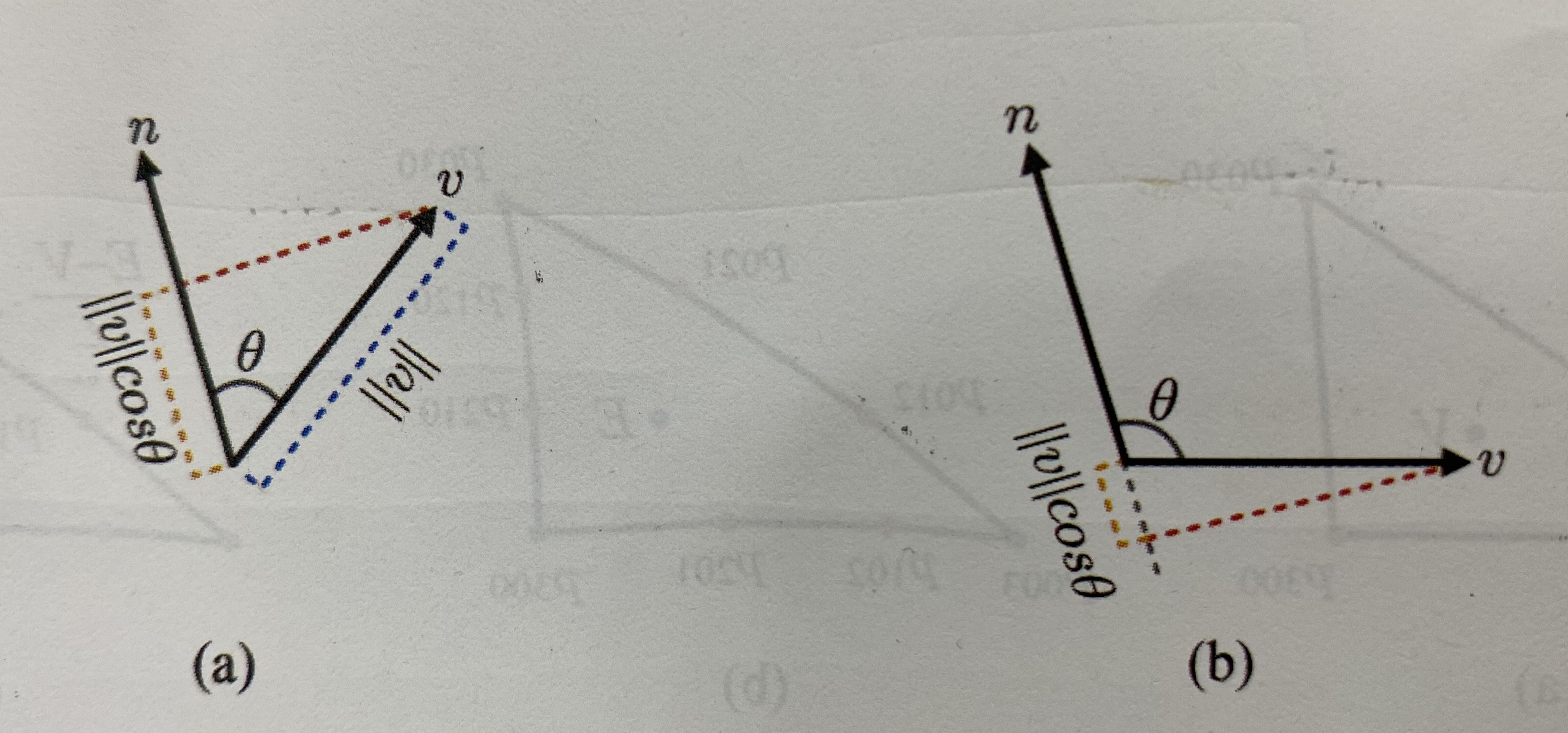
Alt Text

n·v = ||n||||v||cosθ에서 n은 단위 벡터이므로 결과적으로 ||v||cosθ임을 알 수 있다. 이 말인 즉슨, n과 v의 내적은 n에 투영된 v의 길이를 의미한다.

n₁에 투영된 v₁의 길이를 구하면 아래와 같다.

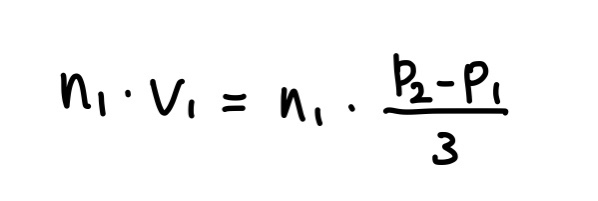
그런데, 두 벡터는 둔각을 이루므로 결과값은 음수가 될 것이다. 이를 양수로 바꾸고 여기에 n₁을 곱하면 벡터 v₂₁을 얻을 수 있다.

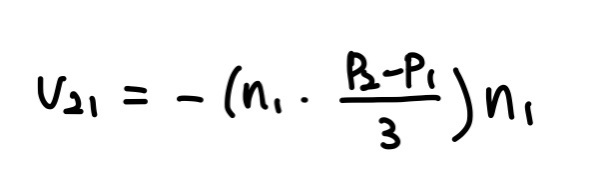
마지막으로, 시작점 p₂₁에 v₂₁을 더하면 p₂₁₀을 얻는다.

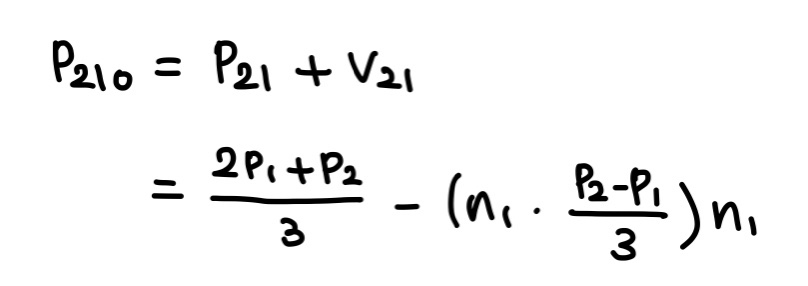
이와 마찬가지 방식으로 p₁₂₀을 계산할 수 있다.

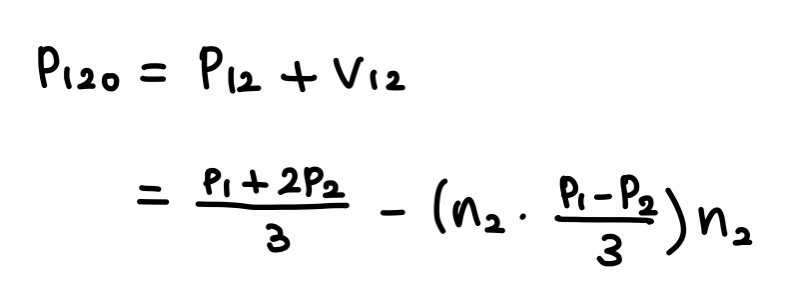
나머지 테두리에 위치한 컨트롤 포인트 p₀₂₁, p₀₁₂, p₁₀₂, p₂₀₁ 역시 비슷한 방법으로 계산된다.

이제 남은 것은 내부의 컨트롤 포인트 p₁₁₁이다. 이는 이제까지 계산한 9개의 컨트롤 포인트를 이용하여 결정된다.

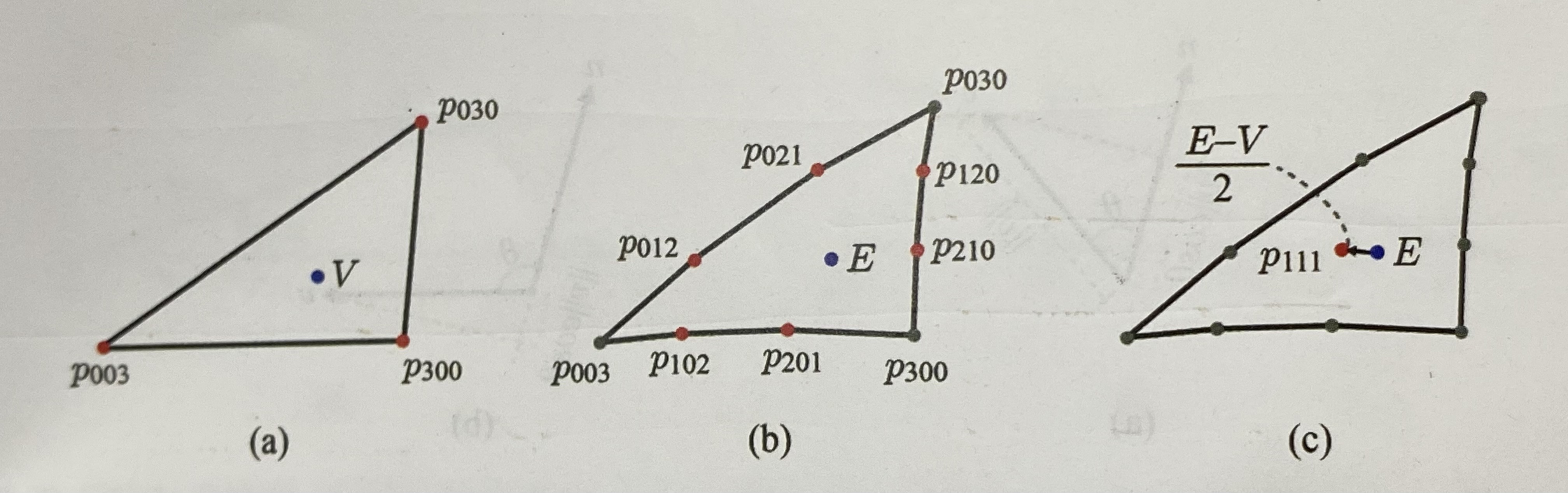
Alt Text

우선, 모퉁이 컨트롤 포인트의 평균(V)과 6개의 테두리 컨트롤 포인트의 평균(E)을 구하면 다음과 같다.

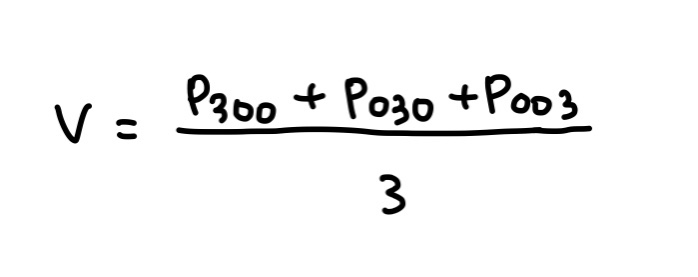
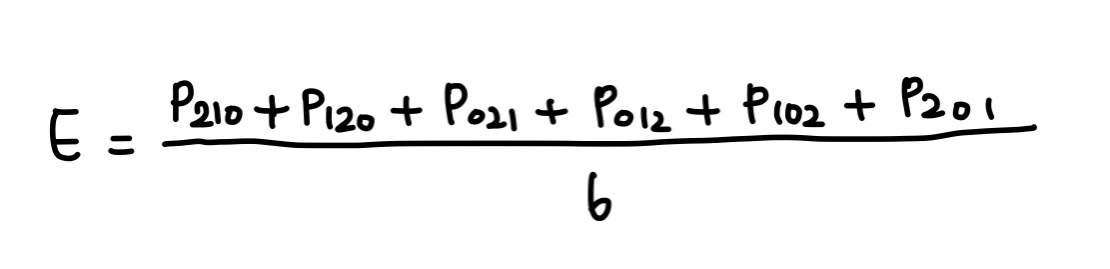
마지막으로, E를 (E - V)/2만큼 옮겨서 p₁₁₁을 결정한다.

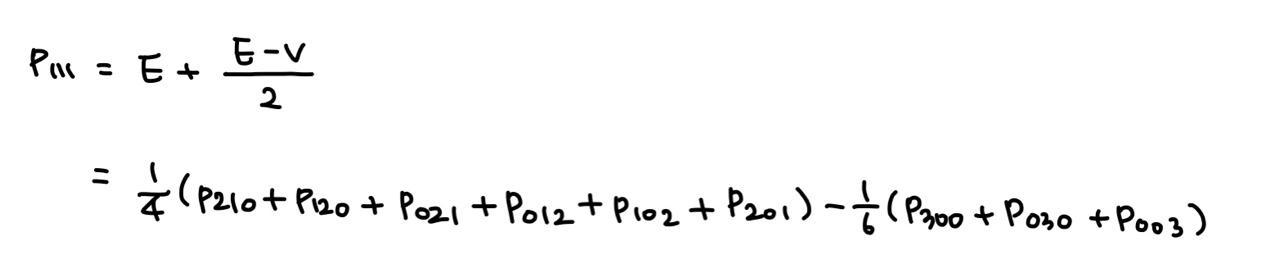
Alt Text

💡 이 밖에도 여러가지 다른 방법이 있는 것 같은데, 해당 교재에서는 이 방식을 사용하는 듯 하다.

이렇게 하여 10개의 컨트롤 포인트를 모두 결정했다. 이 결과로 아래의 그림-(a)에서 보여지는 것처럼 3차 베지어 삼각형의 식 p(u, v, w)를 얻게 되는데, 그러면 균일하게 샘플한 (u, v, w) 좌표들을 이용하여 베지어 삼각형을 테셀레이션할 수 있다. 즉, 각각의 (u, v, w)를 p(u, v, w)에 대입하여 3차원 정점 (x, y, z)를 얻는데, 이들 정점을 연결하여 고해상도 삼각형 메시를 구성할 수 있게 되는 것이다.

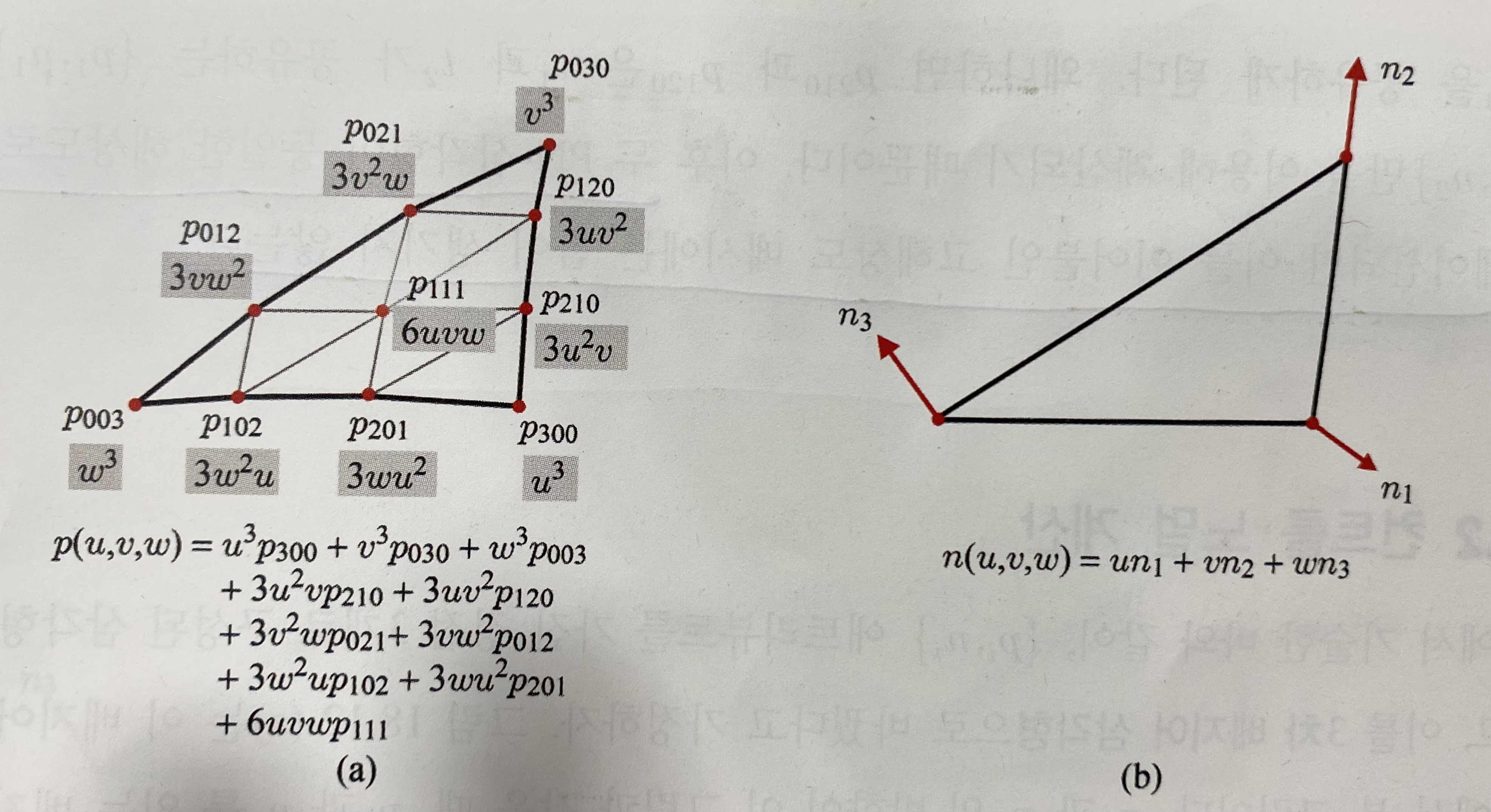
Alt Text

메시를 렌더링하기 위해서는 이러한 정점 위치만으로는 부족하며 정점 노멀이 추가로 필요하다. 정점 노멀을 계산하는 가장 간단한 방법은 입력으로 주어진 세 모퉁이 노멀의 무게중심 조합(Barycentric Combination)을 택하는 것이다. 이 무게중심 조합을 n(u, v, w)라 표기할 때, 이는 결국 {n₁, n₂, n₃}에 기반한 1차 베지어 삼각형이라고 볼 수 있다. 컨트롤 포인트와 대비되도록 이를 컨트롤 노멀이라 부른다.

이렇게 정점의 위치뿐만 아니라 정점 노멀까지 구하면 메시를 렌더링할 수 있는 모든 준비가 되었다. 하지만 n(u, v, w)는 1차식이므로 문제를 야기할 수 있기 때문에, 이에 대해 알아보고 2차 베지어 삼각형으로 정의된 n(u, v, w)에 대해 알아보자.

🌱 컨트롤 노멀 계산

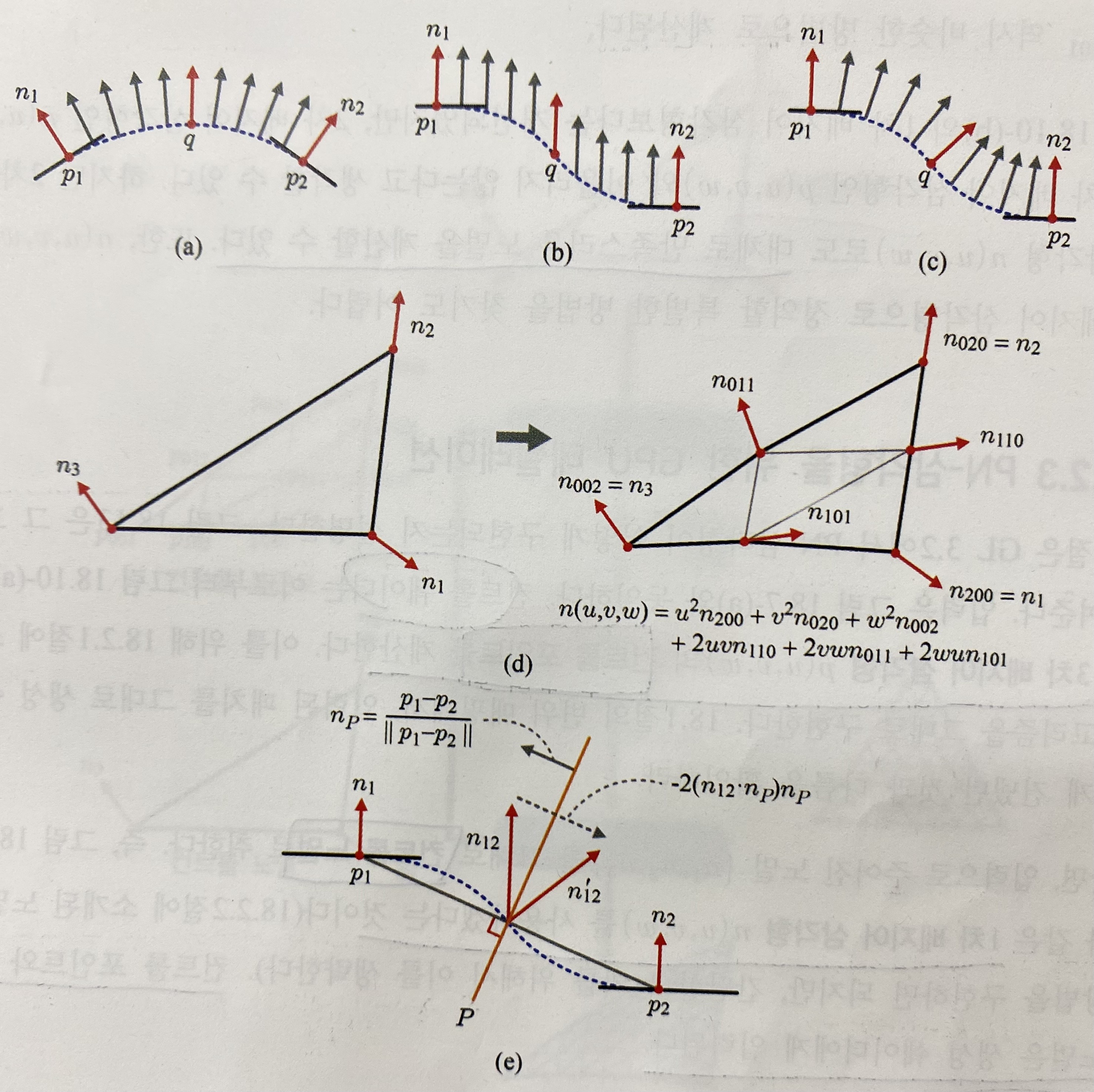
Alt Text

위 이미지의 그림-(a)의 경우 앞에서 구한 방식으로 노멀을 구한 결과이다. 이는 점선으로 표현된 곡면과 수직을 이루므로 적절한 선택으로 보이지만 그림-(b)와 같은 물체의 경우를 생각해보면 반드시 정확한 결과를 도출하는 게 아님을 알 수 있다. 적절한 결과는 그림-(c)가 되어야 할 것이다. 이는 n(u, v, w)를 2차 베지어 삼각형으로 정의한 결과이다.

이를 위한 여러 가지 방법이 있을텐데, 그림-(e)는 휴리스틱 한 가지를 보여준다. p₁과 p₂를 잇는 선분에 수직인 평면 P를 생각해 보자. P의 노멀 n_P는 다음과 같이 계산된다.

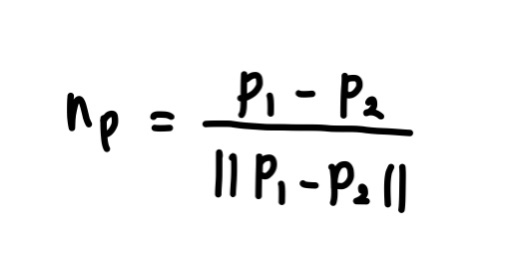
정점 노멀 n₁과 n₂를 더한 결과를 n₁₂라 할 때, n₁₂와 n_P의 내적은 n₁₂를 n_P에 투영한 길이가 된다. 이를 -2n_P와 곱한 후 n₁₂에 더한 것을 n’₁₂라 하자. 이는 n₁₂를 P에 대해 반사시킨 것이다.

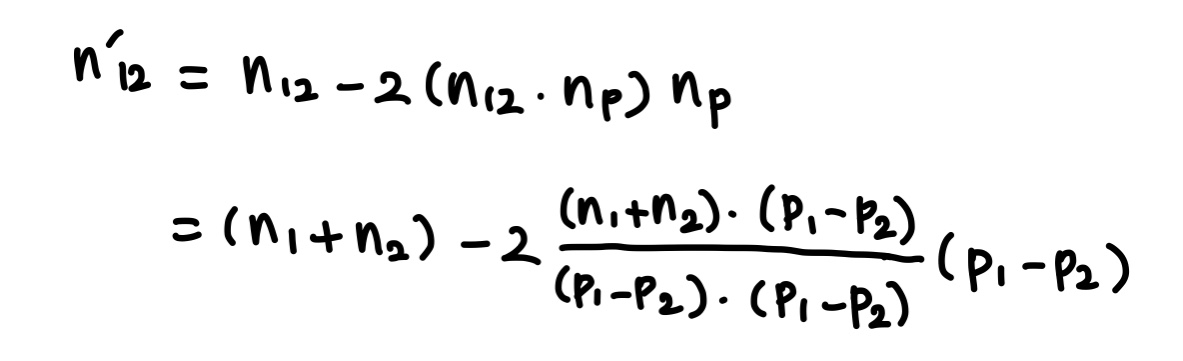
Alt Text

이렇게 계산된 n’₁₂를 정규화하면 컨트롤 노멀 n₁₁₀을 얻을 수 있다. 다른 컨트롤 노멀역시 비슷한 방법으로 계산된다.

2차 베지어 삼각형은 1차 베지어 삼각형보다는 개선되었지만 3차 베지어 삼각형인 p(u, v, w)와 어울리지 않는다고 생각할 수 있다. 하지만 2차 베지어 삼각형 n(u, v, w)로도 대체로 만족스러운 노멀을 계산할 수 있다. 또한, n(u, v, w)를 3차 베지어 삼각형으로 정의할 특별한 방법을 찾기도 어렵다.

🌱 PN-삼각형을 위한 GPU 테셀레이션

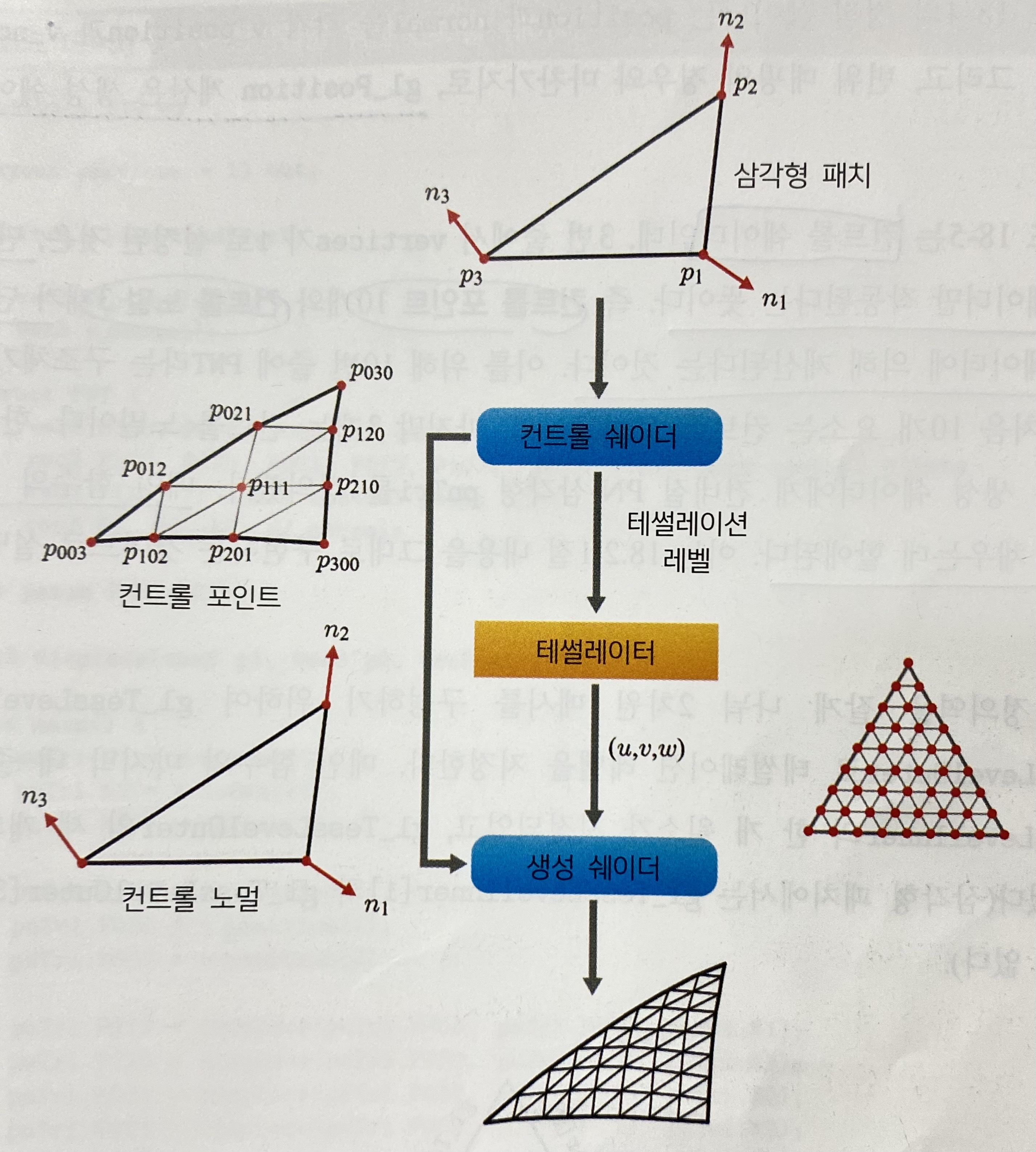
Alt Text

입력은 정점 위치와 노멀 정보가 담긴 1차 베지어 삼각형으로 정의된 삼각형 패치를 받으며 컨트롤 쉐이더는 이로부터 3차 베지어 삼각형 p(u, v, w)의 컨트롤 포인트를 계산한다. 반면, 입력으로 주어진 노멀은 그대로 컨트롤 노멀로 취하게 된다. 즉, 1차 베지어 삼각형 n(u, v, w)를 사용하겠다는 것이다. 이렇게 만들어진 컨트롤 포인트와 컨트롤 노멀은 생성 쉐이더에게 입력된다.

컨트롤 쉐이더는 테셀레이션 레벨을 결정해서 테셀레이터에게 알려준다. 테셀레이터는 컨트롤 쉐이더가 지정해주는 대로 삼각형 정의역(Domain)을 잘게 나눠 2차원 메시를 구성하며, 이러한 메시의 정점마다 무게중심 좌표 (u, v, w)가 할당된다.

이렇게 만들어진 2차원 메시의 각 정점에 대해 생성 쉐이더가 한 번 실행된다. 컨트롤 쉐이더가 건네준 컨트롤 포인트와 컨트롤 노멀을 사용해 각각 p(u, v, w)와 n(u, v, w)를 만든 후, 테셀레이터가 건네준 (u, v, w)를 각각의 식에 대입하여 3차원 정점의 위치와 노멀을 계산한다. 이런 방식으로 2차원 메시가 모두 처리되면 부드러운 고해상도 메시가 생성되고 이는 GPU 파이프라인의 다음 단계로 넘겨진다.

🌱 PN-삼각형을 위한 GL 프로그램, 쉐이더, 테셀레이터

PN-삼각형을 위한 정점 쉐이더, 컨트롤 쉐이더, 생성 쉐이더의 예제 코드를 가볍게 살펴보고 각 과정에서 어떠한 처리가 이루어지는지 알아보자.

PN-삼각형을 위한 정점 쉐이더

#version 320 es

layout(location = 0) in vec3 position;
layout(location = 1) in vec3 normal;

out vec3 v_position;
out vec3 v_normal;

void main() {
    v_position = position;  // object-space position
    v_normal = normal;
}

변위 매핑과 마찬가지로 입력으로 받은 정점 위치와 노멀을 그대로 복사한다. 변위 매핑과 한 가지 차이가 있다면 텍스처 좌표 대신 노멀을 입력으로 받아 사용하게 되는 것이다. 또한 마찬가지로 gl_Position 계산은 생성 쉐이더에게 맡긴다.

PN-삼각형을 위한 컨트롤 쉐이더

#version 320 es

layout(vertices = 1) out;

uniform float tessLevel;

in vec3 v_position[];
in vec3 v_normal[];

struct PNT {
    vec3 P300, P030, P003;  // corner control points
    vec3 P210, P120, P021, P012, P102, P201;    // mid-edge control points
    vec3 P111;  // inner control point
    vec3 N1, N2, N3;
};
out patch PNT pnTri;

vec3 displace(vec3 p1, vec3 p2, vec3 n1);

void main() {
    pnTri.N1 = v_normal[0];
    pnTri.N2 = v_normal[1];
    pnTri.N3 = v_normal[2];

    pnTri.P300 = v_position[0];
    pnTri.P030 = v_position[1];
    pnTri.P003 = v_position[2];

    pnTri.P210 = displace(pnTri.P300, pnTri.P030, pnTri.N1);
    pnTri.P120 = displace(pnTri.P030, pnTri.P300, pnTri.N2);
    pnTri.P021 = displace(pnTri.P030, pnTri.P003, pnTri.N2);
    pnTri.P012 = displace(pnTri.P003, pnTri.P030, pnTri.N3);
    pnTri.P102 = displace(pnTri.P003, pnTri.P300, pnTri.N3);
    pnTri.P201 = displace(pnTri.P300, pnTri.P003, pnTri.N1);

    vec3 V = (pnTri.P300 + pnTri.P030 + pnTri.P003) / 3.0;
    vec3 E = (pnTri.P210 + pnTri.P120 + pnTri.P021 + pnTri.P012 + pnTri.P102 + pnTri.P201) / 6.0;
    pnTri.P111 = E + (E - V) / 2.0;

    gl_TessLevelOuter[0] = tessLevel;
    gl_TessLevelOuter[1] = tessLevel;
    gl_TessLevelOuter[2] = tessLevel;
    gl_TessLevelInner[0] = tessLevel;
}

vec3 displace(vec3 p1, vec3 p2, vec3 n1) {
    return (2.0 * p1 + p2) / 3.0 - dot(n1, (p2 - p1) / 3.0) * n1;
}

위 예제 코드는 컨트롤 포인트 10개와 컨트롤 노멀 3개가 단 하나의 컨트롤 쉐이더에 의해 계산된다는 것을 의미한다. 이를 위해 구조체 PNT가 정의되었는데 첫 10개 요소는 컨트롤 포인트이고 마지막 3개는 컨트롤 노멀이다.

pnTri는 생성 쉐이더에게 건네질 PN-삼각형을 의미하며 메인 함수에서 pnTri를 채우게 된다.

마찬가지로 삼각형 정의역을 나누기 위해 gl_TessLevelInner와 gl_TessLevelOuter를 사용하여 테셀레이션 레벨을 지정한다. 삼각형 패치를 위한 테셀레이션 레벨은 다음과 같이 정의된다.

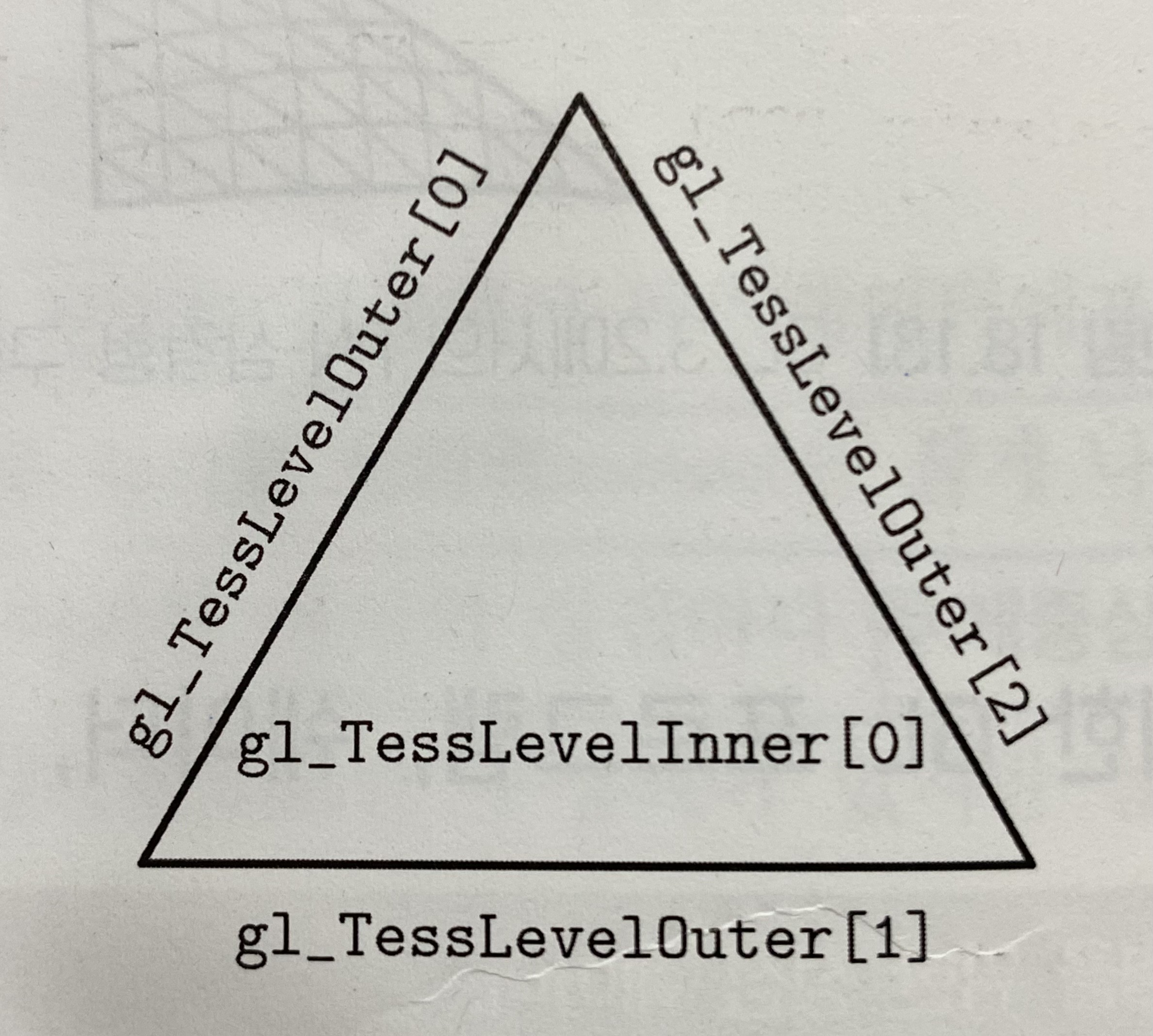
Alt Text

삼각형 내부 분할 과정을 자세하게 살펴보기 위해 gl_TessLevelInner[0]를 간단히 ‘inner TL’이라 표기할 것이다.

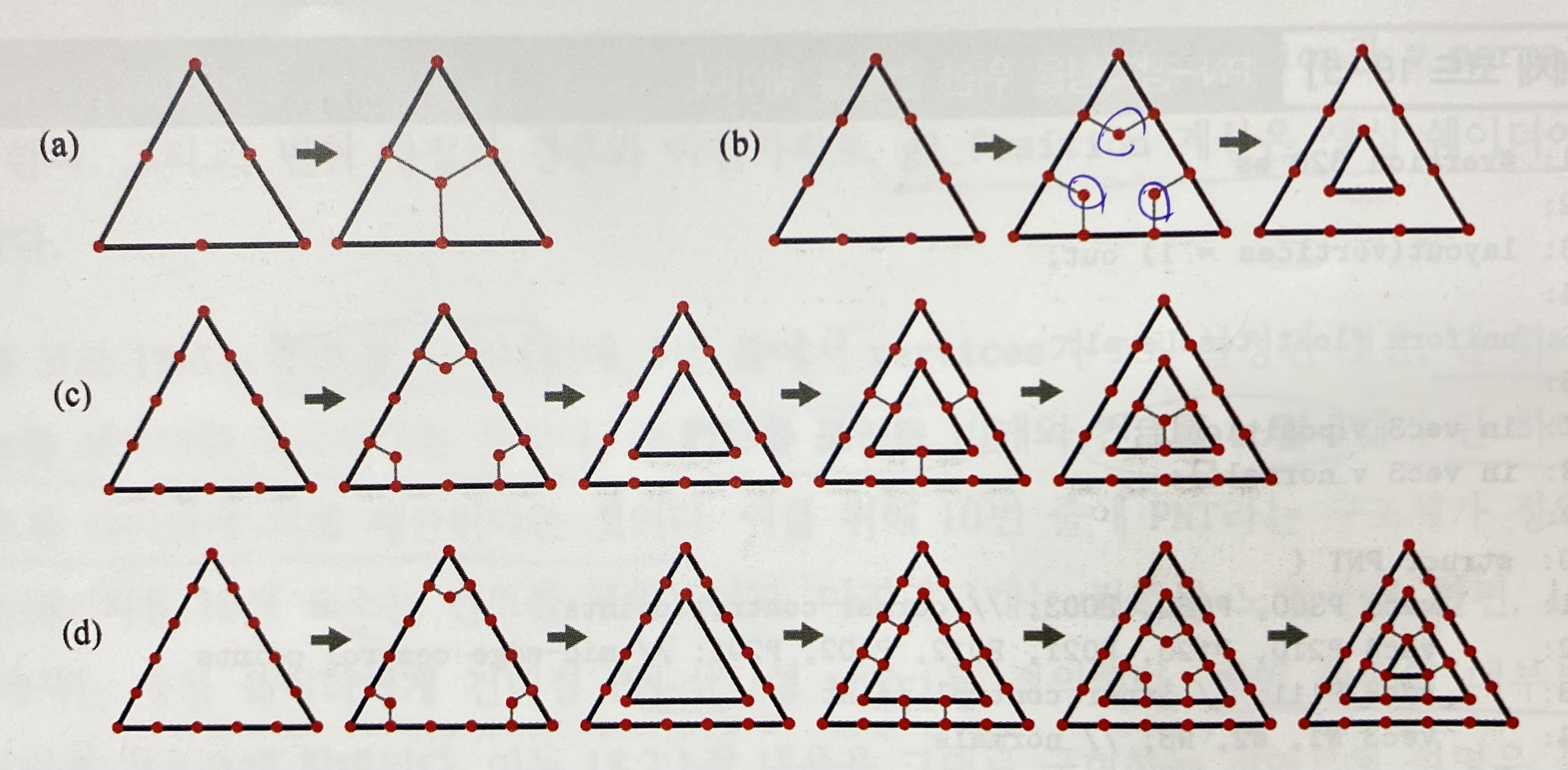
Alt Text

우선 inner TL이 2로 지정되었다고 가정할 때, 위 이미지의 그림-(a)처럼 삼각형 정의역의 세 변은 모두 2등분되며 각 변의 등분점을 가로지르는 직선은 삼각형의 중심에서 만날 것이다. inner TL이 3으로 지정되었다면, 그림-(b)처럼 삼각형 정의역의 모든 변은 3등분되며 삼각형 한 정점에 인접한 등분점 두 개를 가로지르는 직선 둘은 한 점에서 만나게 된다. 삼각형 내부에 그러한 점은 총 세 개가 있으며 이들은 하나의 작은 삼각형을 만든다. 이 삼각형은 원래 주어진 삼각형과 중심을 공유한다.

그림-(c)는 inner TL이 4로 지정되었을 경우를 보여주는데, 마찬가지로 세 변은 4등분되고 이전에서 보았던 과정을 반복 수행하며 삼각형 정의역을 잘게 나누게 된다. 그림-(d)는 inner TL이 5로 지정되었을 경우를 보여준다.

이렇게 내부 분할이 완료되면 gl_TessLevelOuter로 인해 삼각형 정의역의 경계를 분할하게 된다. 다음은 정의역 분할의 한 예시와 결과를 보여준다.

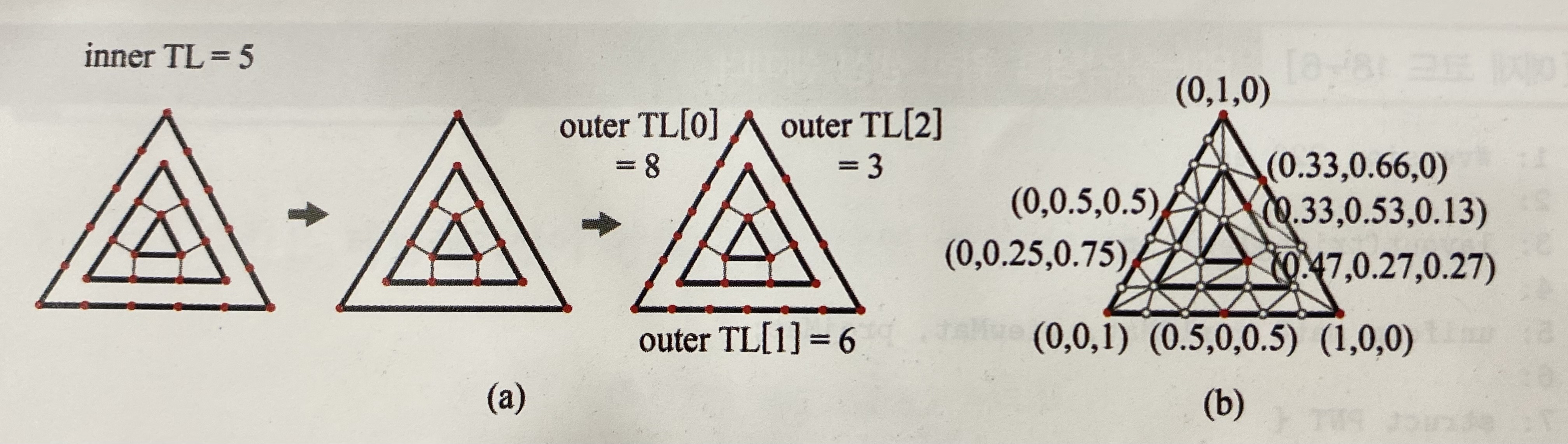
Alt Text

물론 ‘outer TL’은 gl_TessLevelOuter를 의미한다.

테셀레이터는 이렇게 분할된 정의역을 삼각형들로 채우게 되며 2차원 삼각형 메시의 각 정점에는 무게중심 좌표 (u, v, w)가 할당된다.

PN-삼각형을 위한 생성 쉐이더

#version 320 es

layout (triangles) in;

uniform mat4 worldMat, viewMat, projMat;

struct PNT {
    vec3 P300, P030, P003;  // corner control points
    vec3 P210, P120, P021, P012, P102, P201;    // mid-edge control points
    vec3 P111;  // inner control point
    vec3 N1, N2, N3;
};
in patch PNT pnTri;

out vec3 v_normal;

void main() {
    // powers of the parameters
    float u1 = gl_TessCoord.x, v1 = gl_TessCoord.y, w1 = gl_TessCoord.z;
    float u2 = pow(u1, 2.0), v2 = pow(v1, 2.0), w2 = pow(w1, 2.0);
    float u3 = pow(u1, 3.0), v3 = pow(v1, 3.0), w3 = pow(w1, 3.0);

    // position evaluation
    vec3 position = vec3(0.0);
    position += pnTri.P300 * u3 + pnTri.P030 * v3 + pnTri.P003 * w3;
    position += pnTri.P210 * 3.0 * u2 * v1 + pnTri.P120 * 3.0 * u1 * v2;
    position += pnTri.P021 * 3.0 * v2 * w1 + pnTri.P012 * 3.0 * v1 * w2;
    position += pnTri.P102 * 3.0 * w2 * u1 + pnTri.P201 * 3.0 * w1 * u2;
    position += pnTri.P111 * 6.0 * u1 * v1 * w1;

    // clip-space position
    gl_Position = projMat * viewMat * worldMat * vec4(position, 1./0);

    // normal evaluation
    vec3 normal = pnTri.N1 * u1 + pnTri.N2 * v1 + pnTri.N3 * w1;

    // world-space normal
    v_normal = normalize(transpose(inverse(mat3(worldMat))) * normal);
}

3번째 줄의 triangles는 삼각형 패치가 입력되었음을 의미한다. 컨트롤 쉐이더가 건네준 PN-삼각형은 in patch PNT pnTri;로 정의되었다.

테셀레이터가 만든 2차원 삼각형 메시의 각 정점마다 하나의 생성 쉐이더가 작동되는데, 이로부터 3차원 정점의 위치와 노멀을 계산하기 위해 생성 쉐이더는 pnTri와 gl_TessCoord를 사용한다.

💡 gl_TessCoord는 무게중심 좌표 (u, v, w)를 저장하고 있는 3차원 벡터이다. 사각형 패치를 처리하는 경우 첫 두 원소가 (u, v)를, 세 번째 원소는 0을 가진다.

이후에 정점 위치는 각 정점의 가중치를 이용하여 만들어진 3차 베지어 삼각형 p(u, v, w)를 의미하며 컨트롤 노멀은 무게중심 조합을 구하게 된다. 최종적으로 구해진 노멀을 월드 공간의 노멀로 변경된 후 GPU 파이프라인의 다음 단계로 넘겨진다.

저해상도 폴리곤 메시가 GPU 파이프라인에 입력되었다고 가정하자. 이는 우선 정점 쉐이더에 의해 처리되는데, 정점 쉐이더는 다양한 애니메이션 혹은 물리 시뮬레이션을 메시의 각 정점에 적용할 것이다. 그런데 애니메이션과 물리 시뮬레이션은 많은 시간을 소요하는 복잡한 알고리즘을 구현한 경우가 많다. 따라서 이를 저해상도 메시에 적용하는 것은 효율적인 선택이다. 이렇게 애니메이션 혹은 물리 시뮬레이션을 거친 물체를 테셀레이션을 통해 부드러운 고해상도 메시로 바꾸면 렌더링 품질이 높아질 것이다.

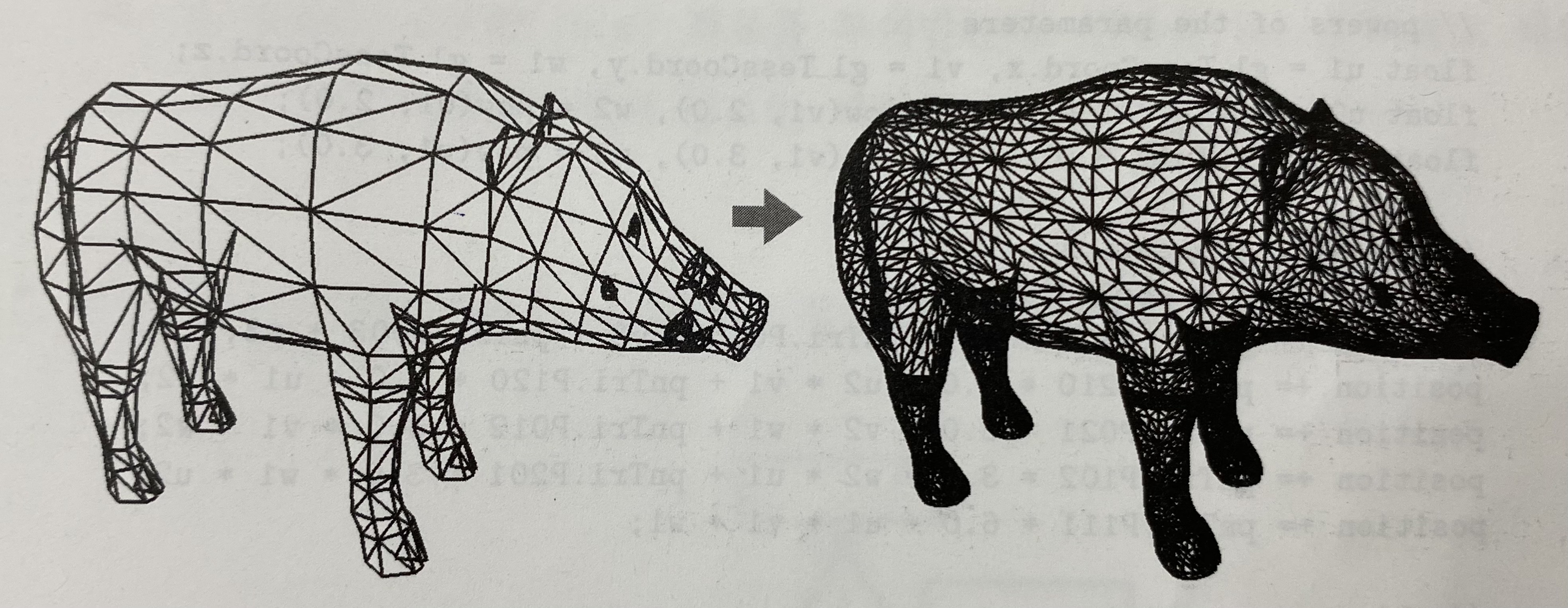
💡 PN-삼각형 적용 예

👻 글을 마치며

이번 시간에는 테셀레이션에 대해 알아보았다. 단어는 많이 들었었는데 정확히 어떠한 과정을 정의하는지 자세히 알지 못했는데 이번 시간에 완벽하게 학습할 수 있었던 것 같다. 다만 메시를 직접적으로 변경하여 고해상도로 바꾸는 작업이 어떻게 렌더링 품질을 높이는지 그 과정에 대해서는 조금 더 깊게 공부해야 할 것 같다. 항상 순서가 헷갈리는데 이 부분은 확실히 잡고 넘어가야할 것 같다😭 그래도 이 챕터를 마지막으로 스터디 계획 상 진도는 모두 끝이 났다!ヾ(•ω•`)o 고생했따 나 자신!

관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음

[Computer Graphics] #18. GPU 테셀레이션

👻 GPU 테셀레이션

👻 변위 매핑

🌱 변위 매핑을 위한 GPU 테셀레이션

🌱 변위 매핑을 위한 GL 프로그램, 쉐이더, 테셀레이터

👻 PN-삼각형

🌱 컨트롤 포인트 계산

🌱 컨트롤 노멀 계산

🌱 PN-삼각형을 위한 GPU 테셀레이션

🌱 PN-삼각형을 위한 GL 프로그램, 쉐이더, 테셀레이터

👻 글을 마치며

Leave a comment

You may also enjoy

[Copy LostArk] #0. 로아 모작으로 포폴 준비 시작!

[Operating System] #6주차 - Storage Management

[Operating System] #5주차 - 퀴즈 풀이

[Operating System] #5주차 - Virtual Memory