[Computer Graphics] #4-1. 좌표계와 변환 연습문제 풀이
👻 연습문제 풀이
4장 좌표계와 변환 챕터의 연습문제는 총 6개이다.
🌱 1
- 문제
행렬과 벡터를 곱하는데 열벡터 대신 행벡터를 사용하고자 한다. 다음 질문에 답하라.
(a) (x, y)를 (dx, dy)만큼 이동시키는 행렬은 무엇인가?
(b) (x, y)를 θ만큼 회전시키는 행렬은 무엇인가?
(c) 축소확대 인자가 (sx, sy)인 축소확대 행렬은 무엇인가?
- 풀이

🌱 2
- 문제
한 물체의 오브젝트 공간 기저를 {u, v, n}으로 표기하자. 회전 후에 u = (0, 0, -1), v = (1/√2, 1/√2, 0)이 되었다. 이 회전의 역변환 행렬을 계산하라.
- 풀이
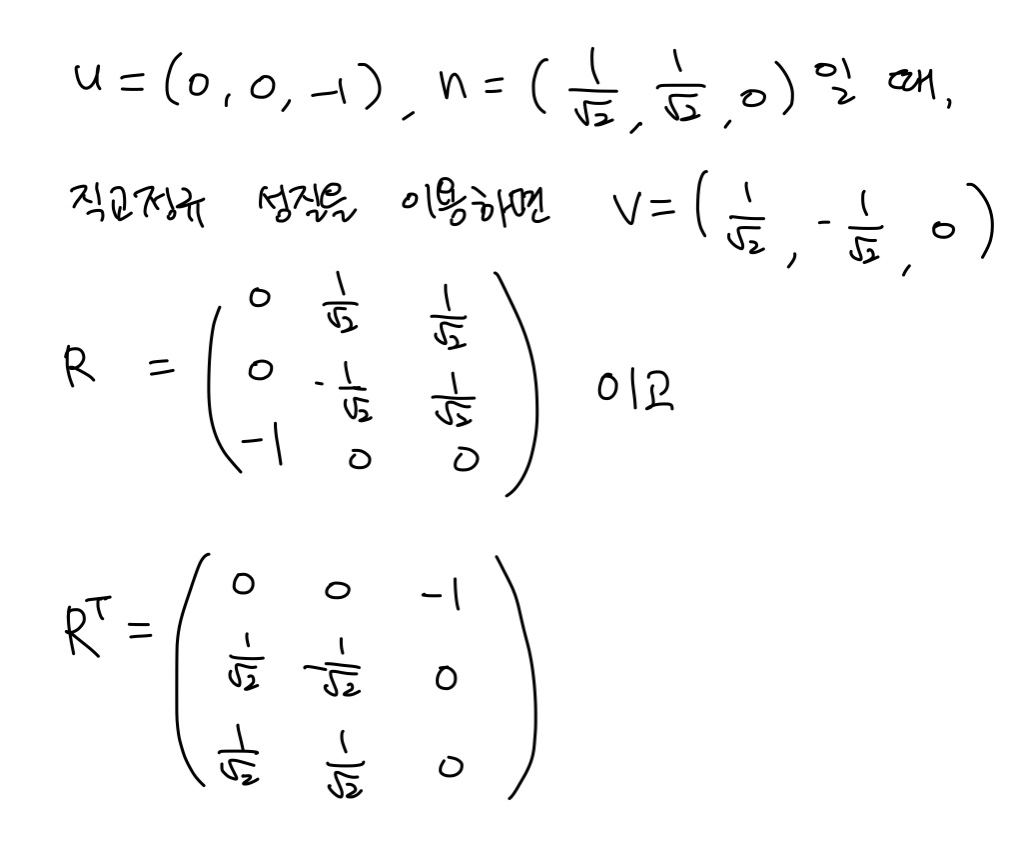
🌱 3
- 문제
아래 행렬은 회전 R에 이은 이동 T를 결합한 것이다. R과 T의 행렬을 각각 정의하라.
- 풀이
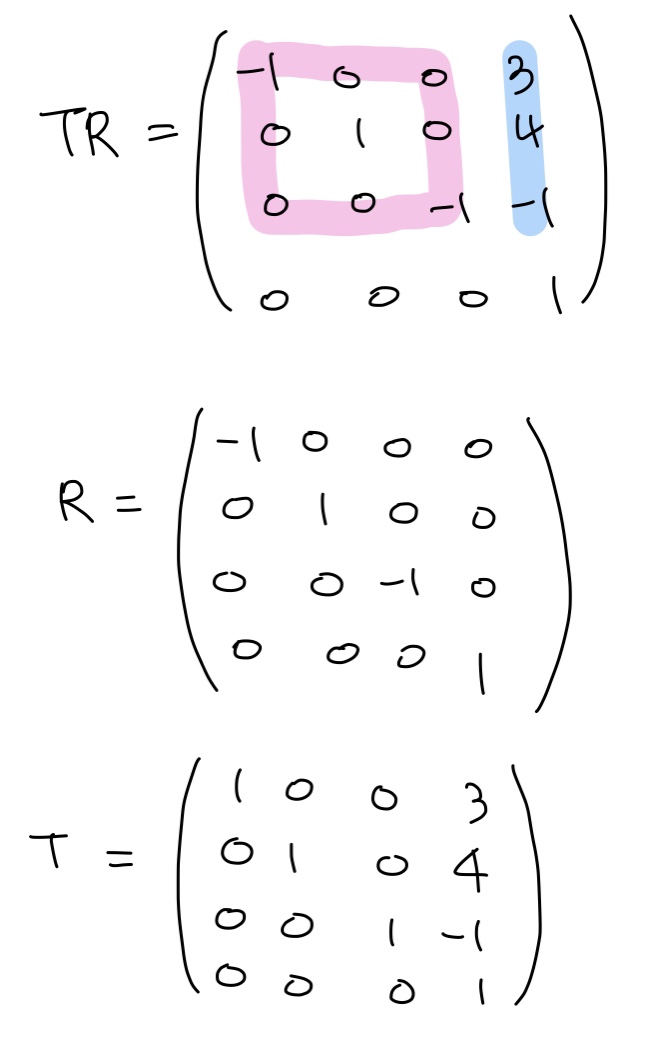
🌱 4
- 문제
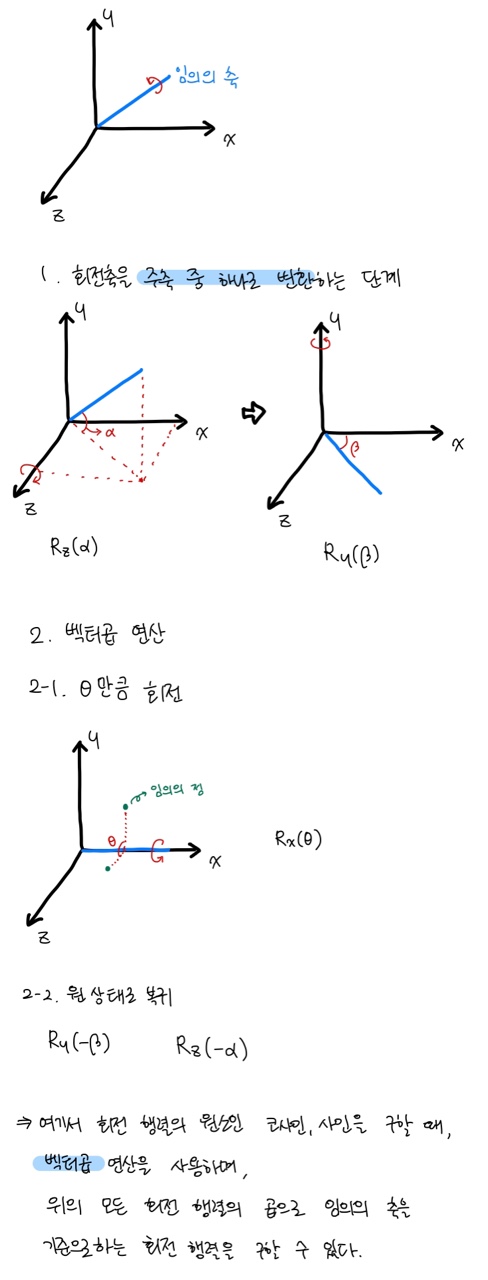
하나의 3차원 점을 임의의 축을 중심으로 θ만큼 회전시키는 순차적 과정을 설명하라. 이 과정은 회전축을 주축 중 하나로 변환하는 단계, 그리고 벡터곱(cross product) 연산을 포함해야 한다.
- 풀이
🌱 5
- 문제
다음 그림의 주전자는 (3, 0, 4)를 중심으로 90˚ 회전될 것이다. 이 같은 임의의 축 중심 회전은 세 개의 변환으로 분해된다: (1) (3, 0, 4)를 x축으로 회전, (2)를 x축 중심으로 90˚ 회전, (3) (1)의 역변환. 이 세 단계의 행렬을 각각 계산하라. [힌트: (1)을 위해 Ry(θ)를 사용하면 편리하다.]
- 풀이

🌱 6
- 문제
다음 그림의 주전자는 (3, 4, 0)을 중심으로 90˚ 회전될 것이다. 이 같은 임의의 축 중심 회전은 세 개의 변환으로 분해된다: (1) (3, 4, 0)를 x축으로 회전, (2)를 x축 중심으로 90˚ 회전, (3) (1)의 역변환. 이 세 단계의 행렬을 각각 계산하라. [힌트: (1)을 위해 Rz(θ)를 사용하면 편리하다.]
- 풀이
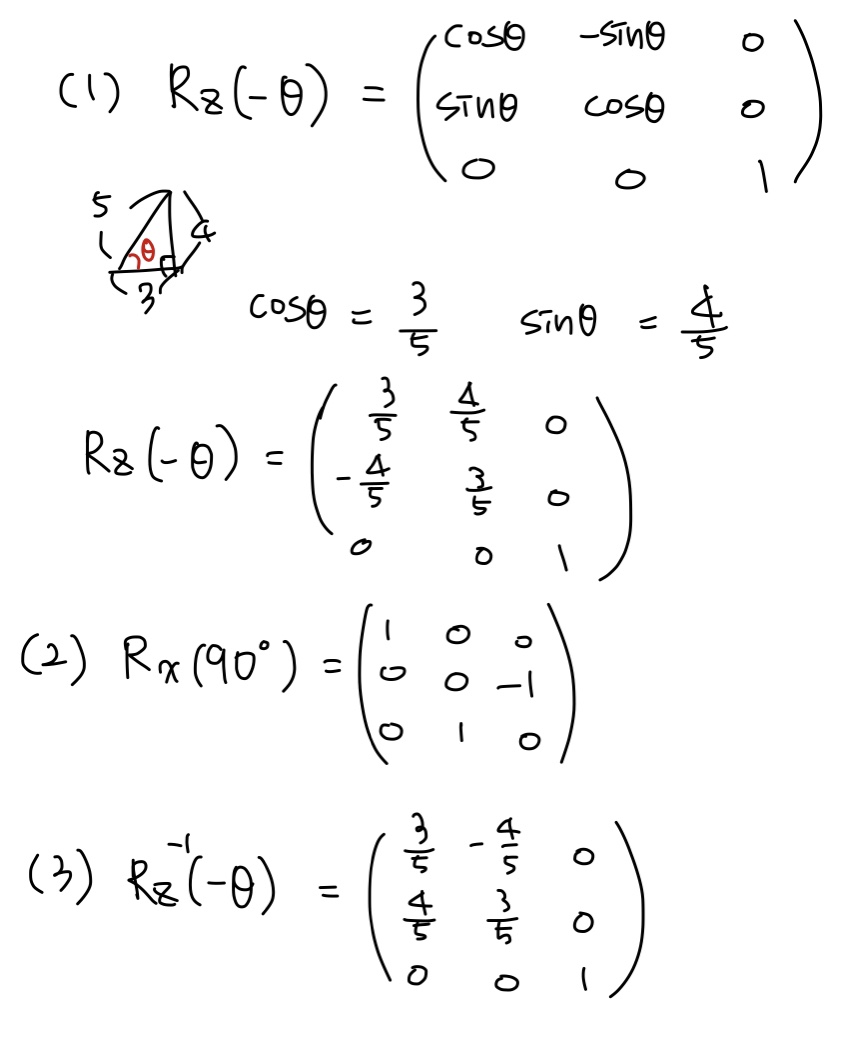
👻 글을 마치며
이번 시간에는 좌표계와 변환과 관련된 연습문제를 풀어보았다. 거진 회전을 하는 연산과 어떤 순서로 회전이 이루어지는지에 대해 연습할 수 있었던 것 같다. 확실히 주축을 기준으로 회전하는 것보다 임의의 축을 기준으로 회전하는 것이 훨씬 어려웠던 것 같다. 꾸준한 연습이 필요할 것 같다. 안 하면 금방 까먹을 것 같다 😭
출처
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음

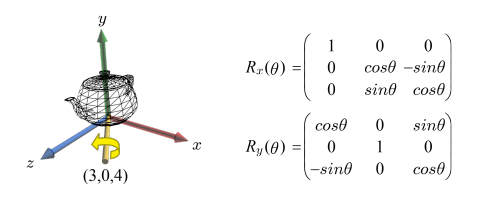
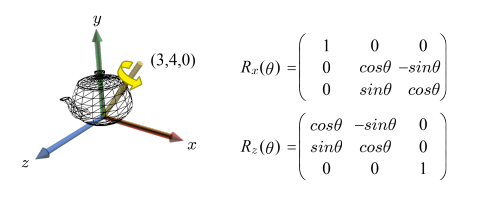
Leave a comment