[Computer Graphics] #3-1. 모델링 연습문제 풀이
👻 연습문제 풀이
3장 모델링 챕터의 연습문제는 총 6개이다.
🌱 1
- 문제
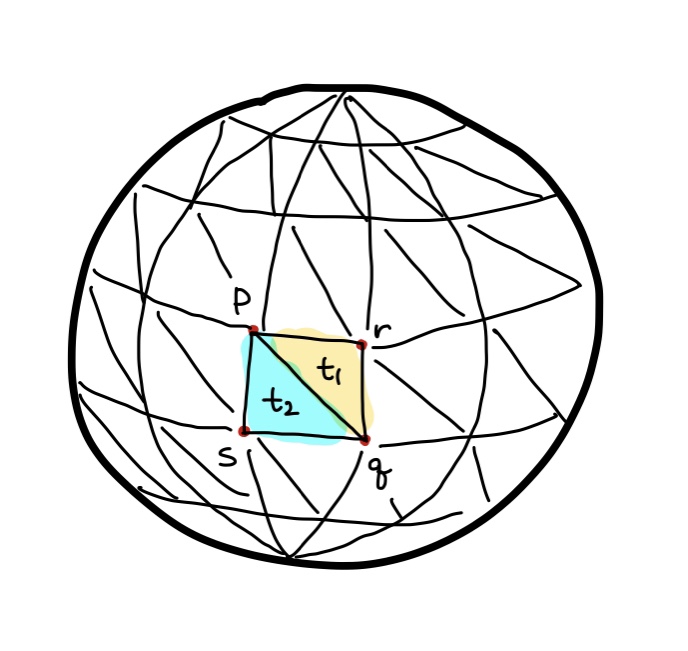
삼각형 노멀은 항상 물체 바깥쪽을 향해야 한다는 조건을 만족시키도록, 두 개의 삼각형 t1과 t2에 대한 정점 배열과 인덱스 배열을 채워라.
- 풀이
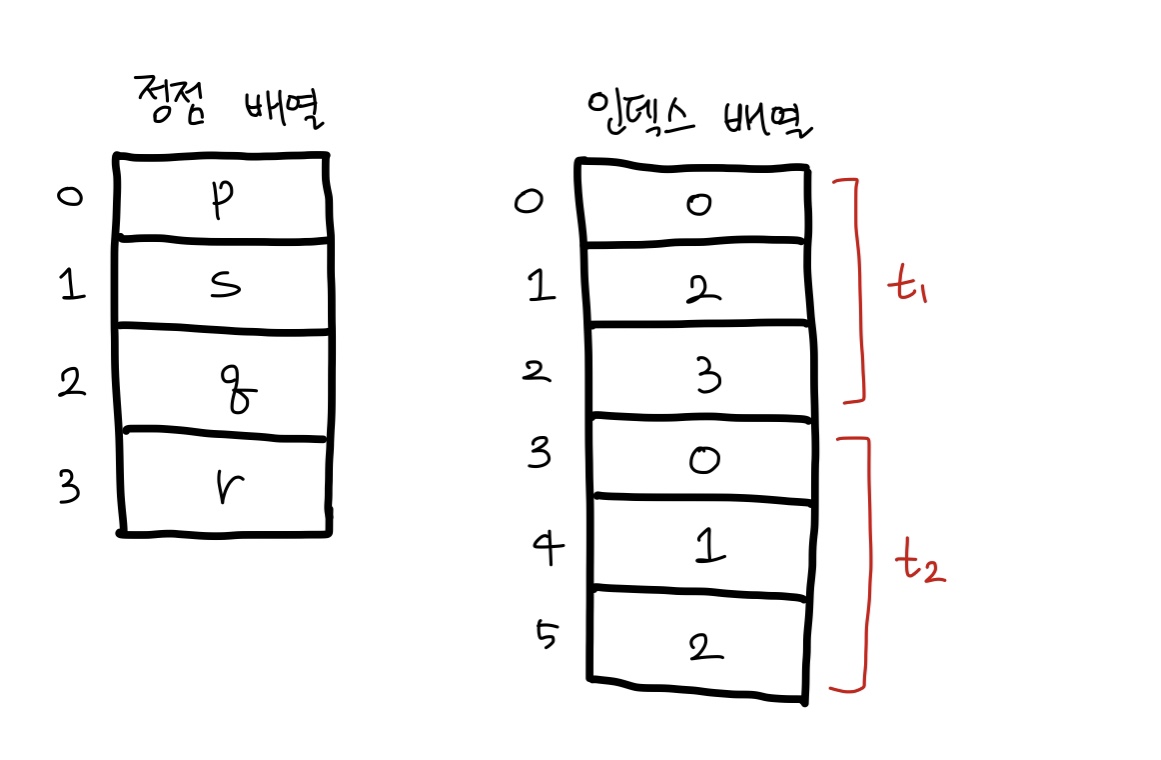
👉 정점 배열엔 모든 정점을 저장하고, 인덱스 배열은 정점의 인덱스를 정렬하여 저장한다. 삼각형 단위로 반시계 방향으로 정렬되어있어야 한다.
🌱 2
- 문제
닫힌 3차원 폴리곤 메시 중 가장 간단한 것은 사면체(tetrahedron)이다. 이를 구성하는 네 개의 정점이 (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1)이라고 가정하자. 이 사면체의 삼각형 노멀은 사면체 외부를 향해야 한다. 이 사면체를 표현하는 정점 배열과 인덱스 배열을 보여라.
- 풀이
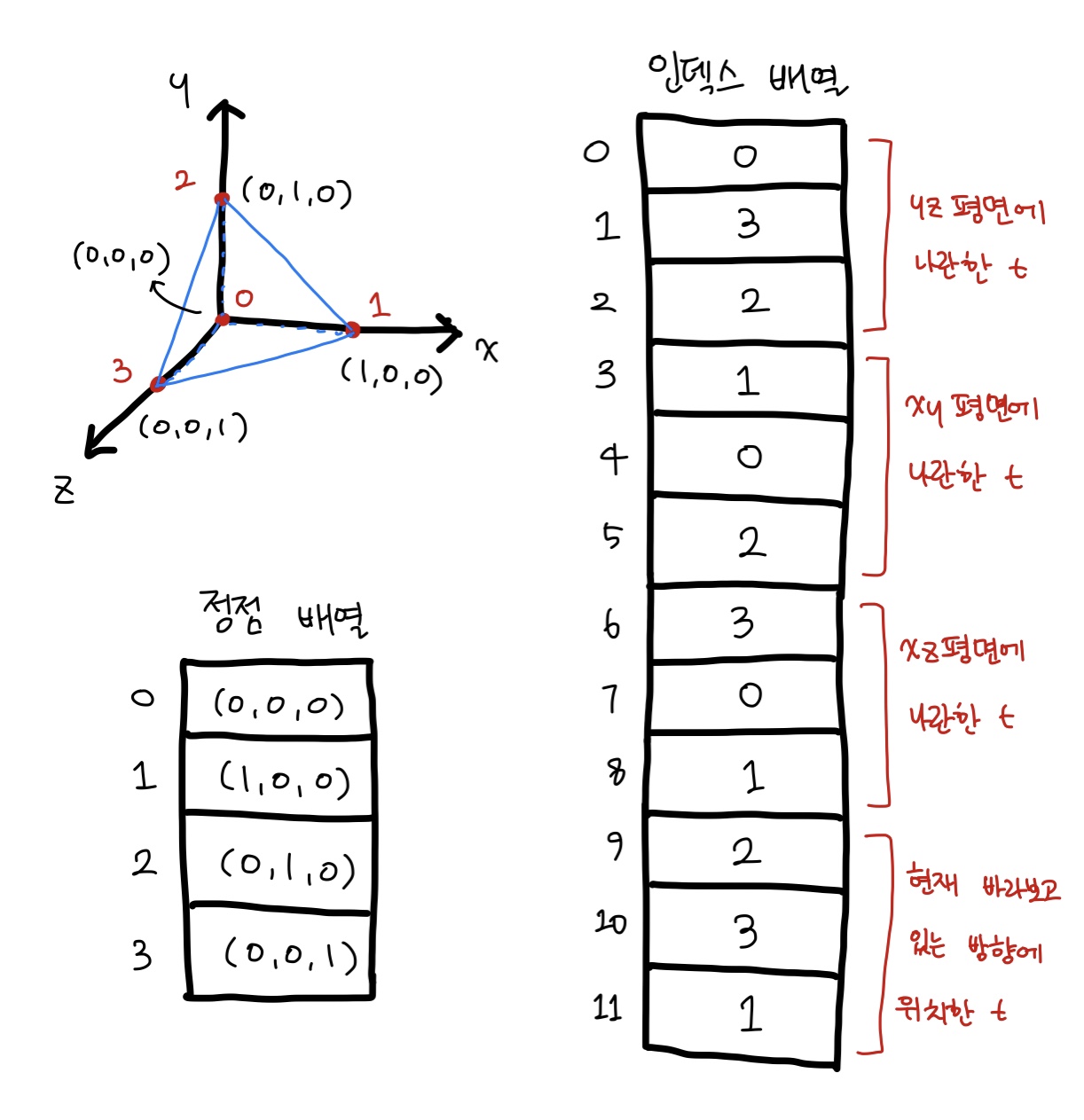
👉 사면체는 총 3개의 삼각형으로 구성되어있고 정점은 4개이다. 따라서 정점 배열은 4개의 정점 값이 들어가야 하고, 인덱스 배열은 삼각형의 개수*3 만큼 원소가 저장되어야한다.
🌱 3
- 문제
아래 그림의 메시는 8개의 삼각형으로 구성되어 있다. 인덱스 배열 없이 이 메시를 표현하는 경우, 정점 배열은 ( )개의 원소를 가진다. 반면, 인덱스 배열을 사용하여 이 메시를 표현하는 경우, 정점 배열과 인덱스 배열은 각각 ( )개와 ( )개의 원소를 가진다. 괄호 안을 채워라.
- 풀이

🌱 4
- 문제
원점에 중심을 가지는 구를 폴리곤 메시로 모델링하기 위해 위도와 경도 모두 10˚ 간격으로 정점을 정의한다고 가정하자. 이 메시의 정점은 모두 몇 개인가?
- 풀이

🌱 5
- 문제
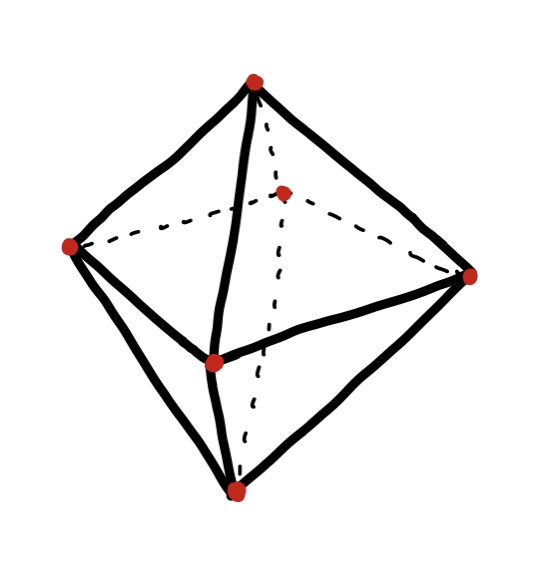
아래 그림과 같은 메시를 표현하는 정점 배열과 인덱스 배열을 채워라.
- 풀이
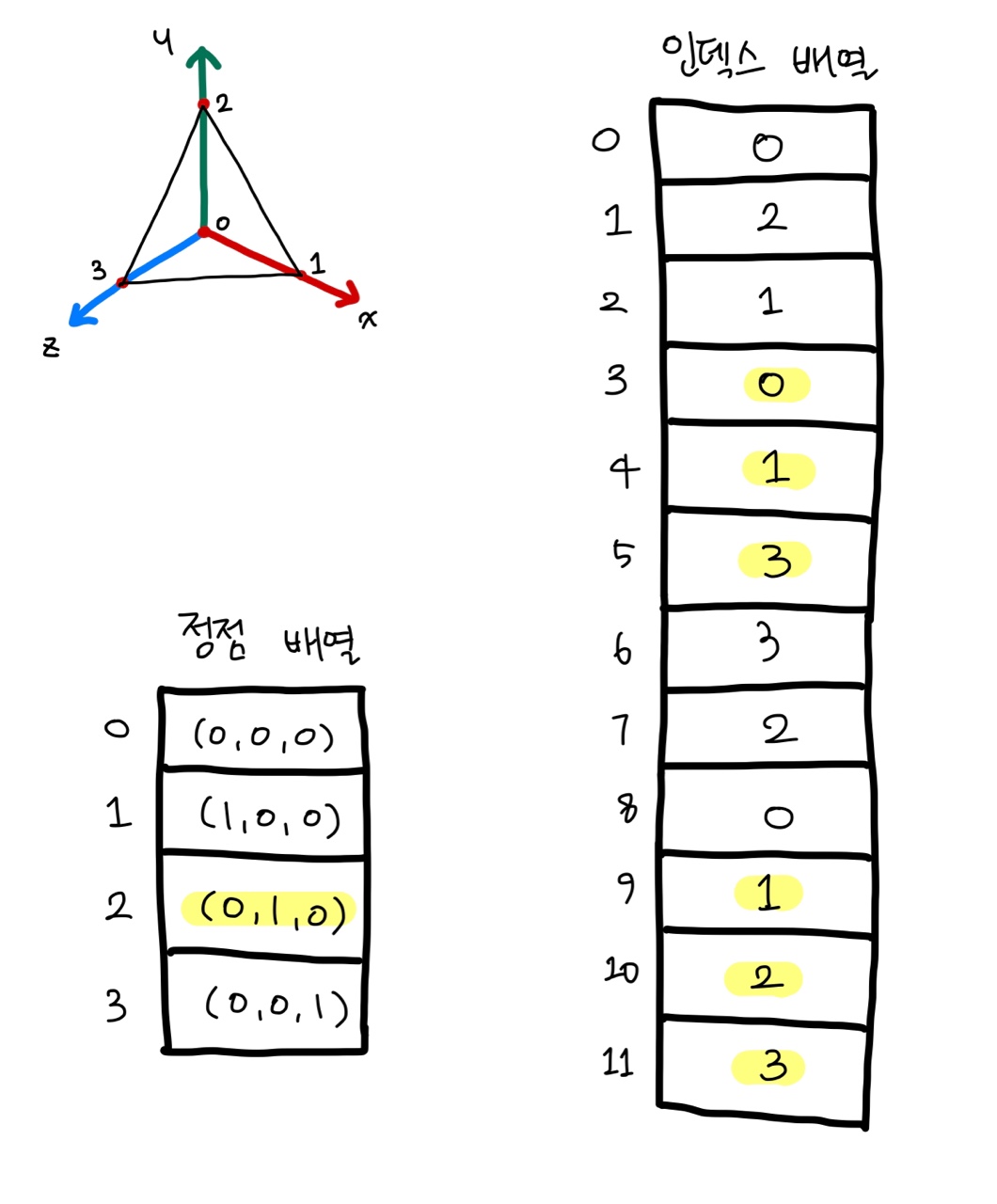
👉 2번 문제와 동일하다.
🌱 6
- 문제
닫힌 삼각형 메시에서 v, e, f가 각각 메시의 정점, 변, 면의 개수를 나타낸다고 하자. [노트: 삼각형 메시에서의 정점-삼각형 비율]에서 우리는 v와 f간 관계가 f = 2v-4임을 밝혔다. 한편, v와 e간 관계는 어떠한가?
- 풀이

👻 글을 마치며
이전 시간에 배웠던 모델링과 관련된 연습문제를 풀어보았다. 메시의 삼각형 정렬이 반시계 방향으로 되어있어야 한다는 걸 완벽히 숙지했고 정점 배열과 인덱스 배열에 어떠한 값들이 들어가는지 확실하게 알게 되었다. 4번 문제의 경우 어려워서 못 풀었다가 다른 스터디원의 도움을 통해 해결할 수 있었다. 이것이 스터디의 이유이지 않을까싶다. 😎
출처
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment