[Computer Graphics] #3. 모델링
👻 모델링
모델링은 그래픽스에서 렌더링 할 물체를 만들어내는 것이다. 가장 많이 사용되는 방식은 폴리곤 메시를 이용하는 것이다. 폴리곤 메시가 어떻게 생성되는지, 어떤 형식으로 저장되는지, 그리고 게임과 같은 런타임 응용 프로그램으로 어떻게 전달되는지 등에 대해 알아보자.
👻 폴리곤 메시
하나의 구(Sphere)를 예시로 들어 어떻게 표현할 수 있을지에 대해 알아보자. 이를 표현하는 가장 간단한 방법은 아래의 그림과 같이 f(x, y, z) = 0 형태의 음함수(Implicit Function)를 사용하는 것이다. 하지만 이러한 음함수로 표현된 물체를 스크린에 렌더링하는 것은 쉽지 않다. GPU가 음함수를 처리하기에 적합하게 설계되어있지 않기 때문이다.
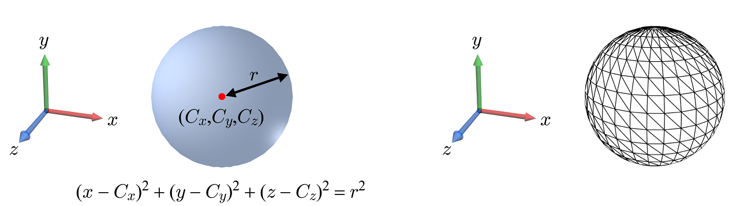
이러한 음함수 표현 대신 부드러운 표면의 점들을 샘플(Sample)하면 정점(Vertex)이 나오게 된다. 이 정점을 이으면 폴리곤 메시가 된다. 폴리곤 메시처럼, 정점 및 폴리곤과 같은 요소들을 명시적으로 정의하여 구를 표현할 수도 있다. 폴리곤 메시는 정확한 표현법이 아닌 근사적 표현법임을 알아두자.
가장 간단한 폴리곤은 삼각형이다. 삼각형으로만 구성된 메시를 삼각형 메시(Triangle Mesh)라고 하며, OpenGL은 삼각형 메시만 처리한다. 하지만 모델링 작업을 위해서는 사각형 메시(Quadrilateral Mesh 혹은 간단히 Quad Mesh)가 선호된다(맥스나 마야는 사각형 메시를 사용하는 것이 유용하다). 사각형 메시를 삼각형 메시로 바꾸는 가장 간단한 방법은, 각 사각형을 두 개의 삼각형으로 분할하는 것이다.
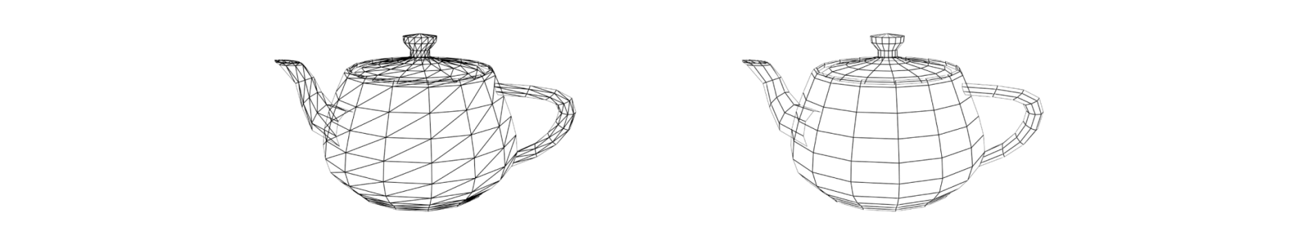
일반적인 닫힌 메시(Closed Mesh)에서 삼각형의 개수는 정점 개수의 두 배 정도이다.
💡 삼각형 메시에서의 정점-삼각형 비율
오일러 공식(Euler’s Polyhedron Formula)을 이용하여 식을 구하면 다음과 같다.v - e + f = 2여기에서 v, e, f는 각각 메시의 정점, 변, 면의 개수이다. 닫힌 삼각형 메시에서 하나의 변은 두 개의 면에 의해 공유되고, 하나의 면은 세 개의 변을 가진다. 변을 하나씩 방문하면서 그를 공유하는 면 두 개에 표시를 남기면, 모든 변 방문이 마쳐졌을 때에는 각각의 면에 세 개의 표시가 남게 된다.
2e = 3f위의 오일러 공식에 방금 나온 공식을 치환하면 다음과 같은 결과를 얻을 수 있다.
f = 2v - 4따라서, 메시의 크기가 커질수록 면의 개수 f는 정점의 개수 v의 2배에 수렴한다.
🌱 Levels of Detail
폴리곤 메시는 부드러운 곡면을 근사적으로 표현한 것이다. 따라서 얼마나 많은 정점을 사용하여 근사할 것인가는 중요한 문제가 된다. 보통 정점의 개수를 우리가 흔히 아는 해상도(Resolution)로 표현이 된다. 또는 Levels of Detail(LOD)로도 불린다. 정점의 개수가 많으면 해상도가 높다고 말하며, 정점의 개수가 적으면 해상도가 낮다고 표현한다.
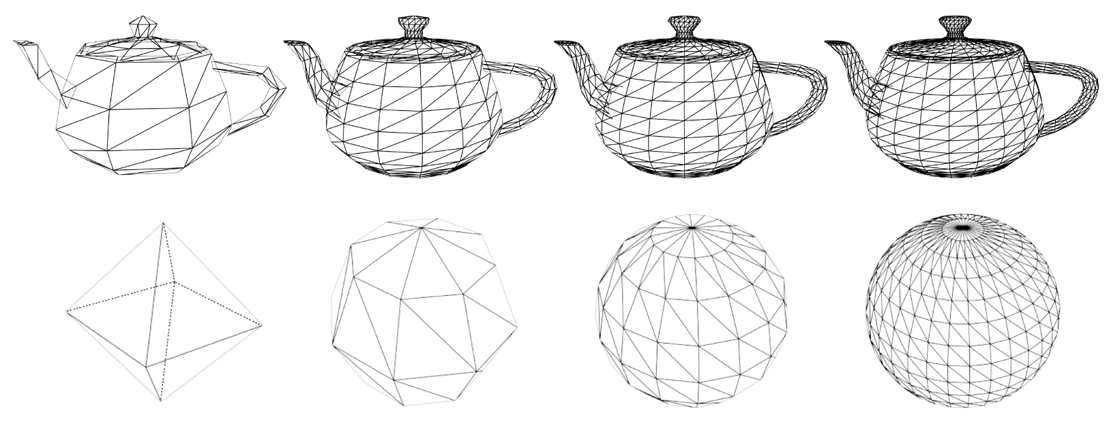
정점의 개수가 많아질수록 해상도가 높아지는 Refinement, 정점의 개수가 적어질수록 해상도가 낮아지는 Simplification 과정을 거친다. 실제로 화면상에 물체가 어느 정도의 크기로 나올것인지에 따라 달라질 수 있다. 화면상에 아주 작은 물체로 나오지만 쓸데없이 해상도가 높으면 메모리를 많이 차지하게 될 것이다.
🌱 폴리곤 메시 표현
폴리곤 메시가 컴퓨터 안에서 어떤식으로 표현이 되는지에 대해 알아보자. 삼각형 메시에서 삼각형을 구성하는 세 개의 정점을 순서대로 나열하는 방법을 이용하면 가장 단순하게 삼각형 메시에 대한 정보를 저장할 수 있을 것이다.
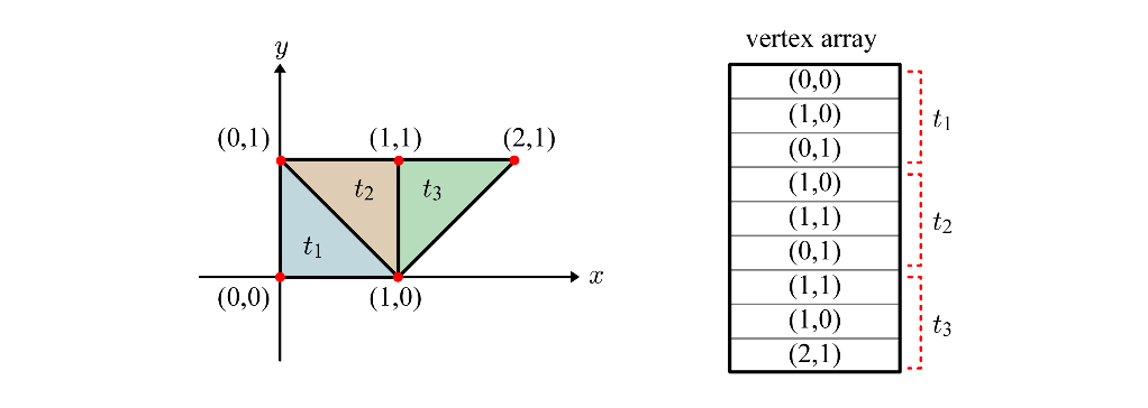
위의 이미지처럼, 정점의 정보를 정점 배열(Vertex Array)에 삼각형 단위로 저장한다. 하지만 이러한 저장방식은 중복된 데이터가 많아지는 문제점이 있다. 고로 좋은 표현법은 아니다. 이러한 문제점을 해결할 수 있는 방법으로 인덱스 배열(Index Array)을 정점 배열과 함께 사용한다.
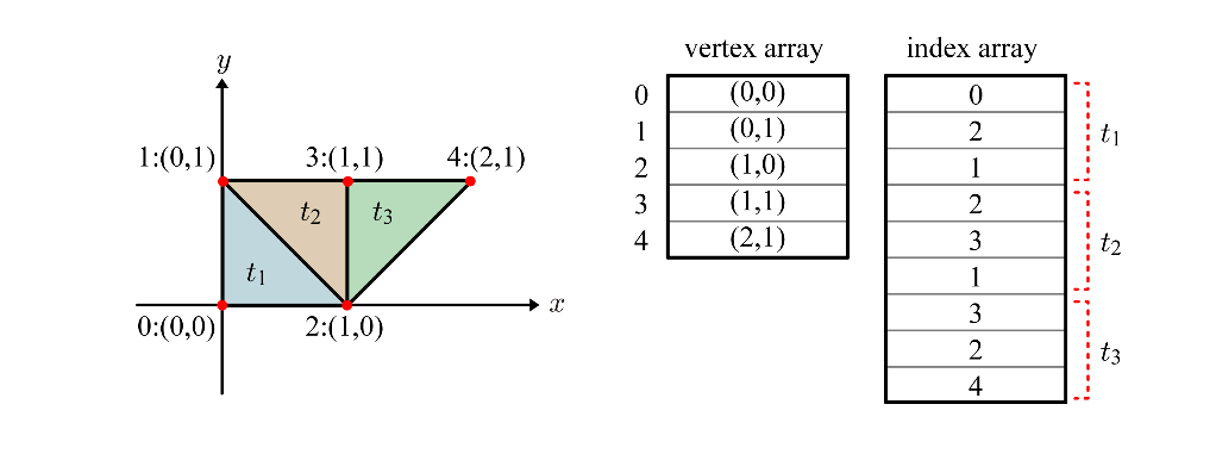
정점 배열에는 정점의 정보만 중복없이 저장해두고, 인덱스 배열(Index Array)를 따로 만들어 정점의 인덱스 정보만을 담는다. 이 방법이 삼각형 메시를 컴퓨터에서 표현하는 가장 일반적인 형태이다.
💡 배열이 많아졌는데 오히려 메모리 낭비가 아닐까?
낭비인 것 같지만 그렇지 않다. 인덱스 배열은 2바이트나 4바이트로 표현할 수 있을 정도의 작은 크기를 가진다. 반면, 정점 배열의 한 셀은 해당 정점에 대한 모든 정보(포지션, 노멀 등)가 들어있기 때문에 용량이 아주 크다. 정점 배열에서 중복된 데이터를 제거하여 절약되는 정점 배열 공간은 인덱스 배열이 차지하는 공간 크기를 능가하게 된다.
👻 Surface Normals
표면 노멀(Surface Normal)은 3차원 물체를 렌더링할 때 핵심적인 역할을 한다. 노멀은 표면에 수직인 법선 벡터를 의미하며 정점의 포지션 외의 정보 중 하나에 속한다.
🌱 삼각형 노멀
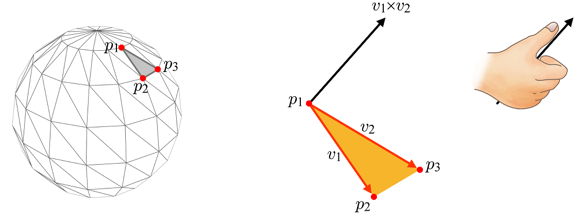
오른손 법칙을 적용하여 벡터곱을 구하고 정규화를 하면 삼각형 노멀을 구할 수 있다. 삼각형 노멀은 삼각형 표면에 대하여 수직인 법선 벡터를 의미한다.
삼각형 정점의 순서가 바뀌게 되면 노멀의 방향은 어떻게 될까? 우선, 위에서 본 이미지의 정점 순서는 삼각형의 반시계 방향(Counter-Clockwise: CCW)으로 정렬되어있다. 정점의 순서를 바꿔 삼각형의 시계 방향으로 정렬하게 되면, 삼각형 노멀의 방향도 반대로 바뀌게 된다. 폴리곤 메시의 안쪽으로 향하게 되는데, 그래픽스에서는 모든 노멀이 물체의 밖을 향하는 것이 기본적인 관례이다. 따라서 정점의 순서가 반시계 방향으로 항상 정렬되어있도록 주의해야한다.
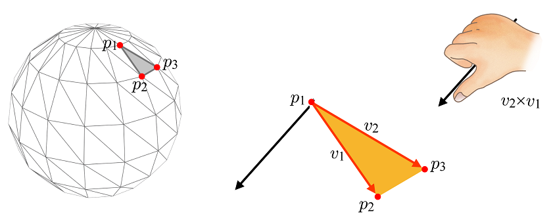
정점의 순서가 바뀌며 노멀의 방향도 바뀐 것을 알 수 있다.
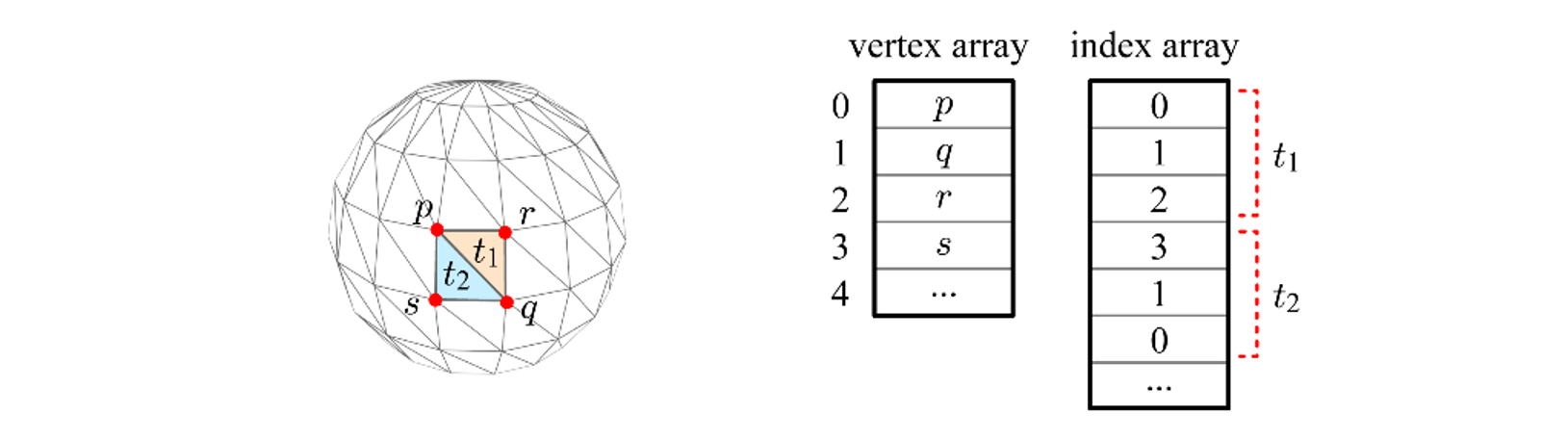
인덱스 배열에 삼각형 정보를 저장할 때 항상 반시계 방향으로 정렬되어있어야 함을 주의해야한다.
🌱 정점 노멀
정점 노멀은 삼각형 노멀과 달리 정점에 대한 노멀을 의미한다. 부드러운 표면에서 Tangent Plane(기울기)을 구할 수 있고, 여기에 수직인 벡터를 정점 노멀이라한다.
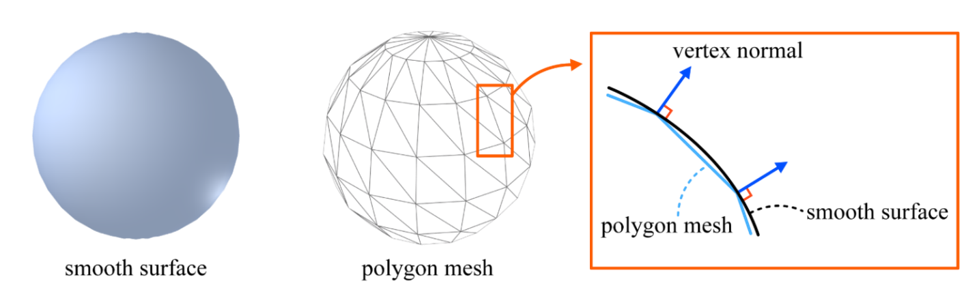
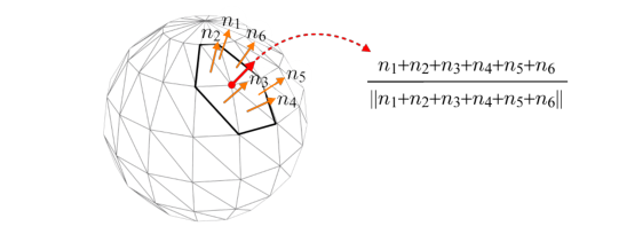
부드러운 표면이 주어지지 않고 오로지 폴리곤 메시만 존재한다면 해당 정점을 공유하는 삼각형 노멀의 평균을 내는 방식으로도 구할 수 있다(프로그램이 해준다). 하지만 부드러운 표면이 주어지지 않았을 때 정점 노멀을 구하는 방식엔 정답이 딱히 존재하지 않는다.
만약, 맥스에서 모델링을 하게 된다면 비록 모든 것을 수동으로 만들지만 노멀은 자동으로 만들어진다. 또한 컴퓨터 그래픽스에서 실제로 중요한 것은 정점 노멀이며 정점 배열이 포지션을 더하여 반드시 가져야 할 정보이다. 해당 노멀은 라이팅(Lighting)에 필수적이기 때문이다.
👻 Export and Import
하나의 응용에서 만들어진 데이터를 다른 응용에 적합한 형태로 출력하는 과정을 내보내기 혹은 익스포트(Export)라 부르고, 이렇게 출력된 데이터를 읽어오는 과정은 불러오기 혹은 임포트(Import)라 한다. 해당 과정을 수행하기 위해서는 간단한 프로그램이나 스크립트를 사용한다. 맥스같은 경우 해당 프로그램이 제공하는 MAXScript를 이용하면 쉽게 진행할 수 있다.
맥스가 지원하는 대표적인 파일 포맷 중 하나는 .obj이다. 이는 기본적으로 정점 위치와 노멀, 그리고 삼각형 정보를 저장하는데, 정점 위치는 vertex의 앞 글자 v, 정점 노멀은 vertex normal의 앞 글자 vn, 삼각형은 face(면)의 앞 글자 f를 기호로 사용한다.

구 같은 경우 정점마다 노멀의 값도 다르기 때문에 정점의 개수만큼 정점 노멀을 가지게 될 것이다. 하지만 정점 노멀의 값이 같은 경우엔 중복하여 겹쳐쓰지 않기 때문에 정점의 개수보다 적을 수도 있다.
삼각형 정보에는 각 정점의 정보를 알려줘야한다. 슬래시 두 개(//)로 구분하여 사용하고 슬래시 앞 부분은 정점 위치, 뒷 부분은 정점 노멀을 의미한다.
v//vn
파일이 임포트되면 정점 배열과 인덱스 배열이 파일 정보를 바탕으로 생성될 것이다.

👻 글을 마치며
이번 시간에는 모델링에 대해 알아보았다. 파일이 어떤 방식으로 저장이 되고 계산이 되는지 알 수 있었다. 생각보다 간단하게 구성할 수 있을 것 같았는데 의외로 많은 정보가 저장이 되고 구조가 복잡하다고 느꼈다. 아무래도 방향이라는 변수가 있기 때문에 한 번에 계산하기가 쉽지 않아서 그렇지 계산 방법만 익숙해지면 파일을 분석하는 데에는 큰 어려움이 없을 것 같다.
출처
한정현 컴퓨터 그래픽스 강의 (3장-모델링)
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment