[Computer Graphics] #2-1. 수학 기초 연습문제 풀이

👻 연습문제 풀이

2장 수학 기초 챕터의 연습문제는 총 2개이다.

---

🌱 1

• 문제

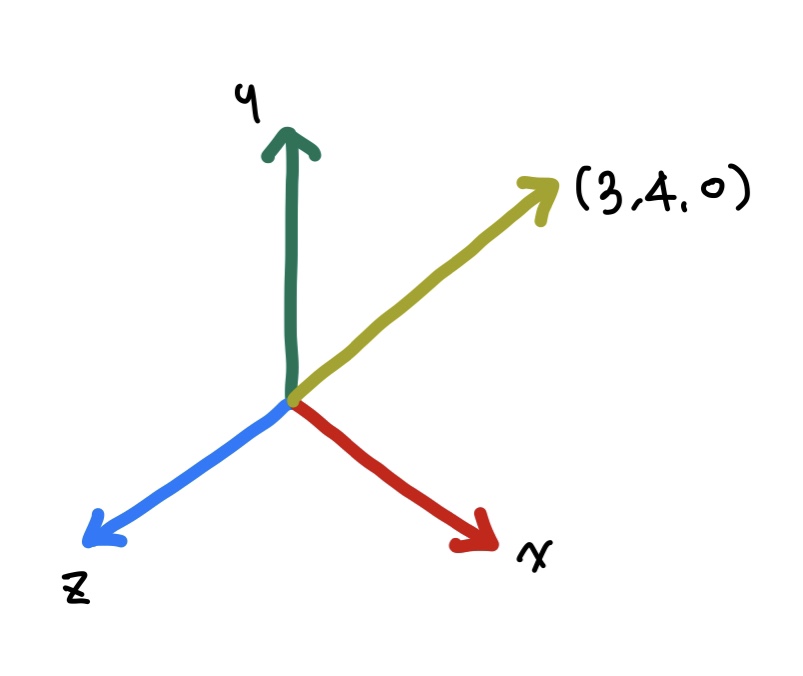
3차원 직교정규 기저를 생각해 보자. 첫 번째 기저 벡터는 아래 그림과 같이 (3, 4, 0) 방향을 향하고, 두 번째는 하나의 주축을 향하며, 세 번째는 그 둘의 벡터곱으로 정의된다. 이 기저를 계산하라.

• 풀이

👉 첫 번째로 주어진 벡터를 정규화 시켜서 기저를 구하였다. 두 번째로는 해당 기저와 수직이어야 한다. 첫 번째 기저는 xy 평면에 위치하며 해당 기저와 수직이려면 z축과 나란해야한다. 그래서 (0, 0, 1) 벡터를 두 번째 기저로 구하였다. 마지막은 위의 두 기저를 벡터곱한 (4/5, -3/5, 0)이 된다.

---

🌱 2

• 문제

두 개의 점 p₀와 p₁이 있다. p₀의 좌표는 (2, 0)이고 p₁의 좌표는 (5, 0)이다. p₀에 벡터 (-1, 2)가 저장되어 있고, p₁에는 벡터 (2, 5)가 저장되어 있다. p₀와 p₁을 잇는 선분을 따라 두 벡터를 선형보간할 때, 선분 위의 점 (4, 0)에 놓일 벡터를 계산하라.

• 풀이

---

👻 글을 마치며

이전 시간에 배웠던 수학 기초와 관련된 연습문제를 풀어보았다. 오랜만에 문제를 푸는 것이기도 하고 익숙치 않은 분야다보니 처음엔 조금 당황했지만 그래도 응용한다 생각하니 쉽게 풀 수 있었다. 연습문제 2번 선형보간과 관련된 주제는 생각보다 헷갈리는 부분이 많아서 개념을 한 번 더 확실하게 잡아야 할 것 같다.

---

출처
도서 관련 예제 GitHub
PPT 강의 자료

관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음