[Computer Graphics] #2. 수학 기초
👻 행렬과 벡터
행렬과 벡터는 선형 대수의 기본이 되는 내용이다. 간단하게 알아보도록 하자.
🌱 행렬
행렬(Matrix)은 이름 그대로 행(Row)과 열(Column)로 구성된다. 다음은 m개의 행과 n개의 열을 가진 행렬이다.
이 행렬의 크기는 m × n으로 표기되는데, m과 n이 같다면 정사각행렬(Square Matrix)이라 한다.
🪐 행렬의 곱셈
두 행렬의 곱셈식은 다음과 같다.
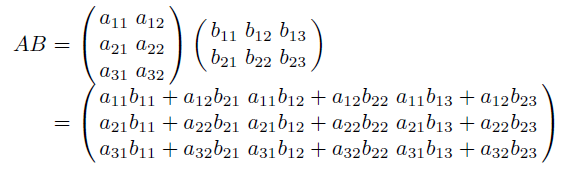
A의 크기가 l × m이고, B의 크기가 m × n이라면, AB의 크기는 l × n이 된다.
💡 좌측 행렬의 열의 개수와 우측 행렬의 행의 개수가 동일해야 두 행렬간의 곱셈이 가능하다.
🌱 벡터
벡터(Vector)는 특수한 행렬이다. 2차원 벡터는 (x, y)로, 3차원 벡터는 (x, y, z)로 표기된다. 이렇게 표기된 벡터를 행벡터(Row Vector)라고 부른다. 이와 달리 열벡터(Column Vector) 표기법을 쓸 수도 있다.
💡 열벡터(Column Vector) 표기법
2차원 열벡터
3차원 열벡터
💡 행렬-행렬 곱셈 방법은 행렬-벡터 곱셈에 그대로 적용된다.
🌱 전치 행렬
어떤 행렬 M이 주어졌을 때, 그것의 행과 열을 바꿔놓은 것을 전치 행렬(Transpose Matrix)이라고 하며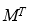 
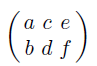
로 표기한다.
이는 벡터에도 그대로 적용된다. 열벡터의 전치 행렬은 행벡터가 된다. 이를 이용하여 행벡터를 사용한 행렬-벡터 곱셈은 방법은 동일하지만 행벡터가 전치 행렬의 왼쪽에 위치해야한다.
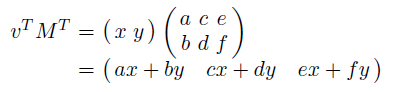
💡 OpenGL은 열벡터를 사용하고, Direct3D는 행벡터를 사용한다.
🌱 단위 행렬
단위 행렬(Identity Matrix)는 정사각행렬 중, 왼쪽 위 끝과 오른쪽 아래를 잇는 대각선에 놓인 원소는 모두 1이고 나머지 원소는 모두 0인 경우를 말하며 이는 I로 표기한다.
-
2 × 2단위 행렬
-
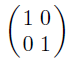
3 x 3단위 행렬
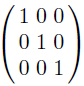
임의의 행렬 M에 대해서, 다음과 같이 MI = IM = M이 성립한다.
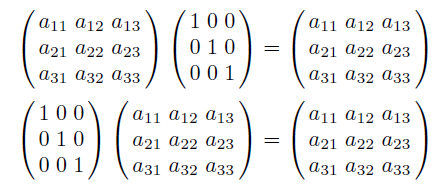
🌱 역행렬
두 개의 정사각행렬 A와 B가 곱해져서 그 결과가 I가 된다면, B는 A의 역행렬(Inverse Matrix)이라고 부르며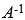 
로 표기한다. 반대도 마찬가지이다.
💡 이와 유사하게 두 행렬의 곱셈의 전치 행렬도 구할 수 있다.
🌱 단위 벡터
2차원 벡터 v의 좌표를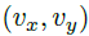 
로 표현할 때, v의 길이는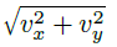 
으로 정의되고 ||v||로 표기된다. 3차원 벡터도 마찬가지이다.
이러한 벡터 v를 그 길이 ||v||로 나누는 과정을 정규화(Normalization)라고 하는데,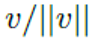 
는 v와 같은 방향을 가지며 길이가 1인 벡터이다. 이를 단위 벡터(Unit Vector)라고 부른다.
👻 좌표계와 기저
이제 그래픽스에 필요한 수학인 좌표계와 기저에 대해 알아보자. 우선 좌표계(Coordinate System)는 원점(Origin)과 기저(Basis)로 이루어져있다. 그래픽스에선 좌표계를 간단하게 공간(Space)라고 한다.
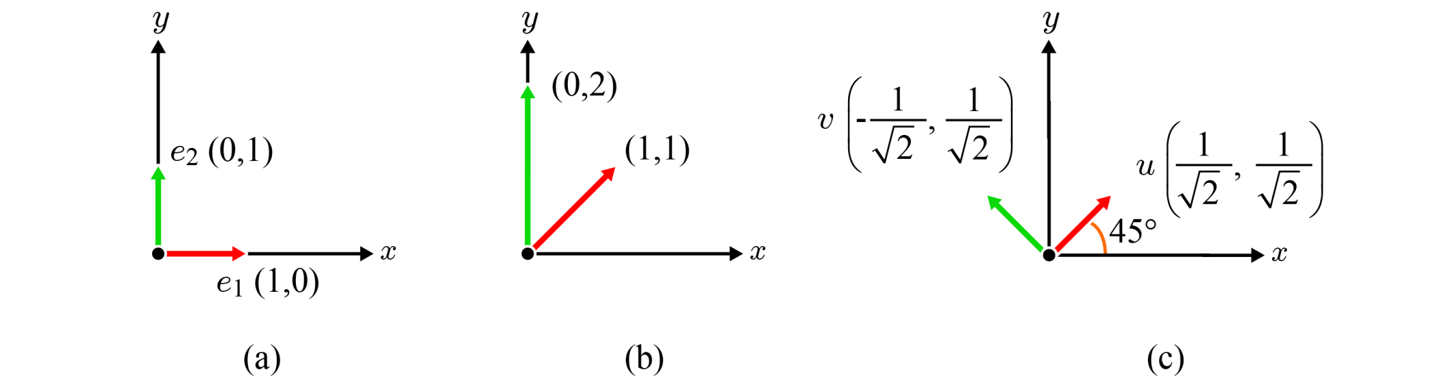
2차원 좌표계에서, x축에 나란한 벡터 e₁은 (1, 0)이고, y축에 나란한 벡터 e₂는 (0, 1)이다. 2차원 공간의 모든 벡터는 위의 두 벡터의 선형 조합(Linear Combination)으로 표현이 가능하다. 이러한 점에서 두 벡터를 기저(Basis)라고 부르며, 두 벡터가 주축(Principal Axis)에 나란하므로 특별히 표준 기저(Standard Basis)라고 한다. 또한, 두 벡터는 서로 직교하는 단위 벡터이므로 직교 정규(Orthonormal) 성질을 가진다고 말한다.
💡 직교 정규(Orthonormal)
- 수직을 의미하는 Orthogonal과 정규화를 의미하는 Normalized의 복합어이다.
- 벡터가 서로 수직이고 단위가 1인 단위 벡터를 의미한다.
3차원 공간에서의 표준 기저는 다음과 같다.
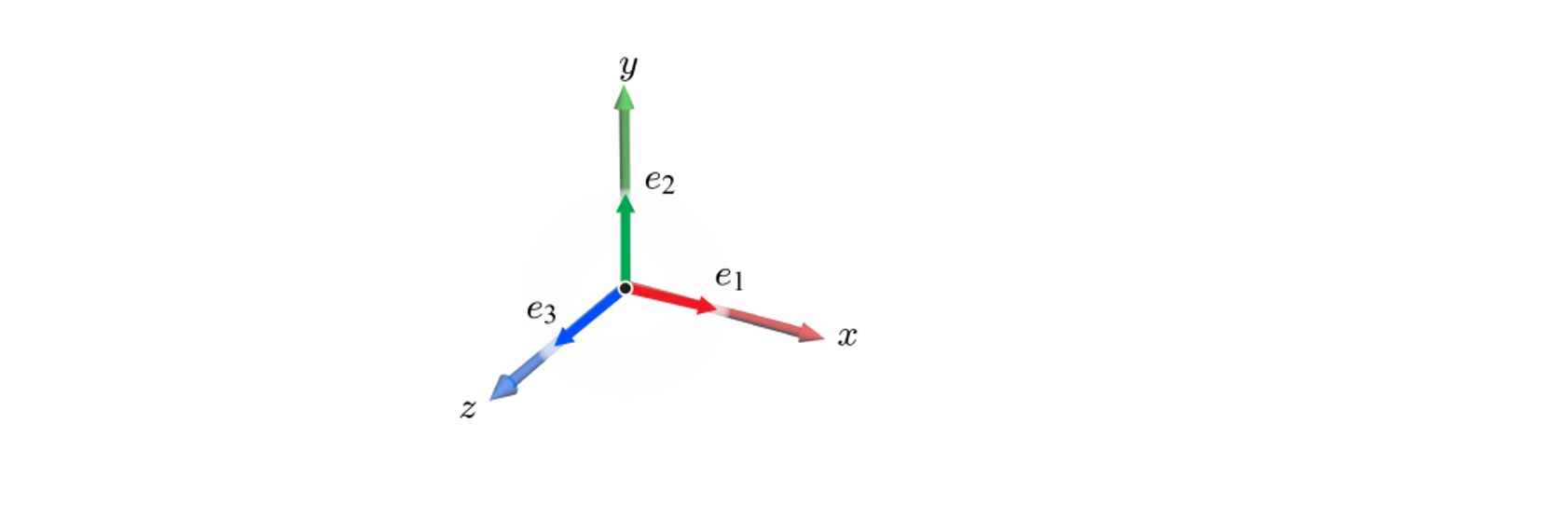
세 개의 주축에 나란한 e₁, e₂, e₃는 각각 (1, 0, 0), (0, 1, 0), (0, 0, 1)이며 물론 직교정규 성질을 가진다.
👻 내적
내적(Dot Product 또는 Inner Product)은 벡터 연산 중 하나로 다음과 같이 정의된다.
a·b = a₁b₁ + a₂b₂ + … + anbn
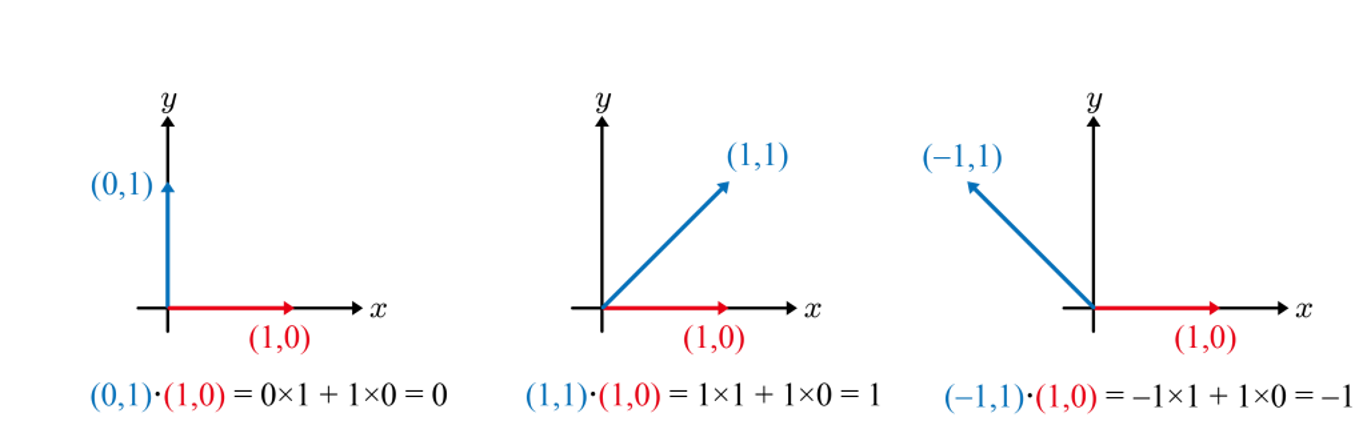
두 벡터 a와 b 사이의 각도를 θ로 표기하면 기하학적으로는 다음과 같이 정의된다.
a·b = ||a||||b||cosθ
θ가 예각이라면 양수, 둔각이라면 음수다. 여기서 하나의 단위 벡터를 자기 자신과 내적하면 1이 된다(θ가 0이되고, cos0˚는 항상 1이기 때문이다).
하나의 직교정규 기저가 있을 때, 동일한 기저 벡터 간 내적은 1이고, 다른 기적 벡터 간 내적은 0이다(cos90˚ = 0). 이는 2차원은 물론 3차원의 모든 직교정규 기저가 가지는 성질이다.
배타적인 성격을 가진다.
👻 벡터곱
두 개의 3차원 벡터 a와 b의 벡터곱(Cross Product)은 a × b로 표기된다. 벡터곱은 3차원 공간에서만 정의되며 벡터곱의 결과로 또 다른 3차원 벡터가 만들어진다. 벡터의 방향은 오른손 법칙(Right-Hand Rule)을 통해 정해진다.
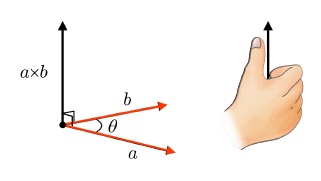
네 손가락이 a에서 b로 움직일 때 엄지의 방향이 벡터곱 결과의 방향을 의미한다. 해당 벡터의 길이는 다음과 같이 정의할 수 있다.
||a||||b||sinθ
a × b의 길이는a와b에 의해 만들어지는 평행사변형의 넓이와 같다.
여기서 a = b이면 모든 값이 0인 제로 벡터(Zero Vector)가 만들어진다. 또한, a와 b의 순서를 바꾸게 되면 길이는 같지만 방향이 정반대인 벡터가 만들어진다. 이런 점에서, 벡터곱을 반가환적(Anti-Commutative)이라 부른다.
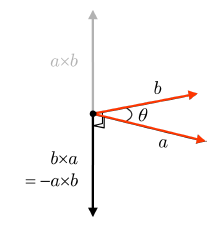
b x a = -a x b
벡터곱의 계산은 다음과 같다.
💡 각도별 벡터곱 결과
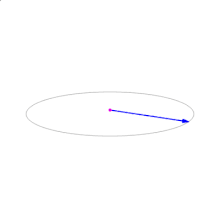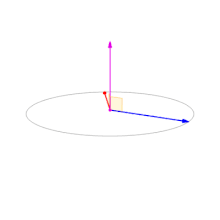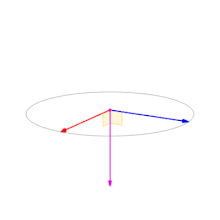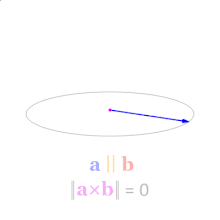
출처 : 위키피디아 Cross Product
👻 직선 및 선형 보간
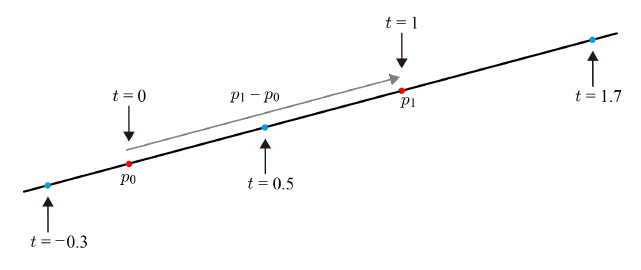
어떠한 직선이 있고, 두 개의 점 p₀와 p₁을 지난다고 가정하자. 둘을 잇는 벡터는 p₁ - p₀로 표현할 수 있고, 이 벡터를 사용하여 다음과 같은 매개변수 방정식(Parametric Equation)으로 정의된다.
여기서 t는 [-∞, ∞] 범위에 놓이는 매개변수이며 p(t)는 양쪽으로 무한히 뻗은 직선을 표현한다.
만약 t의 범위가 [0, ∞]라면, p(t)는 p₀에서 시작하여 p₁ - p₀ 방향으로 무한하게 뻗어나가는 광선(Ray)이 된다.
마지막으로 t의 범위가 유한하게 한정된다면, p(t)는 선분을 표현하게 될 것이다.
위의 식을 다시 쓰면 다음과 같다.
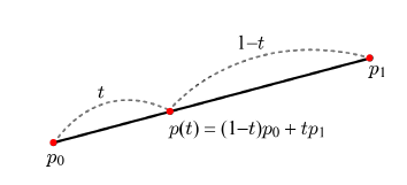
위 식에서 (1-t)와 t를 각각 p₀와 p₁에 대한 가중치(Weight)로 보면, p(t)는 p₀와 p₁의 가중치 합(Weighted Sum)이 된다.
특히, t의 범위가 [0, 1]일 때, p(t)는 p₀와 p₁의 선형 보간(Linear Interpolation)이라고 한다.
💡 Interpolation
- 알려진 지점의 값 사이(중간)에 위치한 값을 알려진 값으로부터 추정하는 것
3차원 좌표에서의 선형 보간법은 다음과 같이 적용할 수 있다.
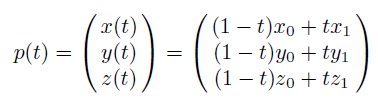
만약, p₀와 p₁에 특정한 값이 저장되어 있다면, 그 값들도 선형 보간될 수 있다. 예를 들어 색상을 표시하는 값 중 RGB에 대해 생각해보면 다음과 같이 나타낼 수 있다.
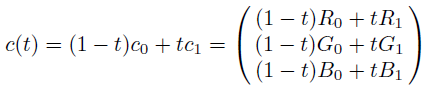
RGB 원소 각각은 대개 [0, 255] 범위의 정수값, 혹은 [0, 1] 범위의 실수값을 가지는데, 위의 벡터에서, t가 0이면 c(t)는 c₀가 되고, t가 증가할수록 c(t)는 c₁에 가까워지며, t가 1이 되면 c(t)는 c₁이 된다.
👻 글을 마치며
이번 시간에는 그래픽스와 관련된 선형 대수학의 기초에 대해 알아보았다. 언리얼을 조금 해보면서 좌표값(벡터값)이 중요하다는 건 알고 있었는데 정확히 이 기초가 게임을 제작할 때 어떠한 방식으로 적용되어있는지는 아직까진 감이 잡히지 않는다. 아무래도 직접 그래픽스를 건드려보고 구현해봐야 어떤 식으로 적용이 되어있는지 알 수 있을 것 같다.
출처
한정현 컴퓨터 그래픽스 (2장-수학 기초)
도서 관련 예제 GitHub
PPT 강의 자료
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
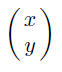
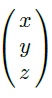
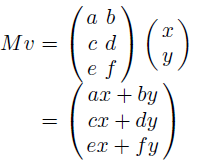
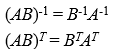
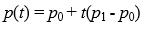
Leave a comment