[Computer Graphics] #9. 라이팅
👻 라이팅
라이팅(Lighting 혹은 Illumination)은 빛과 물체 간 상호작용을 처리하는 기술이며 물리학의 고전적인 주제를 다룬다. 실시간 그래픽스에 적용할 모델 중 가장 간단한 라이팅 모델은 퐁 모델(Phong Model)이다. 70년대 초반에 만들어져서 변형은 되지만 지금까지 쓰이고 있는 모델이다.
👻 퐁 모델
퐁 모델은 크게 네 가지 항으로 나눠진다.
- 디퓨즈 항(Diffuse)
- 스페큘러 항(Specular)
- 앰비언트 항(Ambient)
- 발산광(Emissive)
라이팅을 위해서는 우선 광원(Light Source)을 정의해야 한다. 다양한 광원이 존재하지만 퐁 모델에서는 방향성 광원(Directional Light Source)를 이용하여 정의하고 있다. 이 광원은 광원의 색상과 단일한 입사 방향만 고려하면 되기 때문에 다른 광원에 비해 계산이 쉬운 이유가 크다. 빛이 세고 물체와 멀리 떨어져있다는 가정을 하게 되는데, 쉽게 말해 태양과 같은 광원이라고 볼 수 있다.
앞서 간단하게 보았던 네 개의 항 중, 디퓨즈와 스페큘러 항은 광원으로부터 물체 표면에 직접 들어오는 빛 즉 직접 조명을 다루며, 앰비언트 항은 다른 물체가 반사하는 빛 즉 간접 조명을 다룬다. 발산광은 물체 스스로 빛을 발산하는 경우에 사용된다.
🌱 디퓨즈 항 - 난반사
디퓨즈 항은 난반사(亂反射)로 정의할 수 있다. 난반사는 입사한 빛에 한해 모든 방향으로 반사된다는 특징을 가진다. 어떠한 색을 본다는 것은 그 물체에 반사된 빛을 보는 것으로, 난반사를 이용하면 물체에 대한 색상은 어디에서나 봐도 동일할 것이다. 이러한 표면을 디퓨즈 표면 혹은 램버시안 표면(Lambertian Surface)이라고 한다.
물체 표면으로 들어오는 빛의 방향은 이른바 빛 벡터(Light Vector)에 의해 정의된다. 방향성 광원을 사용한다면 라이팅을 수행할 장면의 모든 지점은 동일한 빛 벡터를 가지게 되는데, 이를 l로 표기한다. 계산상 편의를 위해 방향은 반대로 정의되어 있다.
한편, 물체 표면의 점 p의 노멀 n과 빛 벡터 l 사이의 각도 θ를 입사각(Incident Angle)이라고 하는데, θ가 작을수록 p는 더 많은 빛을 받는다. n과 l이 정규화되어 단위 벡터로 표현되어 있다면, 둘의 내적을 사용하여 p에 들어오는 빛의 양을 결정할 수 있다.
n·l = ||n||||l||cosθ = cosθ
두 벡터의 각도가 90도를 넘어간다는 의미는 빛 벡터가 보이지 않는 곳에 표면이 존재한다는 뜻이다. 하지만 빛의 양이 음수가 되면 안 되므로 다음과 같이 최소값을 정의한다.
max(n·l, 0)
이 값은 p에 들어오는 빛의 강도만을 결정한다.
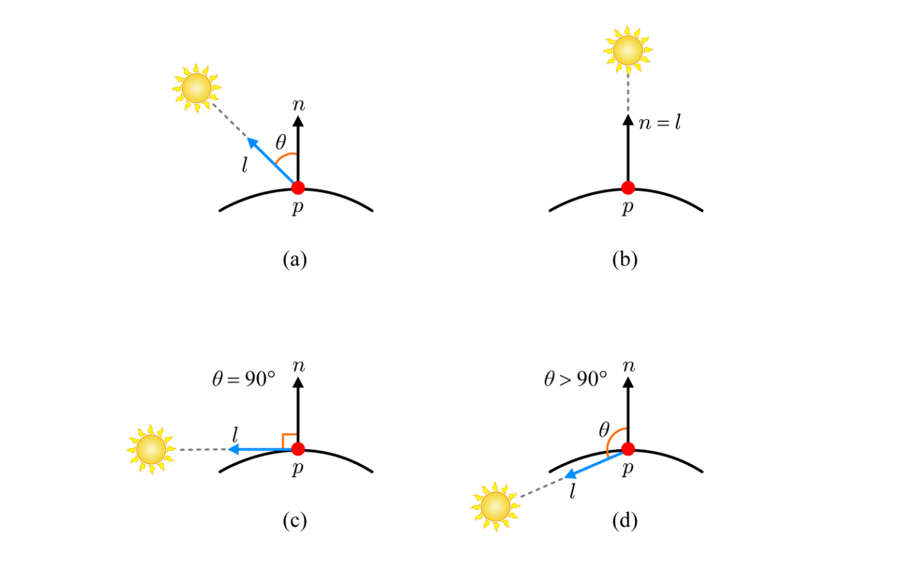
입사각이 90도거나 그 이상일 때 빛을 전혀 받지 못하며 값은 0이 될 것이다. 반대로 입사각이 0도라는 말은 빛 벡터와 표면의 노멀이 일치한다는 의미이며 값은 1, 이 때 받는 빛의 양은 최대가 될 것이다.
물체에 반사되는 빛의 색상은 다음과 같이 정의된다.
sd ⊗ md
여기에서 sd는 광원의 RGB 색상을, md는 물체의 디퓨즈 계수(Diffuse Reflectance)를 나타낸다.
💡 s는 광원(Light Source)을, m은 재질(Material)을 의미하며 해당 기호는 쌍쌍이 곱하라는 의미이다.
앞서 알아보았던 빛의 강도와 합치면 퐁 모델의 디퓨즈 항의 정의가 끝난다.
max(n·l, 0)sd ⊗ md
🌱 스페큘러 항 - 정반사
스페큘러 항은 물체 표면에 하이라이트(Highlight)를 만드는 데 사용된다. 이를 위해서는 시선 벡터(View Vector)와 반사 벡터(Reflection Vector)가 필요하다.
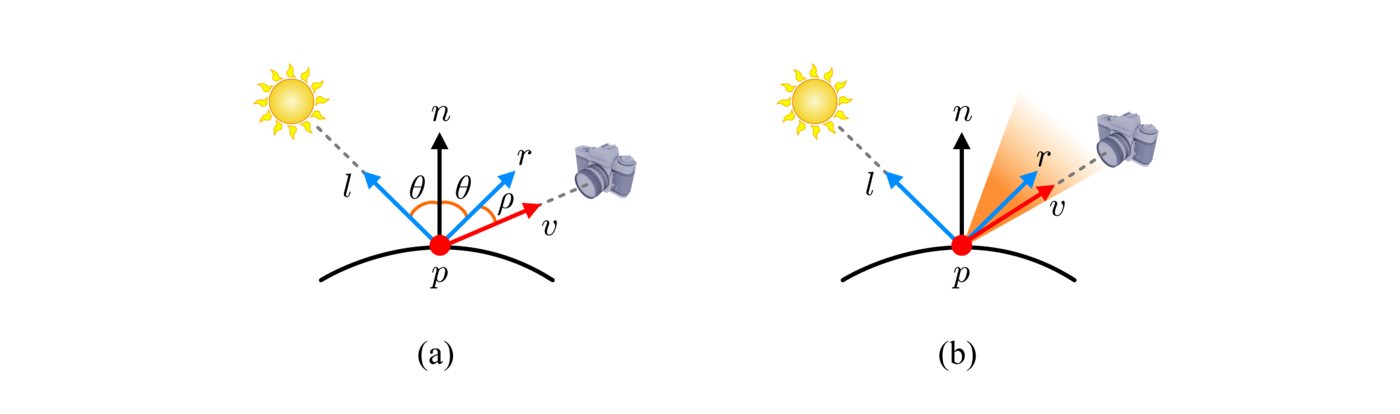
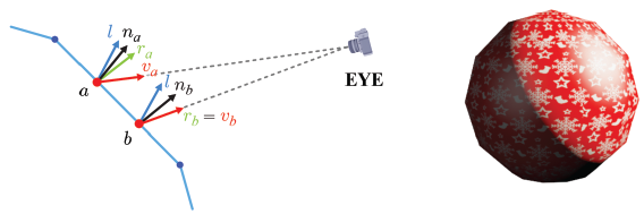
다음은 물체 표면의 점 p, 빛 벡터 l, 그리고 시선 벡터 v와 반사 벡터 r의 관계를 보여준다.
스페큘러 항은 디퓨즈 항과는 반대로 정반사(正反射)를 이용하여 정의한다. 정반사는 입사각과 반사각이 동일하다는 특징을 가진다. 이러한 특징을 이용하면 반사 벡터는 아래와 같이 정의된다.
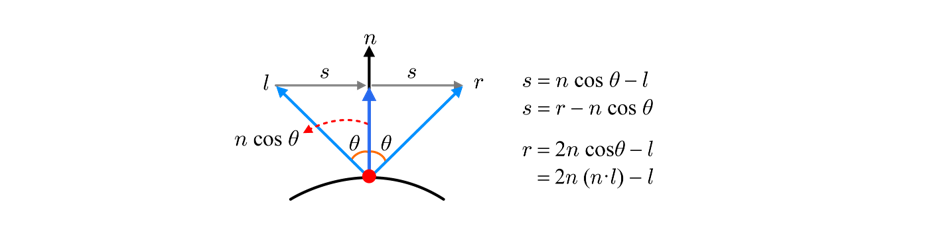
빛 벡터 l과 반사 벡터 r이 공유하는 노멀 벡터가 ncosθ일 때, s를 이용해 r을 구할 수 있다.
💡 모든 벡터가 단위 벡터일 때, 노멀 벡터는
cosθ이다. 수직이 되도록 축소확대를 적용하면 공유 변의 길이는ncosθ가 된다. (0 ≤ cosθ ≤ 1)
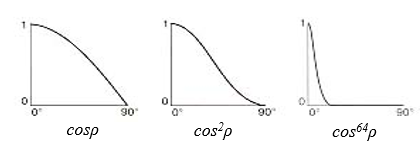
카메라가 어느 위치에 있느냐에 따라 정반사를 볼 수도 있고 못 볼 수도 있다. 즉, 카메라의 위치에 따라 결과값이 급격하게 달라지는, 의존적인 특징을 보여준다. 위의 그림 중 (b) 항을 보면 반사 벡터를 기준으로 주변에 원뿔 모양으로 범위를 가지는 것을 볼 수 있다. 이 부분이 바로 하이라이트를 볼 수 있는 영역이다. 반사 벡터와 시선 벡터 사이의 각도를 ρ라고 할 때, ρ가 작아질수록 하이라이트를 볼 수 있는 영역이 많아지지만, 반대로 커진다면 하이라이트를 볼 수 있는 영역이 좁아지게 될 것이다. 원뿔 속에서 하이라이트가 감소되는 정도는 다음과 같이 근사적으로 계산된다.
(r·v)sh
여기에서 sh는 shininess의 앞 글자로 표면의 매끈함의 정도를 나타낸다. r과 v가 같으면 sh값에 관계없이 1이 되고 최대의 하이라이트가 카메라에 보이게 될 것이다. sh가 커질수록 더 매끈한 표면을 나타낼 수 있게 된다.
💡 만약, 지수값으로 sh가 들어가는 게 아니라면 cosρ의 결과값은 완만하게 감소할 것이다. 이렇게 된다면 정반사가 보이지 않아야 할 부분에서도 보이게 되며 색을 제대로 나타낼 수 없을 것이다.
역시나 음수가 나오는 것을 막기 위해 max 함수를 사용하여 스페큘러 항을 정의하면 다음과 같다.
(max(r·v, 0))shss ⊗ ms
여기에서 ss는 광원의 색상이고, ms는 물체의 스페큘러 계수(Specular Reflectance)이다. 일반적으로 ss와 sd는 동일한 값을 가지지만 ms는 회색조(Gray-Scale)로 표현된다. 물체 고유의 색은 죽이고 원래 라이트 소스의 색만 내보내줘 하이라이트 정보만 보여줘야하기 때문이다.
🌱 앰비언트 항
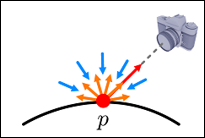
앰비언트 항은 광원이 어디있는지 특정할 순 없지만 어디선가 들어오는, 마치 불을 끄고 시간이 좀 지나면 보이는 것 같은 느낌을 주는 부분이라고 볼 수 있다. 배경광반사라고도 하는데, 반사된 빛들이 어떤 특정한 방향이 아닌 모든 방향을 따라 p점에 들어오게 된다. 이렇게 공간 내 다양한 물체로부터 반사된 빛을 앰비언트 빛(Ambient Light)이라 부르며, 앰비언트 빛의 양은 p의 노멀에 무관하고, p에서 반사되는 빛의 양은 카메라 시선에 무관하다. 방향에 무관하기 때문에 앰비언트 항에 의해서만 렌더링되었다면 해당 물체는 2차원처럼 보일 것이다.
앰비언트 항은 다음과 같이 간단하게 정의된다.
sa ⊗ ma
여기에서 sa는 앰비언트 빛의 RGB 색상이고, ma는 앰비언트 계수(Ambient Reflectance)이다.
🌱 발산광
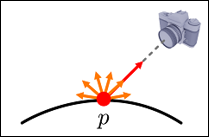
발산광 항은 물체 자신이 빛을 발산하는 경우에 사용된다. 이 RGB 색상은 me로 표기된다. 앰비언트 항과 마찬가지로 결과는 2차원처럼 보인다.
한편, 퐁 모델은 발산광을 가진 물체를 광원으로 취급하지 않기 때문에 같은 공간의 다른 물체를 라이팅하는 데에는 기여하지 못한다. 이것은 퐁 모델의 명백한 한계 중 하나이다.
🌱 퐁 모델 정의
이렇게 네 개의 항을 모두 더하여 퐁 모델을 정의하게 된다.
max(n·l, 0)sd ⊗ md + (max(r·v, 0))shss ⊗ ms + sa ⊗ ma + me

👻 퐁 라이팅을 위한 쉐이더
라이팅은 프래그먼트 쉐이더 내에서 수행된다. 방향성 광원(l)은 일정한 각도에서 들어오기 때문에 유니폼으로 입력된다. 이 밖에 노멀 벡터 n, 반사 벡터 r, 시선 벡터 v가 필요하다.
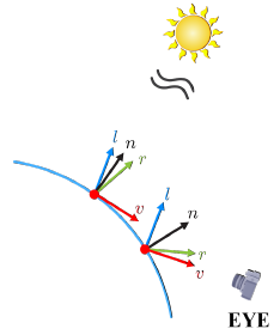
빛 벡터는 유니폼으로 입력받으며 노멀 벡터는 래스터라이저에게서 받는다. 시선 벡터도 정점마다 다르기 때문에 래스터라이저가 전달해줘야한다. 반사 벡터는 노멀 벡터와 빛 벡터가 주어지면 계산이 가능하기 때문에 이 단계에서 자체적으로 계산을 수행하게 된다. 맨 처음 노멀은 오브젝트 공간에서 정의하나 월드 변환을 수행한 후 래스터라이저로 넘겨주게 된다. 빛 벡터도 월드 공간에서 정의되기 때문에 이 밖의 벡터들도 월드 공간 단위여야 한다.
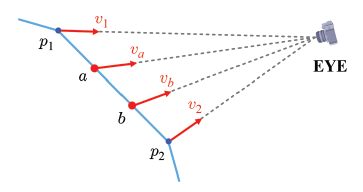
정점 쉐이더에서 빛 벡터, 정점 노멀, 시선 벡터를 전달해주면 래스터라이저가 각 프래그먼트 별로 보간하여 프래그먼트 쉐이더에게 건네주게 된다. 프래그먼트 쉐이더는 각 프래그먼트 별로 라이팅 작업을 수행하게 된다.
🌱 코드 분석
- 퐁 라이팅을 위한 정점 쉐이더 코드
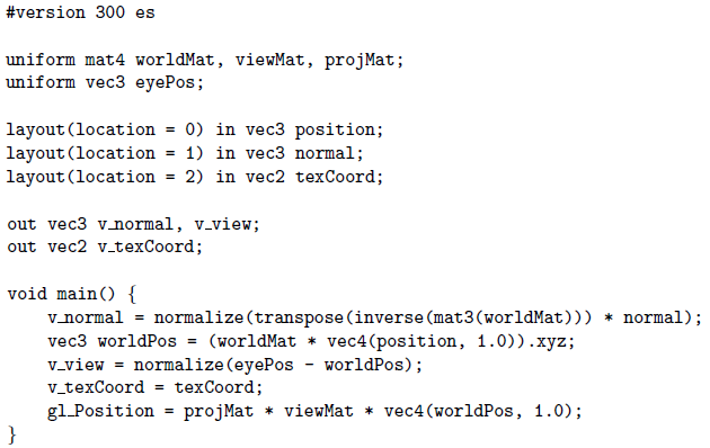
정점 쉐이더(처리) 단계에서 빛 벡터와 시선 벡터를 건네주는 부분이 추가되었다. worldPos가 빛 벡터, eyePos가 시선 벡터이다.
- 퐁 라이팅을 위한 프래그먼트 쉐이더 코드


한 가지 주의해야 할 점은 연산을 수행하기 전 노멀 벡터, 시선 벡터, 빛 벡터를 정규화하는 작업이 있다는 것이다. 정점 쉐이더 단계에서 노멀을 정규화하여 래스터라이저에게 넘겼지만, 래스터라이저가 보간을 수행하면서 노멀이 정규화되어있다는 보장은 없다. 따라서 프래그먼트 쉐이더 단계에서 연산을 수행하기 전 정규화 작업을 한 번 더 진행시켜주어야 한다. 라이팅 연산의 벡터들은 모두 단위 벡터를 기준으로 한다.
➕
퐁 라이팅의 결과값이 1을 넘으면 1로 고정시킨다고 한다. (유니티는 허용한다 했었나..?)
👻 글을 마치며
이번 시간에는 라이팅에 대해 알아보았다. 지난 번 소모임 스터디 때 유니티를 이용해서 모델링 된 나무에 텍스처를 입히고 라이팅을 적용시켜본 적이 있어서 그런지 어떤 식으로 빛을 입혀서 물체의 색상을 정하게 되는지 알게되었다. 처음엔 빛과 색상을 따로 생각했어서 많이 어려웠던 느낌이 큰데 생각해보니 프로그램 내에서 라이팅을 적용하려면 물체의 색상을 변경시키는 방법을 이용하면 되는 것을 깨달았다. 사람들은 천재야.. 그래도 생각보다 어렵지 않아서 재미있게 공부했던 시간이었다.
출처
한정현 컴퓨터 그래픽스 강의 (9장-라이팅)
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment