[Computer Graphics] #11-1. 오일러 변환 및 쿼터니언 연습문제 풀이
👻 연습문제 풀이
11장 오일러 변환 및 쿼터니언 챕터의 연습문제는 총 4개이다.
🌱 1
- 문제
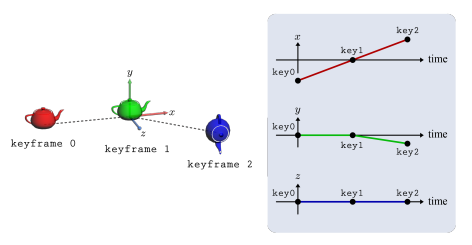
아래 그림은 세 개 키프레임에서 주전자와 위치 그래프를 보여주고 있다. 방향 그래프를 그려라.
- 풀이
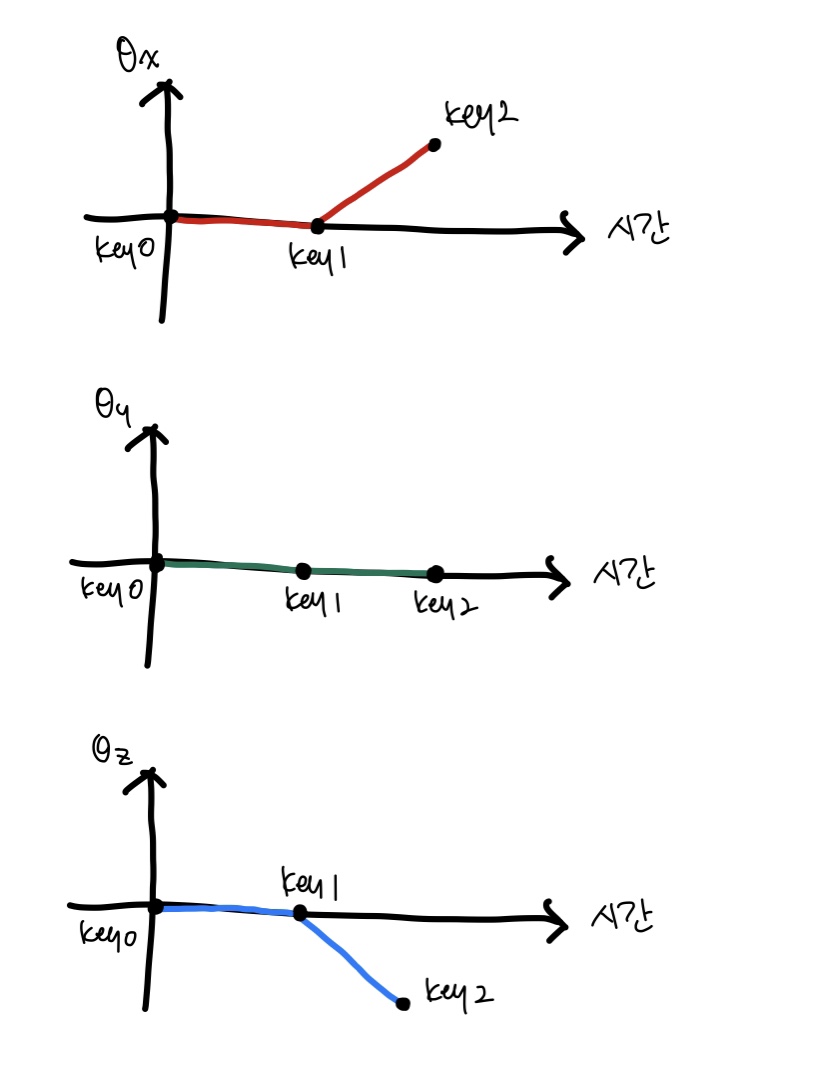
👉 keyframe 0과 keyframe 1 사이는 세 축 모두 회전의 변화가 없다. keyframe 1에서 keyframe 2로 진행되면서 해당 물체는 두 축을 중심으로 회전하게 되었다. 어떤 축을 사용하든 맞는 모습만 되면 중복 정답도 허용이 될 것 같다.
🌱 2
- 문제
오브젝트 공간의 기저를 {u, v, n}으로 표기하자. 물체가 n을 중심으로 θn만큼 회전한 후, 다시 u를 중심으로 θu만큼 회전했다고 하자. 오브젝트 공간 오일러 변환 Ru(θu)Rn(θn)을 월드 공간 회전 행렬의 결합으로 표현하라. 월드 공간의 x, y, z축을 중심으로 하는 회전은 각각 Rx, Ry, Rz로 표기한다.
- 풀이

🌱 3
- 문제
벡터 (0, 1, 0)을 또 다른 벡터 (1, 0, 1) 중심으로 90˚ 회전시키자.
(a) (1, 0, 1) 중심 90˚ 회전을 쿼터니언으로 표현하라. [힌트: 쿼터니언의 허수부는 sine 함수를 가지고 있고, 실수부는 cosine 함수를 가지고 있다.]
(b) 회전 대상인 (0, 1, 0)을 쿼터니언으로 표현하라.
(c) q와 p를 각각 위 (a)와 (b)항의 쿼터니언이라고 할 때, qpq*는 (0, 1, 0)을 (1, 0, 1) 중심으로 90˚ 회전시키는 것을 의미한다. qp와 q*를 계산하라. [힌트: ij = k.]
- 풀이

🌱 4
- 문제
단위 벡터 u를 중심으로 θ만큼의 회전을 표현하는 쿼터니언을 q라 표기하자. q와 -q가 동일한 회전을 표현하는 것을 증명하라.
- 풀이

👻 글을 마치며
이번 시간에는 11장과 관련된 문제를 풀어보았다. 개념은 어려웠는데 그래도 수학 공식이 정해져있고 대입만해서 풀면 되는 문제가 몇 개 있어서 문제는 그리 어렵지 않게 푼 것 같다. 확실히 혼자 공부하면 그냥 넘어갈 수 있었던 부분도 스터디를 통해 다른 관점으로 의문사항을 듣게 되니 신기하고 공부 시야도 확실히 넓어지는 것 같다. 굿! 👍
출처
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment