[Computer Graphics] #11. 오일러 변환 및 쿼터니언
👻 오일러 변환
이전까지는 세 개의 주축을 중심으로 모델을 회전시켜 보았다. 공간에서는 주축과 나란하지 않은 새로운 임의의 회전축을 대상으로 회전을 시킬 수도 있는데, 이는 세 개의 주축을 결합하여 만들게 된다. 이러한 세 개의 주축 중심 회전의 결합을 오일러 변환(Euler Transform)이라 한다. 이 주축은 월드 공간에서 택할 수도 있고, 오브젝트 공간에서 택할 수도 있다.
🌱 월드 공간 오일러 변환
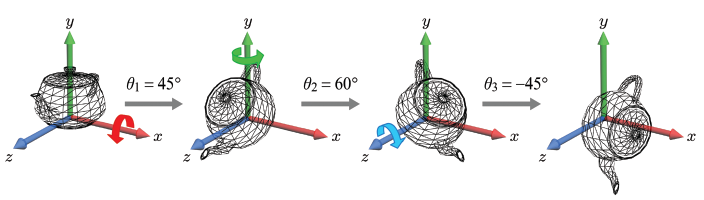
주전자를 월드 공간의 x, y, z축 중심으로 순차적으로 회전시켜 위와 같은 결과를 도출했다고 가정해보자. 여기서, 세 축 중심의 회전각 θ1, θ2, θ3를 오일러 각(Euler Angles)이라 부른다. 세 개의 회전 행렬을 하나로 결합하면 다음과 같다.
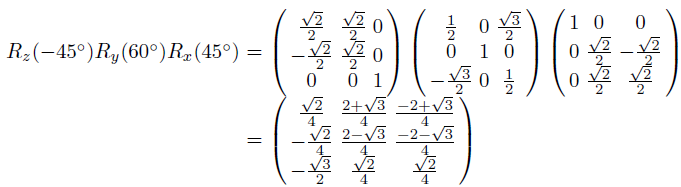
오일러 변환은 반드시 x, y, z축 순서를 따라야 하는 것은 아니다. 아래는 같은 오일러 각을 가지나, 회전의 순서를 달리 결합한 결과이다.
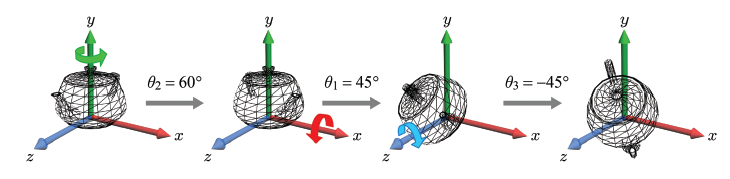
처음 오일러 변환의 결과와 다른 결과가 나오는 것을 확인할 수 있다. 이처럼 오일러 변환의 순서를 바꾸면 결과도 달라진다는 것을 주의해야한다.
🌱 오브젝트 공간 오일러 변환
월드 공간에서 적용했던 오일러 변환을 오브젝트 공간으로 가져와 적용해본다고 생각해보자. 오브젝트 공간의 주축은 모델이 회전하면서 같이 바뀌게 되므로 같은 결과를 기대할 수 없다.
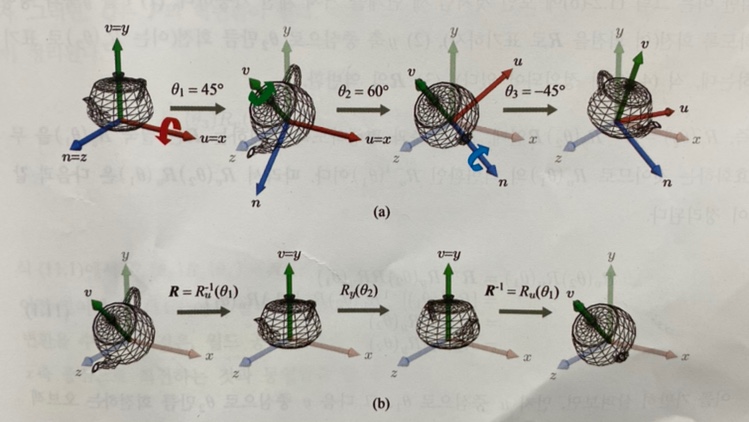
초기에 오브젝트 공간은 월드 공간과 일치하므로, Ru(θ1)은 Rx(θ1)과 같다. 두 번째 회전 Rv(θ2)부터는 다음과 같은 과정이 추가적으로 필요할 것이다.
- v를 y축과 평행하도록 회전(이 회전을 R로 표기)
- y축 중심으로 θ2만큼 회전(이는 Ry(θ2)로 표기)
- R의 역변환
즉, Rv(θ2) = R-1Ry(θ2)R인데, v를 y축과 평행하도록 회전하는 R은 결국 Ru(θ1)을 무효화하는 것이므로 Ru(θ1)의 역변환인 Ru-1(θ1)이다. 따라서 Rv(θ2)Ru(θ1)은 다음과 같이 정리된다.
Rv(θ2)Ru(θ1) = R-1Ry(θ2)RRu(θ1)
= [Ru-1]-1Ry(θ2)Ru-1(θ1)Ru(θ1)
= Ru(θ1)Ry(θ2)
= Rx(θ1)Ry(θ2)
이 식에서, 오브젝트 공간 오일러 변환은 월드 공간 주축을 대신 사용하되 그 순서를 거꾸로 하여 회전하는 것과 동일함을 알 수 있다. 이를 세 개의 축에 적용하여 위 식을 P, n을 z축으로 평행하도록 회전하는 것을 Q로 표기할 때, 오브젝트 공간에서의 오일러 변환은 다음과 같이 정리된다.
Rn(θ3)Rv(θ2)Ru(θ1) = Q-1Rz(θ3)QP
= [P-1]-1Rz(θ3)P-1P
= PRz(θ3)
= Rv(θ2)Ru(θ1)Rz(θ3)
= Rx(θ1)Ry(θ2)Rz(θ3)
앞서 본 것은 세 개의 주축의 회전의 결합을 통해 만들어 낸 변환이다. 물체에 임의의 방향을 제공하는 보다 직접적인 방법은 임의의 축을 중심으로 회전 시키는 것이다. (이건 쿼터니언에서 정리할 것이다.)
👻 키프레임 애니메이션과 오일러 변환
예전 애니메이션에서 유래한 키프레임 애니메이션 기법은, 해당 프레임 전체를 그리는 것이 아닌 훨씬 적은 프레임에 대해서만 동작을 정의하고 나머지 프레임들은 런타임 때 자동으로 채워지도록 해준다. 이를 키프레임 애니메이션이라 하며 직접 동작을 정의하는 프레임들을 키프레임(Key Frame), 중간에 자동으로 채워지는 프레임들을 중간 프레임(In-Between Frame)이라 부른다.
🌱 2차원 키프레임 애니메이션
키프레임에 할당된 중요 데이터를 키 데이터(Key Data)라 부른다. 중간 프레임에서는 이러한 키 데이터가 보간되는데, 시간에 따라 변하는 데이터는 모두 보간 대상이 된다. 대표적인 예로 물치의 위치, 방향, 축소확대 인자 등을 들 수 있다.
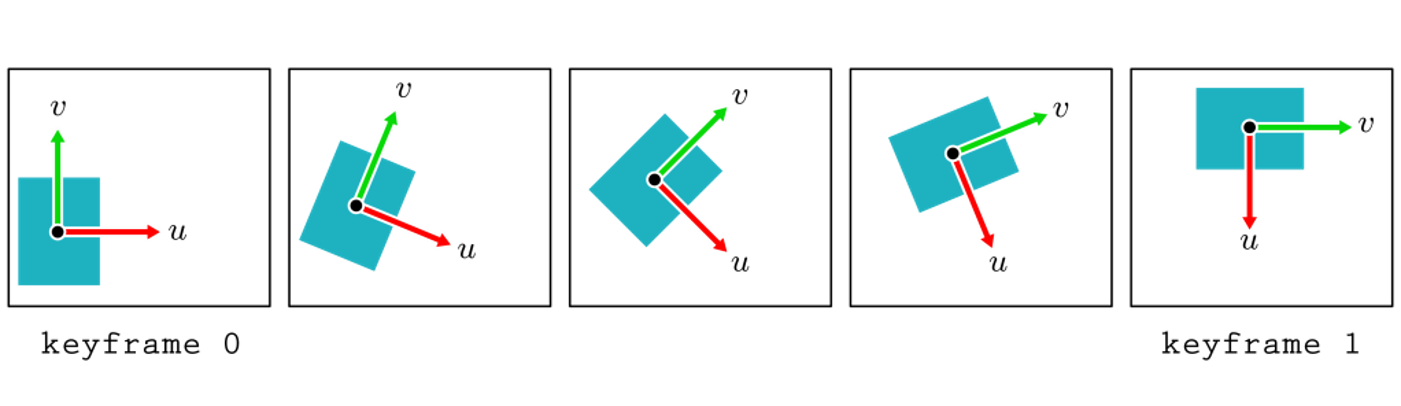
위와 같이 2차원 사각형 애니메이션이 있다고 가정할 때, keyframe 0과 keyframe 1만 직접 동작을 정의해주고 중간 값들은 자동으로 보간이 된 결과를 보여준다. 여기서 사용된 보간법은 앞에서 보았던 선형 보간법이다.
p(t) = (1 - t)p0 + tp1
사각형의 방향도 같은 방식으로 선형 보간된다.
θ(t) = (1 - t)θ0 + tθ1
🌱 3차원 키프레임 애니메이션
2차원 키프레임에서 설명한 개념은 3차원에 그대로 적용된다.
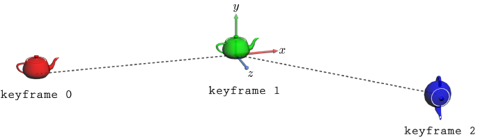

위와 같이 주전자가 시간에 따라 위치와 방향이 변한다고 가정했을 때, 키프레임 중간에 속한 중간 프레임의 값들은 아래의 그래프를 모두 샘플링하여 정의된다.
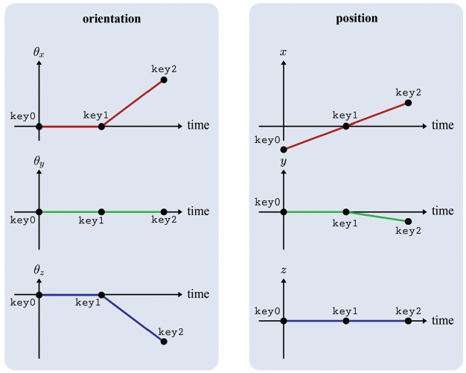
중간 프레임에서의 오일러 각과 x, y, z를 얻기 위해선, 키프레임 별 그래프를 동일한 시간에서 모두 샘플링해야 한다.

반드시 선형 보간법을 이용하여 보간하는 것은 아니다. 부드러운 애니메이션은 종종 고차원 보간을 통해 얻어지며, 위의 예시는 고차원 보간법을 적용한 결과이다. 보간 곡선의 모양을 변경할 수도 있다.
🌱 오일러 각의 보간
오일러 각이 가진 문제 중 하나는, 올바르게 보간된다는 보장이 없다는 사실이다.
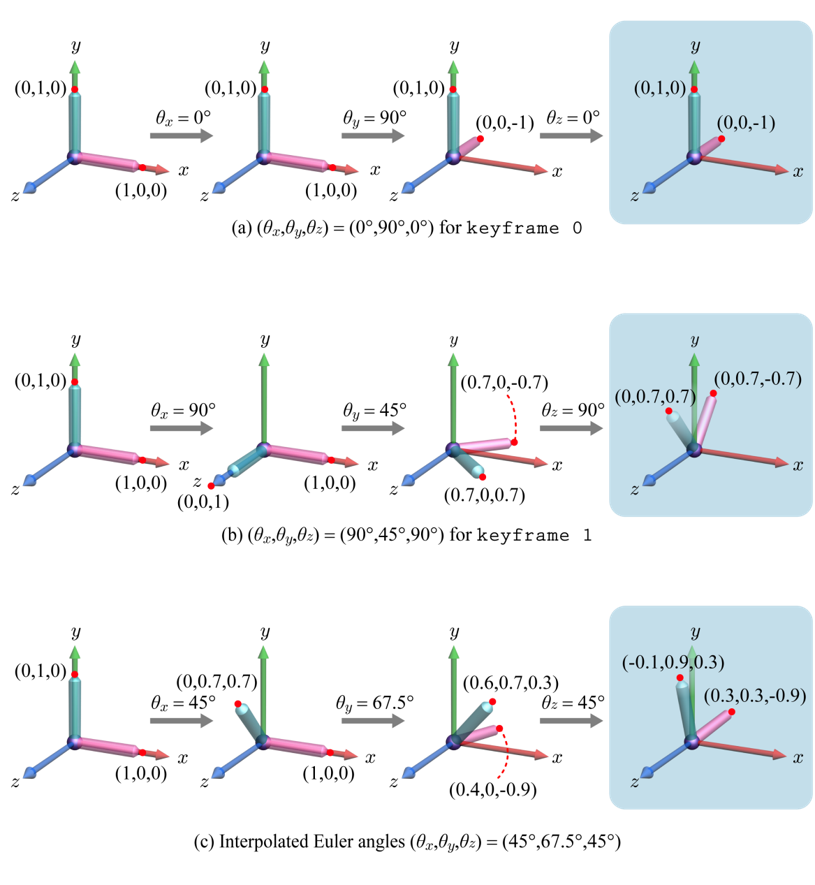
위와 같은 L자형 물체의 키 데이터를 이용해 보간을 한다고 가정하자. (a)항은 keyframe 0, (b)항은 keyframe 1, 그리고 (c)항은 해당 프레임 사이 보간된 중간 프레임의 값을 나타낸다.
해당 보간을 통해 정의된 애니메이션은 다음과 같이 예상할 수 있다.
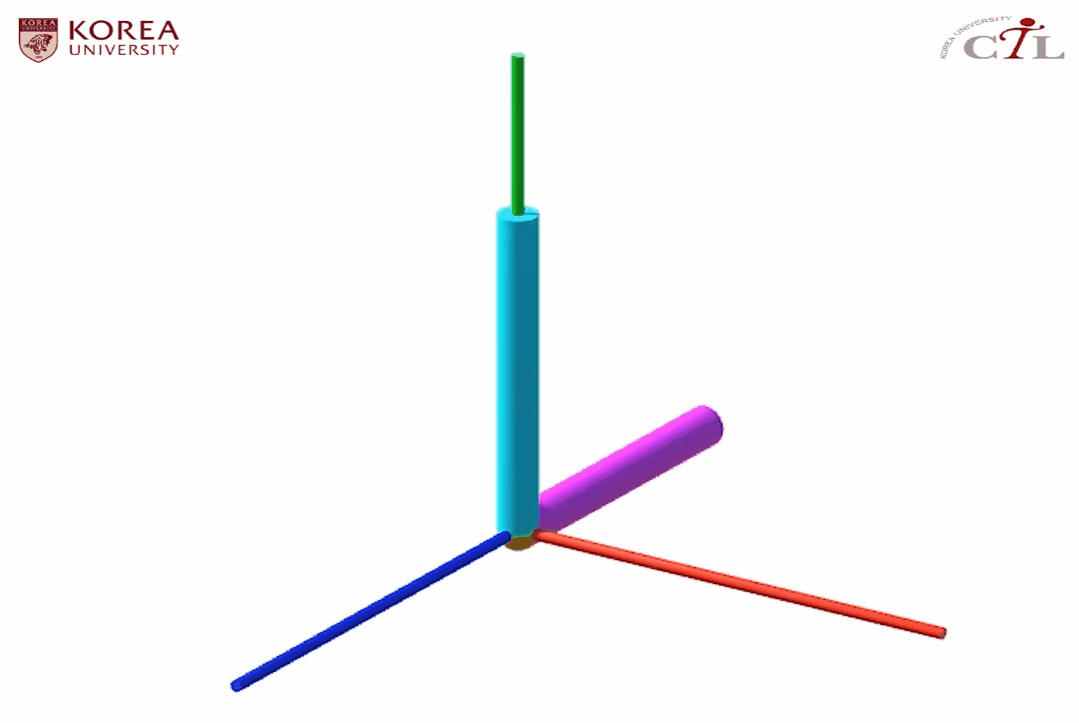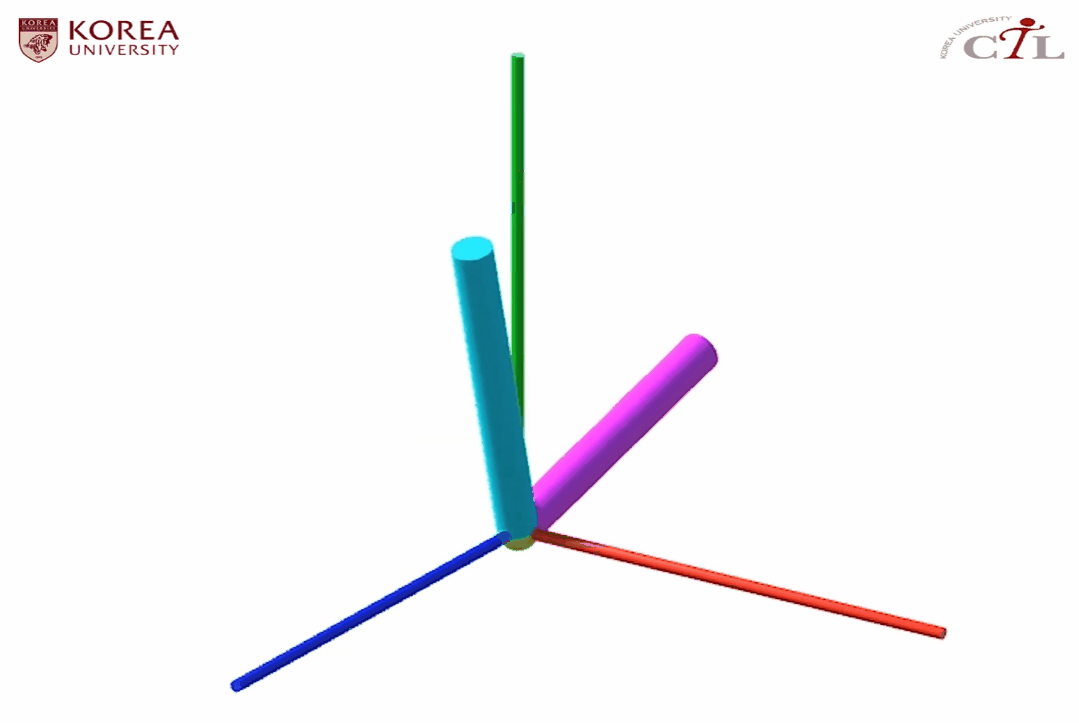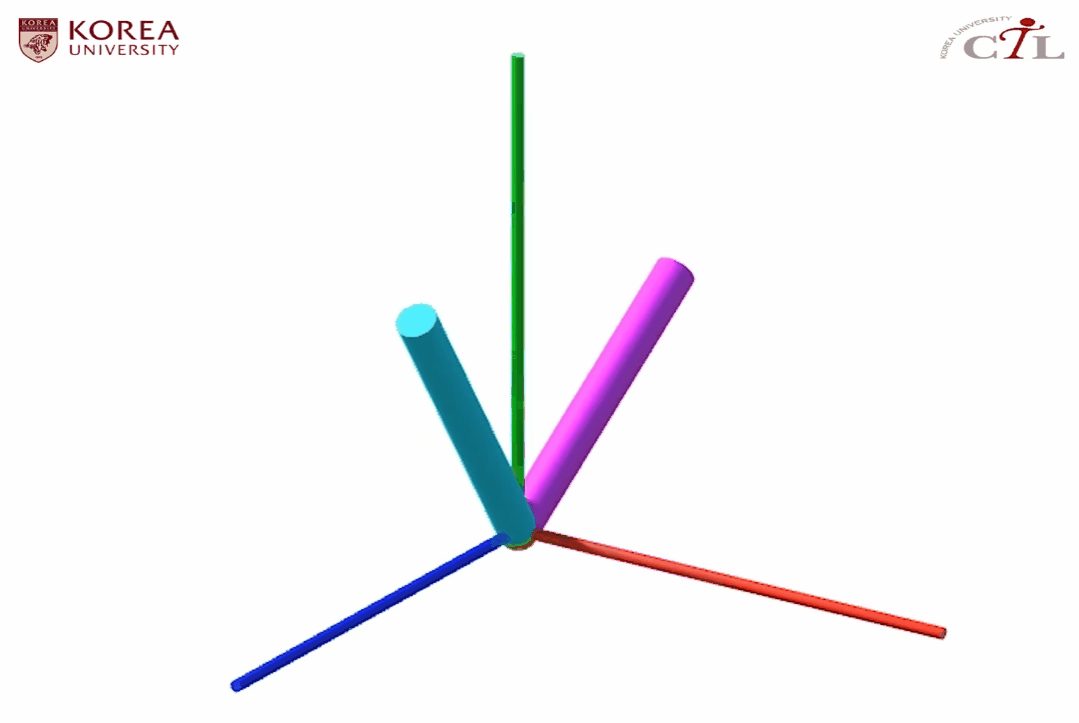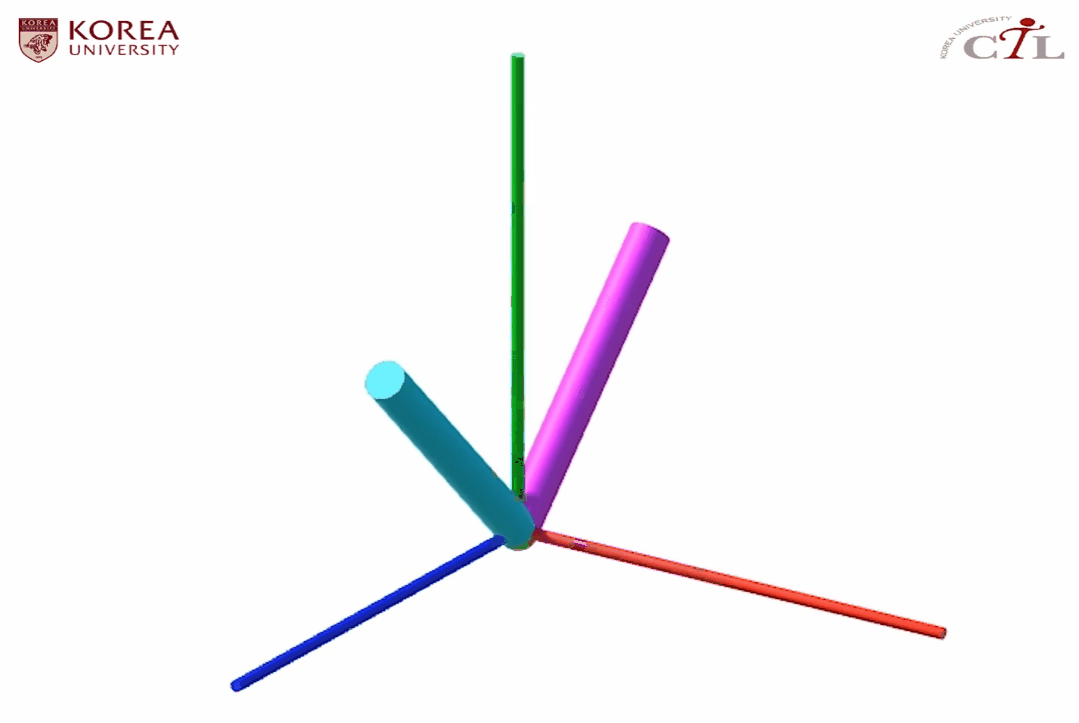
원래대로라면 L자형 물체는 yz 평면에 존재하여 x의 값이 변하지 않아야 하는데 (c)항을 보면 L자형 물체의 양 끝점이 각각 -0.1, 0.3으로 변한 것을 확인할 수 있다. 고로 실제 결과물은 다음과 같다.
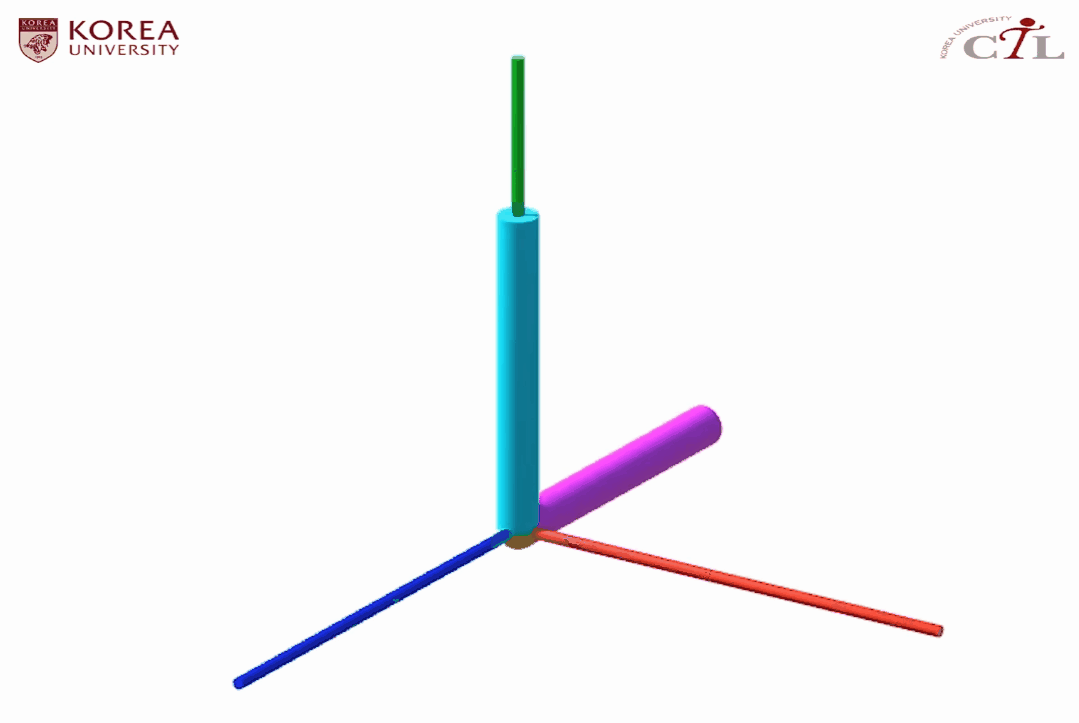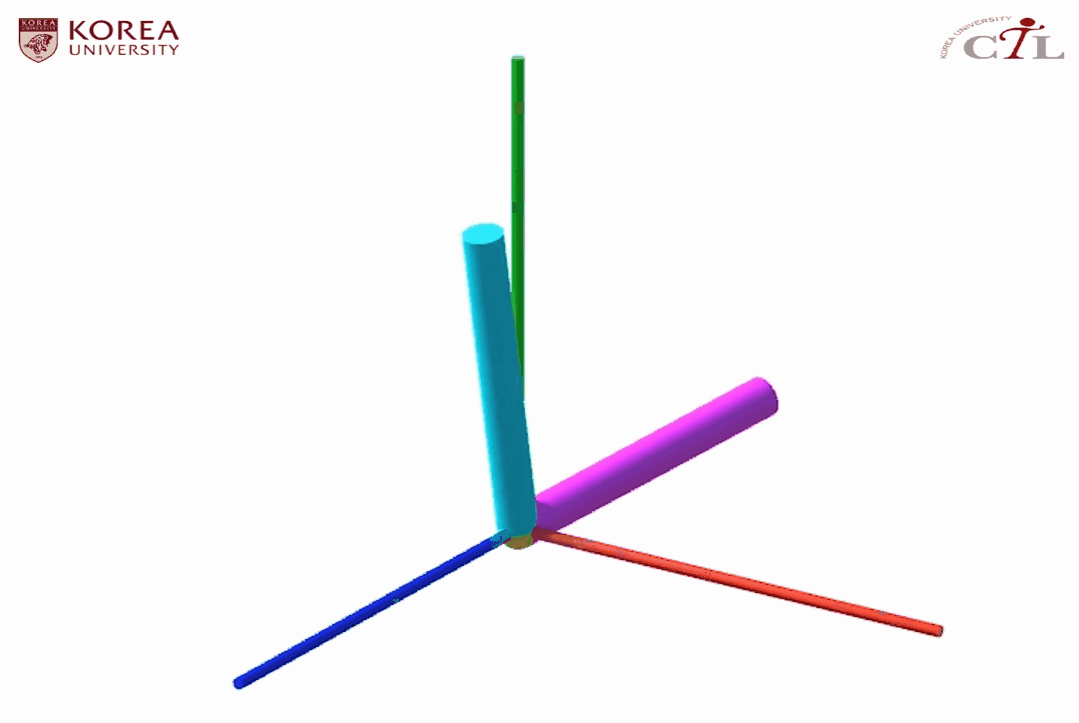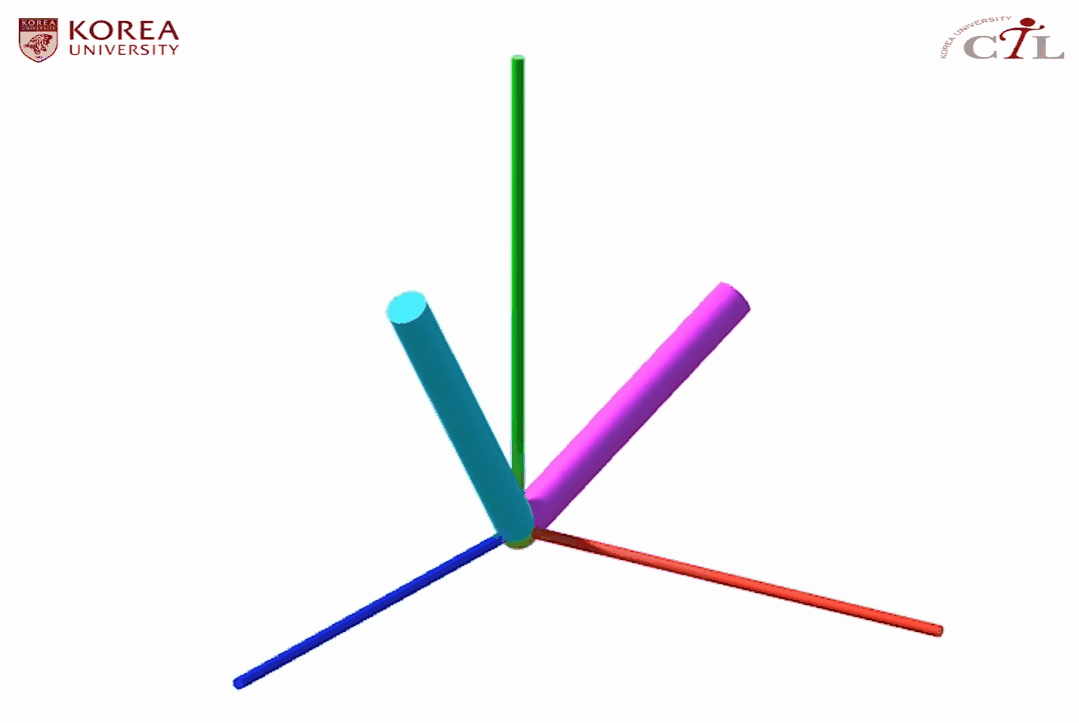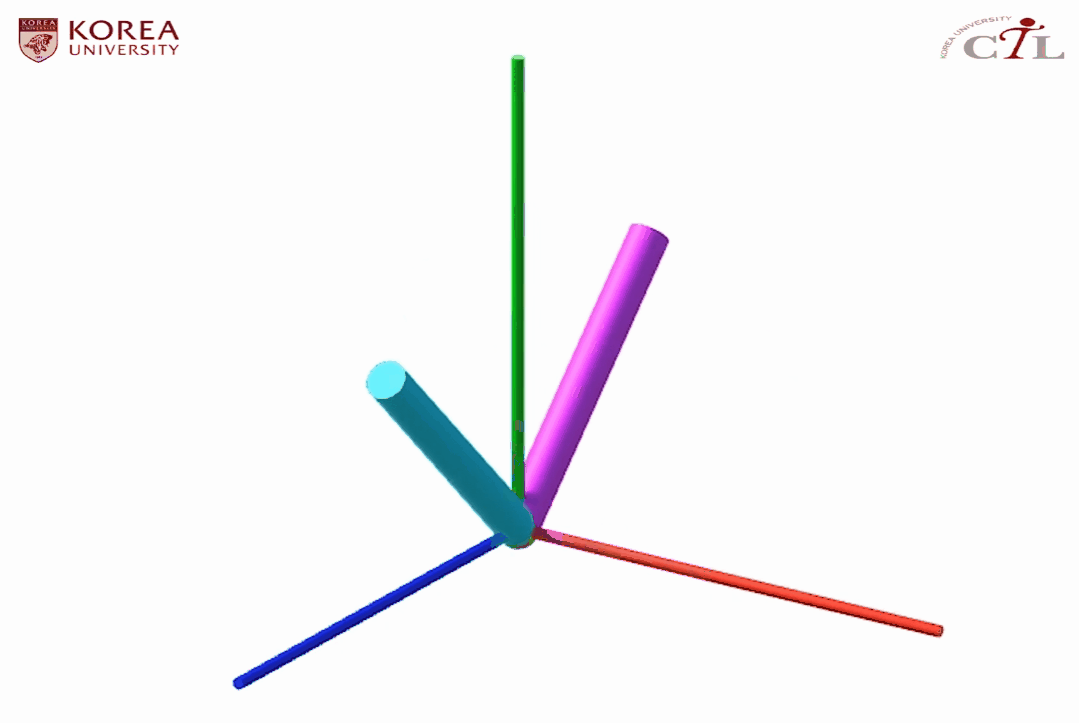
이처럼 오일러 각은 올바르게 보간된다는 보장이 없기 때문에, 보간을 핵심 기능으로 가지는 키프레임 애니메이션에 적합하지 않다.
이러한 문제를 해결하기 위해 나온 개념이 바로 쿼터니언(Quaternions)이다.
👻 쿼터니언
쿼터니언(Quaternions)은 쉽게 말해 복소수의 특성을 이용하여 좌표를 정리한 것이다. q를 약칭으로 사용하며 다음과 같이 네 개의 항으로 표현된다. 이런 특성 때문에 쿼터니언을 4원수로 변역하기도 한다.
(qx, qy, qz, qw) = qxi + qyj + qzk + qw
여기에서 qx, qy, qz는 허수부(Imaginary Part)를 구성하고, qw는 실수부(Real Part)라 하며 i, j, k를 허수단위(Imaginary Unit)이라 한다.
허수단위는 다음과 같은 특징을 가진다.
i2 = j2 = k2 = -1
또한, 두 개의 서로 다른 허수단위가 곱해지면 다음과 같은 순환치환(Cyclic Permutation)적인 특징을 가진다.
ij = k, jk = -k
jk = i, kj = -i
ki = j, ik = -j
두 개의 쿼터니언 (px, py, pz, pw)와 (qx, qy, qz, qw)를 각각 p와 q로 표기할 때, 이들의 곱은 다음과 같이 계산된다.
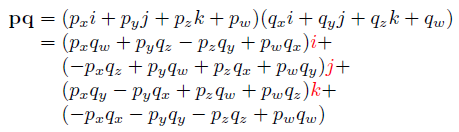
일반 복소수처럼 쿼터니언도 켤레(Conjugate)를 가진다. q의 켤레 쿼터니언은 다음과 같다.
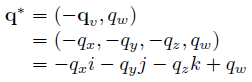
위의 두 식을 이용하면, 두 개의 쿼터니언 p와 q에 대해 (pq)* = q*p*임을 쉽게 증명할 수 있다.
마지막으로, 쿼터니언의 크기는 일반적인 벡터의 경우와 같은 방법으로 계산된다.
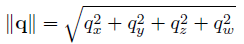
만약 쿼터니언의 크기가 1이라면 해당 쿼터니언은 단위 쿼터니언(Unit Quaternion)이라 불린다.
🌱 쿼터니언을 이용한 회전
2차원 회전 행렬을 이용하여 쿼터니언을 이용한 회전을 정의할 수 있다. x를 실수부로 y를 허수부로 가지는 복소수 x + yi를 p라 표기하고 회전각 θ가 주어졌을 때, 이를 크기가 1인 극형식(Polar Form)의 복소수로 표현하면 cosθ + sinθi가 된다. 이를 q라고 할 때, 이 두 쿼터니언을 곱하면 다음과 같은 결과를 얻는다.
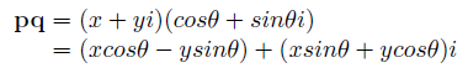
여기서 실수부는 2차원 회전의 x’와 같고 허수부는 y’와 일치함을 발견할 수 있다. 비슷한 방법으로 3차원 회전을 정리해 보자.
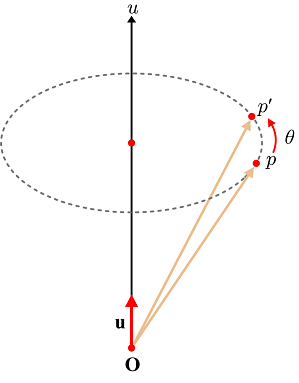
자세한 이미지는 책 189페이지 참고
위 그림에서 회전축은 벡터 u이며 p에서 p’로의 회전을 나타낸다. 여기서 회전을 표현하는 쿼터니언의 크기는 1이 되어야 한다. 이를 위해 u의 단위 벡터 u를 만들면 크기가 1인 극형식의 쿼터니언은 다음과 같이 정의된다.
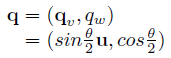
마지막으로 p를 u 중심으로 θ만큼 회전하는 것은 다음과 같이 표현된다.
p’ = qpq*
해당 쿼터니언 연산의 결과도 모두 쿼터니언이다.
🌱 쿼터니언의 보간
회전을 나타내는 두 개의 단위 쿼터니언 p와 q가 있을 때, 이들은 [0, 1] 범위에서 정규화된 파라미터 t를 사용해 다음과 같이 보간된다.
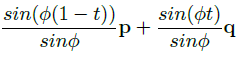
위 식은 선형 보간의 변형으로, 구체 선형보간(Spherical Linear Interpolation; slerp)이라 부른다.
🌱 쿼터니언과 회전 행렬
쿼터니언이 주어졌을 때, 이를 회전 행렬로 전환하면 다음과 같다.
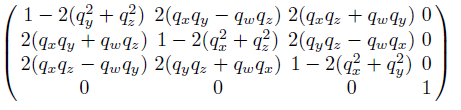
역으로, 회전 행렬이 주어졌을 때 쿼터니언을 계산하는 것 역시 가능하다.
👻 글을 마치며
이번 시간에는 오일러 변환과 쿼터니언에 대해서 알아보았다. 처음 접해보는 개념들이 많아서 이해하는 데 애를 많이 먹었던 챕터였다. 난.. 행렬이 싫어!! 오일러 변환은 쉬웠는데 쿼터니언 개념이 바로 와닿지 않아서 힘들었던 것 같다. 증명도 워낙 많고 뜬금포로 나오는 개념들이 머릿속에서 정리가 되지 않는다 😭😭😭 그래도 큰 틀의 개념만 잡아뒀더니 스터디를 통해 복습을 하면서 자연스레 흡수되는 개념이 몇몇개 존재하는 것 같다. 그래도 복소수는 너무 어렵다!
출처
한정현 컴퓨터 그래픽스 강의 (11장-오일러 변환 및 쿼터니언)
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment