[Computer Graphics] #17-1. 매개변수 곡선과 곡면 연습문제 풀이
👻 연습문제 풀이
17장 매개변수 곡선과 곡면 챕터의 연습문제는 총 9개이다.
🌱 1
- 문제
3차 베지어 곡선의 식은 (1 - t)3p0 + 3t(1 - t)2p1 + 3t2(1 - t)p2 + t3p3이다. 4차 베지어 곡선의 식을 작성하라.
- 풀이

🌱 2
- 문제
3차 베지어 곡선의 식은 (1 - t)3p0 + 3t(1 - t)2p1 + 3t2(1 - t)p2 + t3p3이다. 5차 베지어 곡선의 식을 작성하라.
- 풀이

🌱 3
- 문제
세 개의 2차원 점이 주어졌다: (1, 0), (0, 1), (-1, 0).
(a) 이 점 모두를 지나는 2차 베지어 곡선이 있는데, (0, 1)에서의 매개변수 t는 0.5이다. 이 베지어 곡선의 컨트롤 포인트를 계산하라.
(b) 이 베지어 곡선에서 t = 0.75인 점의 좌표를 계산하라.
- 풀이

🌱 4
- 문제
두 개의 3차 베지어 곡선으로 구성되는 스플라인이 있다. 베지어 곡선의 컨트롤 포인트는 {p0, p1, p2, p3}와 {q0, q1, q2, q3}이며, p3 = q0이다. 두 베지어 곡선이 만나는 점에서 접선 벡터를 공유하도록 만들기 위한 조건을 p2, p3, q0, q1을 이용하여 정의하라.
- 풀이

🌱 5
- 문제
2차 베지어 곡선 p(t)를 따라 이동하는 카메라가 있다. 이 베지어 곡선의 컨트롤 포인트는 {p1, p2, p3}이다. EYE는 곡선 p(t)에 놓이고, AT은 원점과 p4를 연결하는 선분 q(t)를 따라 움직인다. UP은 월드 공간의 y축으로 고정되어 있다.
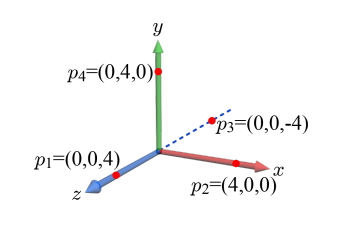
(a) p(t)와 q(t) 모두 [0, 1]의 범위를 가지는 매개변수 t에 의해 정의된다. t = 0.5일 때 p(t)와 q(t)를 계산하라.
(b) t = 0.5일 때 카메라 공간의 기저를 계산하라.
(c) t = 0.5일 때 뷰 변환을 구성하는 이동 및 회전 행렬을 계산하라.
- 풀이

🌱 6
- 문제
어떤 베지어 패치가 아래와 같은 컨트롤 포인트 행렬로 정의되었다. 이 패치의 정의역의 u축은 수평 방향, v축은 수직 방향이다.
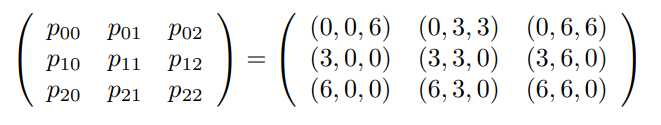
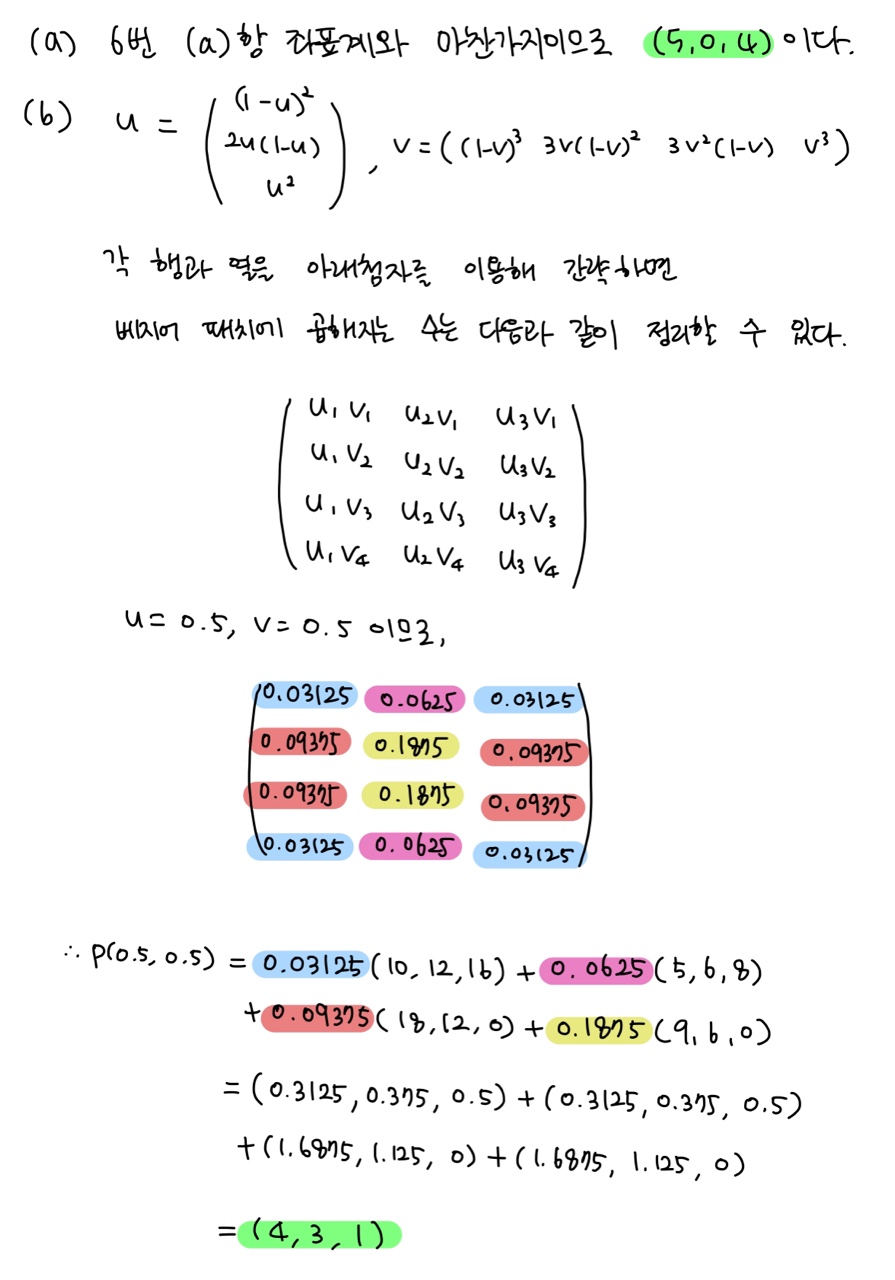
(a) (u, v) = (1, 0)에 해당하는 곡면 위의 점의 좌표는 무엇인가?
(b) 반복적 겹선형 보간을 사용하여 (u, v) = (0.5, 0.5)일 때 곡면 위의 점의 좌표를 계산하라.
- 풀이

🌱 7
- 문제
어떤 베지어 패치가 u 기준으로는 2차, v 기준으로는 3차로 정의되었다. 컨트롤 포인트 행렬은 다음과 같다.
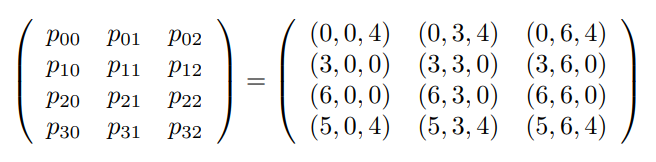
(a) (u, v) = (0, 1)일 때 곡면 위의 점의 좌표를 계산하라.
(b) (u, v) = (0.5, 0.5)일 때 곡면 위의 점의 좌표를 계산하라.
- 풀이
🌱 8
- 문제
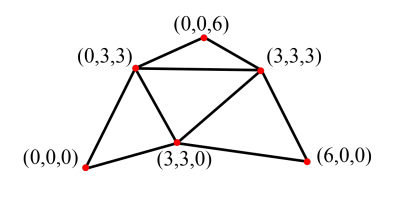
다음과 같은 컨트롤 포인트를 가지는 2차 베지어 삼각형에서, (u, v) = (1/3, 1/3)일 때 곡면 위의 점의 좌표를 계산하라.
- 풀이

🌱 9
- 문제
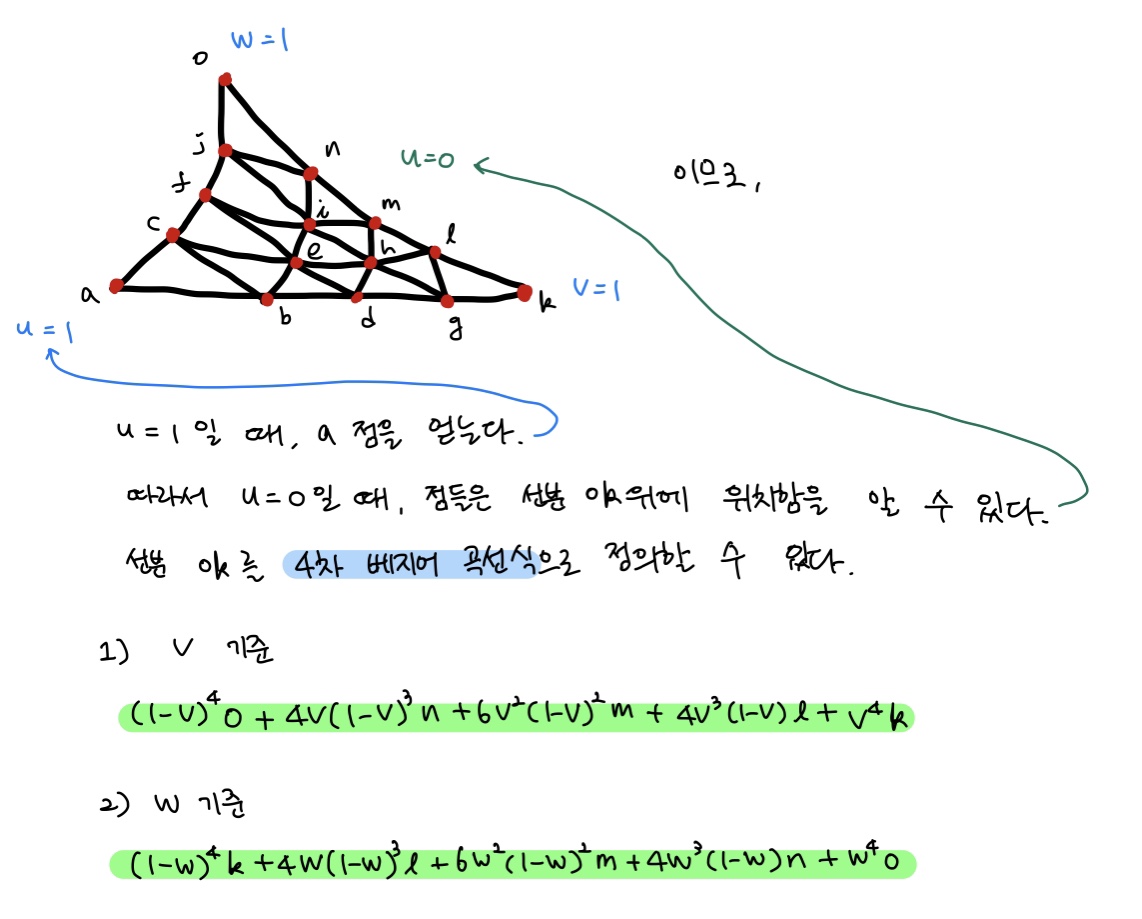
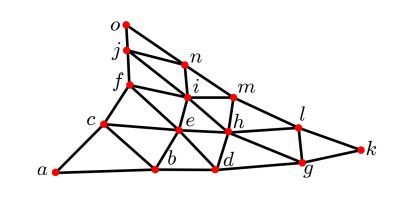
다음과 같은 컨트롤 포인트를 가지는 4차 베지어 삼각형에서, v = 1일 때 k점을 얻고, w = 1일 때 o점을 얻는다. u = 0일 때 얻어지는 곡선의 식을 작성하라.
- 풀이
👻 글을 마치며
이번 시간에는 매개변수 곡선과 곡면에 대한 연습문제를 풀어보았다. 대부분의 계산식은 이제 적응이 돼서^^ 어렵지 않게 풀었다(다만 귀찮았을 뿐)🤗 확실히 연습문제로 개념을 복습하기 때문에 기억에 오래 남는 것 같다. 그리고 그래픽스에서 어떻게 곡면을 정의하는지 알게 되어서 신기하고 재미있는 시간이었다. 이 세상엔 천재가 넘 많아~
출처
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처
관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음
Leave a comment