[Computer Graphics] #17. 매개변수 곡선과 곡면

👻 매개변수 곡선과 곡면

이제까지 3차원 물체를 표현하는데 폴리곤 메시를 사용했다. 폴리곤 메시는 부드러운 곡면을 ‘근사적으로’ 표현한 것이다. 부드러운 곡면을 ‘정확하게’ 표현하기 위해서는 매개변수(Parameter)의 함수를 사용한다. 매개변수 곡면(Parametric Surface)은 CAD/CAM(Computer-Aided Design and Manufacturing)분야에서 오래전부터 사용되었는데, 최근 GPU가 이를 지원하기 시작함에 따라 실시간 그래픽스 분야에서 새롭게 주목을 받게 되었다.

매개변수 곡면을 표현하는 기법은 여러 종류가 있다. 그 중에 가장 간단한 것이 베지어 곡면(Bézier Surface)이며, 베지어 곡면의 기본은 베지어 곡선(Bézier Curve)이다. 이들에 대해 알아보자.

---

👻 매개변수 곡선

매개변수 곡선(Parametric Curve)은 매개변수 t의 함수로 표현된다. 또 다른 매개변수 곡선인 허밋 곡선(Hermite Curve)를 포함하여 알아보자.

---

🌱 베지어 곡선

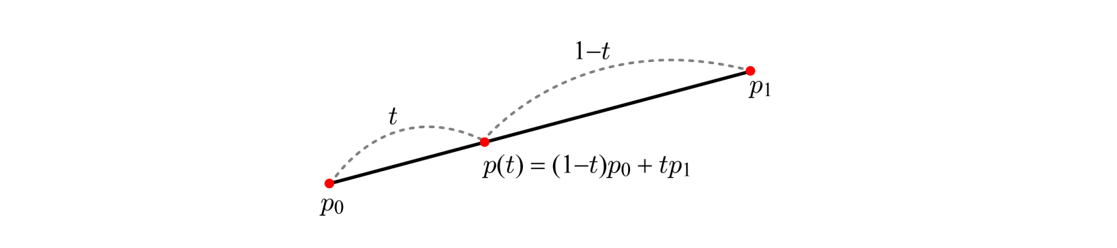
위에서 보여지는 선분은 p₀와 p₁의 선형보간(Linear Interpolation)으로 표현된다. 여기에서 t는 [0, 1] 범위에 있으며 (1 - t)와 t는 각각 p₀와 p₁에 대한 가중치(Weight)이고, p(t)는 이 두 점의 가중치 합(Weighted Sum)이다.

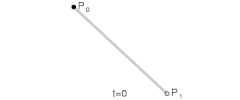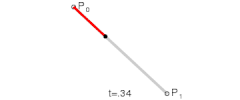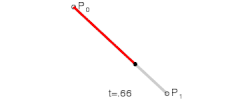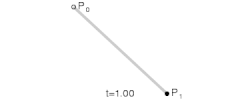
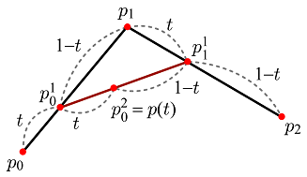
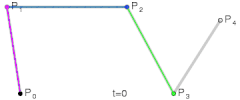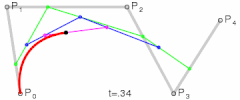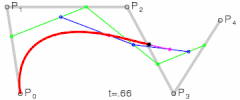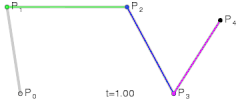
선분은 두 개의 끝점으로 정의되지만, 곡선을 만들기 위해서는 세 개 이상의 점이 필요하다. 세 개 이상의 점에 대해 선형보간을 재귀적(Recursive)으로 반복하면 베지어 곡선을 정의할 수 있는데 이를 드 카스텔조 알고리즘(de Casteljau Algorithm)이라 부른다. 세 개의 점 p₀, p₁, p₂가 주어지면, 일단 p₀와 p₁, 그리고 p₁과 p₂를 선형보간한다.

p₀¹ = (1 - t)p₀ + tp₁
p₁¹ = (1 - t)p₁ + tp₂

위 식에서 위첨자 1은 첫 번째 재귀 단계임을 의미한다. 이를 다시 선형보간하면 다음과 같다.

p₀² = (1 - t)p₀¹ + tp₁¹

앞서 첫 번째 재귀 단계를 거친 식을 두 번째 재귀 단계의 식에 대입하면 t의 2차 함수를 얻게 되는데, 이것이 바로 베지어 곡선이다.

p₀² = p(t) = (1 - t)²p₀ + 2t(1 - t)p₁ + t²p₂

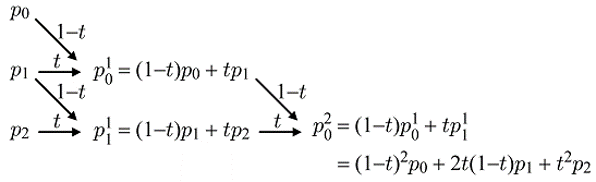
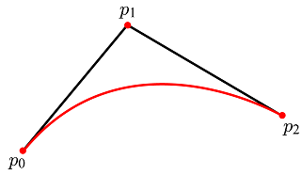
위 이미지에서 보인 것처럼 이 곡선은 p₀에서 시작하여 p₂에서 끝나는데, p₀는 t = 0일 때, p₂는 t = 1일 때에 해당한다. 한편 이 곡선은 p₁ 방향으로 휘지만 이 점을 지나지는 않는다. 이러한 베지어 곡선을 정의하는 p₀, p₁, p₂를 컨트롤 포인트(Control Point)라고 부른다. 2차 베지어 곡선은 최대 1개의 변곡점을 가진다.

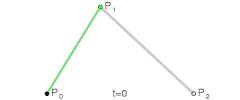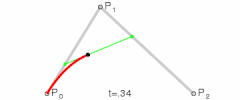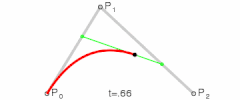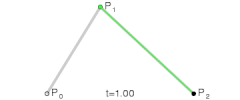
3차 이상의 베지어 곡선도 드 카스텔조 알고리즘으로 정의된다.

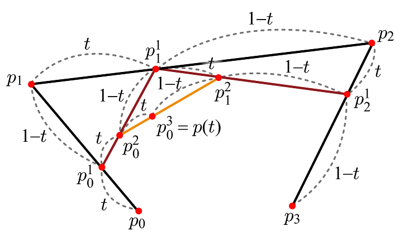
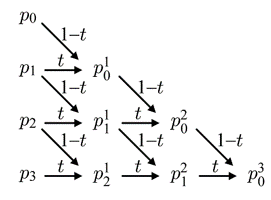
3차 베지어 곡선은 네 개의 컨트롤 포인트에 의해 정의된다. 또한, 3차 베지어 곡선은 최대 2개의 변곡점을 가진다.

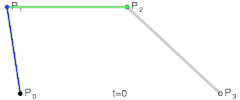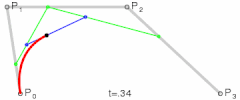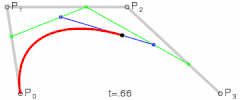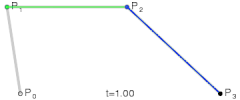
• 3차 베지어 곡선 식
  p(t) = (1 - t)³p₀ + 3t(t - t)²p₁ + 3t²(1 - t)p₂ + t³p₃

2차 및 3차 베지어 곡선을 일반화하면, (n + 1)개의 컨트롤 포인트로 n차 베지어 곡선을 정의할 수 있으며, 각 컨트롤 포인트의 가중치는 매개변수 t의 다항식이다. 이를 번스타인 다항식(Bernstein Polynomials)이라고 부른다. n차 베지어 곡선에서 컨트롤 포인트 p_i에 대한 번스타인 다항식은 아래와 같다.

B_iⁿ(t) = _nC_itⁱ(1 - t)^{n - i}

n차 베지어 곡선 p(t)는 B_iⁿ(t)를 이용하여 다음과 같이 정의된다.

p(t) = ∑ⁿ_i=0B_iⁿ(t)p_i

한편, 4차 이상의 베지어 곡선에서는 종종 예기치 않은 뒤틀린 모양이 만들어지는 등의 문제가 발생하기 때문에 그래픽스 분야에서는 3차 베지어 곡선을 가장 많이 사용한다. 3차 베지어 곡선으로 표현 불가능한 복잡한 곡선은 이러한 3차 베지어 곡선을 여러 개 이어붙이면 된다.

💡 4차 베지어 곡선의 예

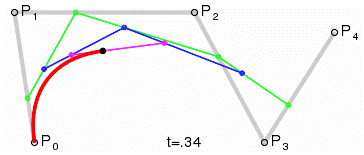
베지어 곡선을 렌더링하기 위해서는 매개변수 t의 값을 조금씩 증가시켜 가면서 이에 해당하는 곡선 상의 점을 계산한 후 이 점들을 선분들로 잇는 방식을 취한다. 이 과정을 테셀레이션(Tessellation)이라 부른다.

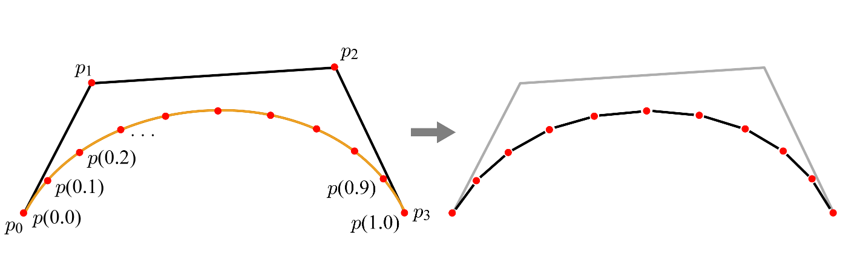
💡 매개변수 t를 균일하지 않게 증가시켜 가면서 테셀레이션을 수행할 수도 있다. 예를 들어, 곡률이 높은 부분은 조밀하게, 곡률이 낮은 부분은 듬성듬성 테셀레이션을 수행할 수 있다.

베지어 곡선이 가지는 특징 중 하나인 아핀 불변성(Affine Invariance)은, 아핀 변환이 이루어져도 점, 직선 및 평면이 그대로 보존됨을 의미한다. 베지어 곡선의 아핀 변환 및 렌더링 과정을 생각해 봤을 때, 이를 구현하는 방법은 두 가지가 있음을 알 수 있다. 첫 번째는 테셀레이션을 먼저 수행하고 그 결과 생성된 점들에 대해 아핀 변환을 적용하는 것, 두 번째는 베지어 곡선의 컨트롤 포인트에 대해 아핀 변환을 먼저 적용한 후, 변환된 컨트롤 포인트를 사용해 테셀레이션을 수행하는 것이다.

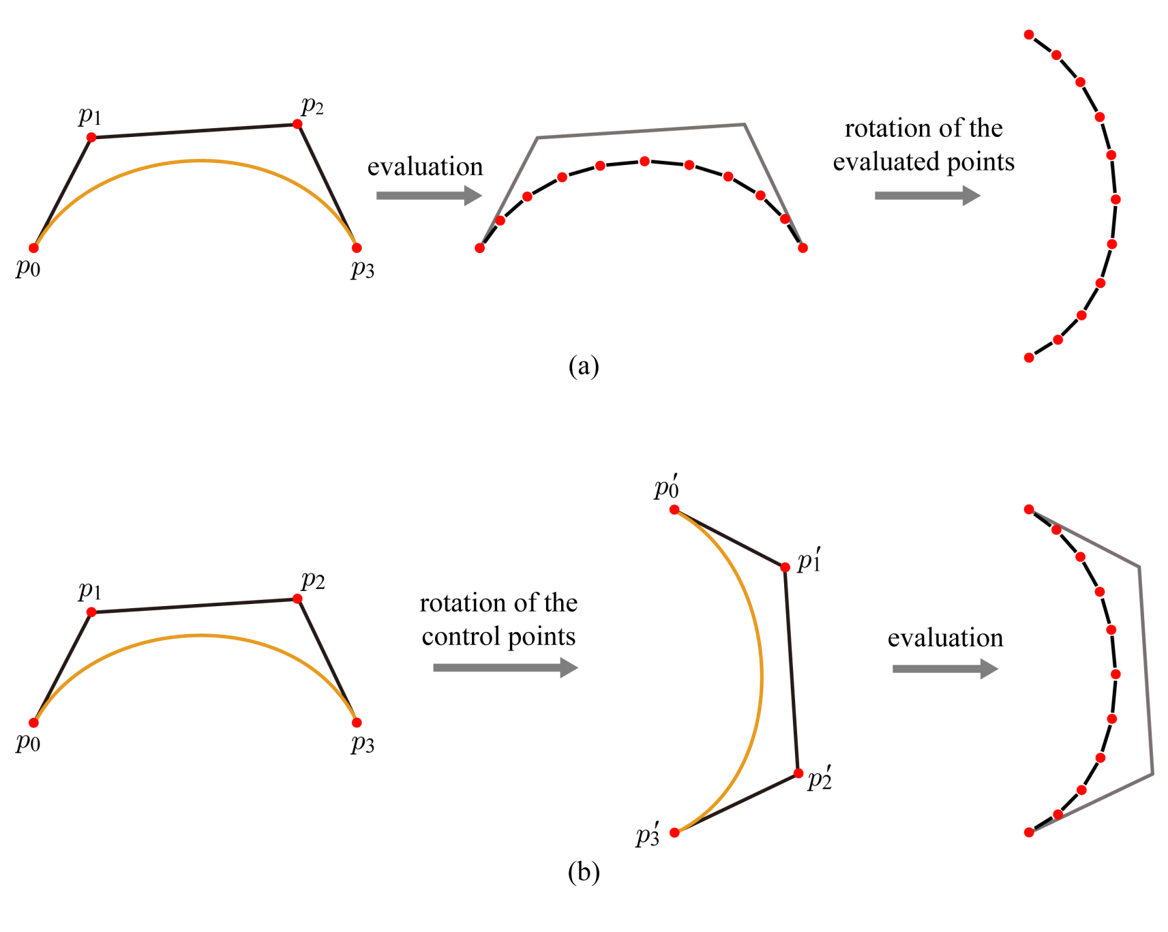
위 이미지에서 그림-(a)는 테셀레이션 수행 후 아핀 변환이 이루어진 결과이고, 그림-(b)는 아핀 변환 후 테셀레이션이 수행된 결과이다. 그 결과는 동일하지만, 보다 적은 수의 점에 대해 아핀 변환을 적용하는 후자가 보다 효율적이다.

---

🌱 허밋 곡선과 캣멀-롬 스플라인

3차 베지어 곡선 함수를 t에 대해 미분하면 다음과 같은 1차 도함수를 얻는다.

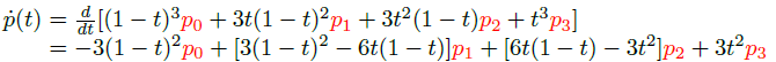
이는 베지어 곡선에 접하는 접선 벡터(Tangent Vector)를 나타낸다. 끝점 p₀와 p₃에서의 접선 벡터를 각각 v₀와 v₃라 할 때, 이는 위 식의 매개변수 t에 0과 1을 대입하여 얻을 수 있다.

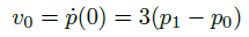
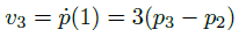
이는 그림으로 나타내면 아래와 같다.

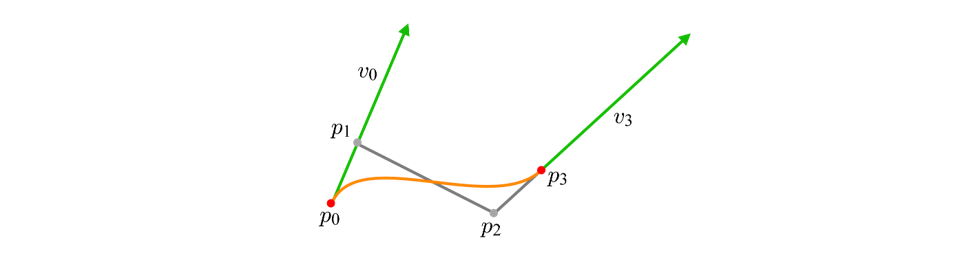
위 식을 다시 쓰면 다음과 같다.

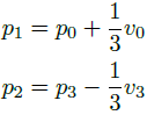
위 두 식을 사용하여 베지어 곡선을 다음과 같이 바꿔 쓸 수 있다.

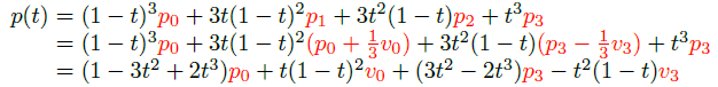
위 식은 두 개의 끝점 p₀와 p₃, 그리고 그 점에서의 접선 벡터 v₀와 v₃를 사용하여 곡선을 정의할 수 있음을 보여준다. 이러한 곡선 표현법을 허밋 곡선(Hermite Curve)이라 부른다. 양 끝점과 그 점의 접선 벡터로 정의된 허밋 곡선은 각 컨트롤 포인트로 정의된 베지어 곡선과 동일한 모양을 가진다.

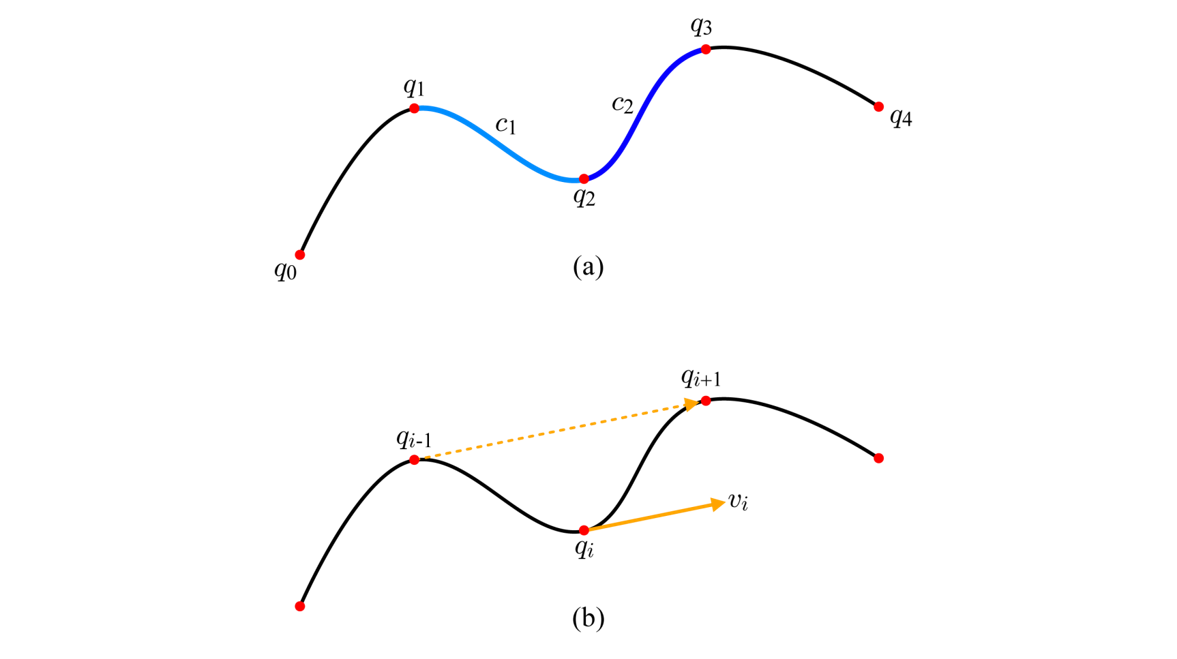
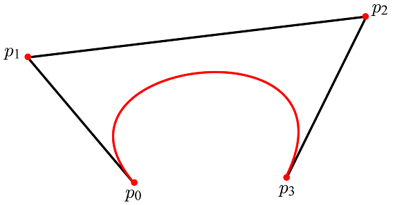
여러 개의 점이 주어졌을 때 이를 모두 지나는 곡선을 만든다고 생각해보자. 위 이미지에서 그림-(a)는 다섯 개의 점 {q₀, q₁, q₂, q₃, q₄}를 지나는 곡선의 예를 보여준다. 이렇게 복잡한 곡선은 인접한 한 쌍의 점 q_i와 q_{i + 1}마다 매개변수 곡선을 정의하고 이들을 부드럽게 이어붙이는 방식으로 만들 수 있다. 이런 방식으로 만들어진 곡선을 스플라인(Spline)이라고 부른다.

반면, 허밋 곡선의 개념에서 생각해보자. 두 허밋 곡선이 만나는 점에서 양쪽의 접선이 같도록 하면, 둘은 부드럽게 이어지고 스플라인 전체도 부드러워진다. 이렇게 두 허밋 곡선이 만나는 점에서 접선 벡터를 공유하며, 이 접선 벡터를 계산하는 여러 가지 방법 중, 캣멀-롬 스플라인(Catmull-Rom Spline)은 q_i에서의 접선 벡터 v_i를 정의하기 위하여 아래 식처럼 q_{i - 1}과 q_{i + 1}을 사용한다.

v_i = τ(q_{i + 1} - q_{i - 1})

여기서 τ(타우)는 q_i의 곡률을 결정하는데, 보통 0.5로 설정된다. 캣멀-롬 스플라인은 게임에서 많이 사용된다.

---

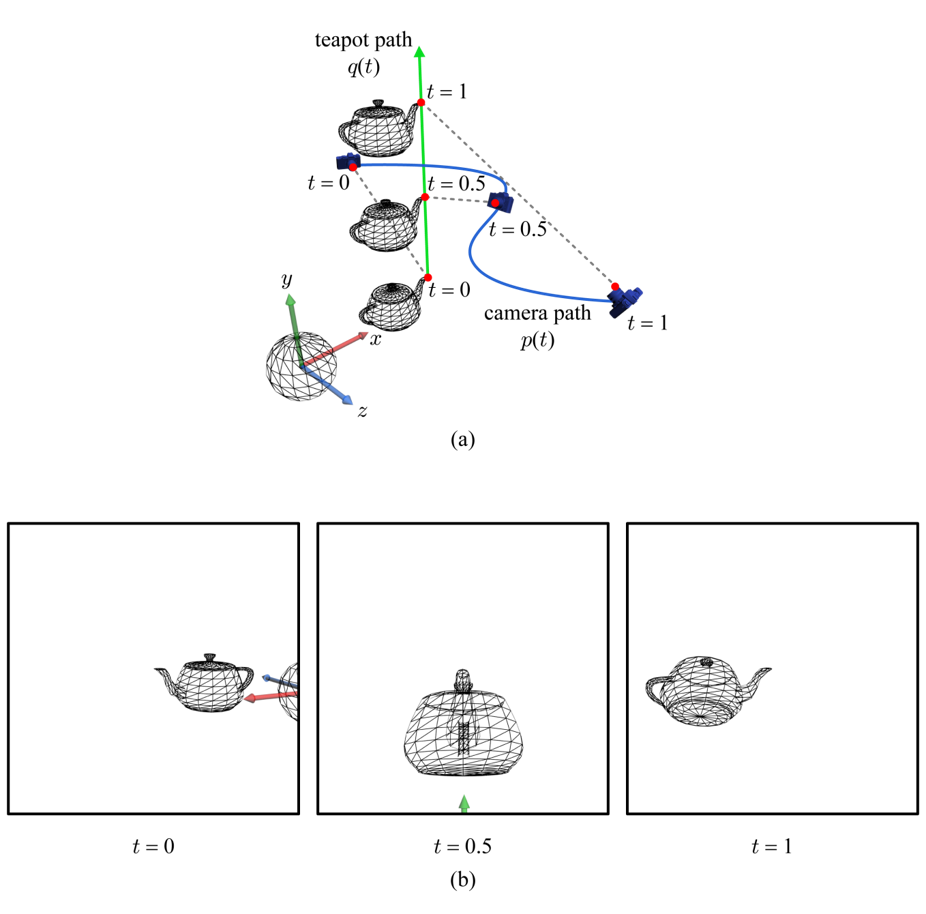
🌱 응용 사례 : 카메라 경로

매개변수 곡선의 용도는 다양하다. 대표적으로 카메라 경로 설정의 경우, 이를 위해 캣멀-롬 스플라인이 종종 사용되는데, 간단한 논의를 위해 카메라 경로는 하나의 허밋 곡선 p(t)로 정의되었다고 가정해보자.

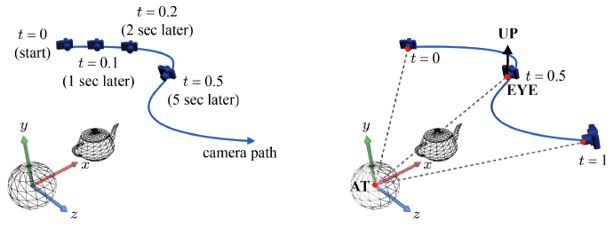
카메라 파라미터 {EYE, AT, UP} 중 EYE는 특정한 t값을 p(t)에 대입하여 얻어낼 수 있는데, t를 지속적으로 증가시키면 곡선 p(t)를 따라 이동하는 EYE를 얻어낼 수 있다.

AT과 UP은 카메라의 방향을 결정한다. 오른쪽 그림에서 AT은 월드 공간의 원점으로 고정되었고, UP은 y축으로 정해졌다. 이렇게 {EYE, AT, UP}이 결정되면 카메라 공간의 기저 {u, v, n}을 계산할 수 있다.

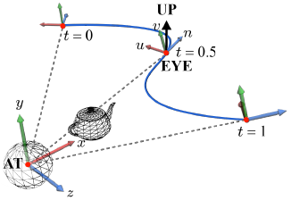
위의 곡선을 따라 카메라가 이동하면서 생긴 결과물은 아래와 같다.

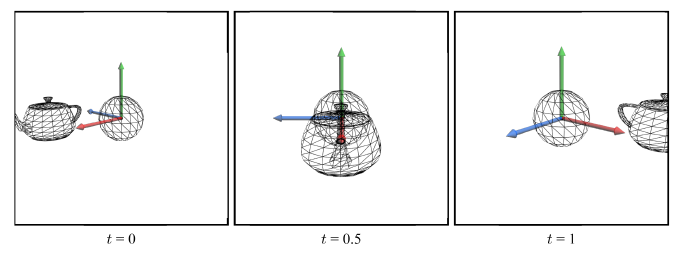
또 다른 예로, 주전자가 위쪽을 향해 이동하고, AT이 주정자 주둥이 끝 위치로 정해졌다고 가정해보자. 이 경우 AT의 움직임은 또 다른 곡선 q(t)로 정의할 수 있다. 즉, 매 프레임마다 EYE와 AT은 각각 p(t)와 q(t)에 특정한 t값을 대입하여 계산된다. UP이 여전히 y축으로 고정되어 있다면 아래와 같은 영상을 얻을 것이다.

---

👻 매개변수 곡면

이제 곡면에 대해 알아보자. 경계를 가진 곡면을 패치(Patch)라 부르는데, 베지어 곡선을 확장하여 베지어 패치를 정의할 수 있다.

---

🌱 겹선형 패치

가장 단순한 형태의 패치는 겹선형 패치(Bilinear Patch)이다.

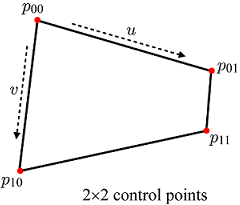
위 이미지는 네 개의 컨트롤 포인트 p₀₀, p₀₁, p₁₀, p₁₁을 사용해 정의된 겹선형 패치이다. 일반적으로 이들 컨트롤 포인트들은 한 평면에 있지 않다.

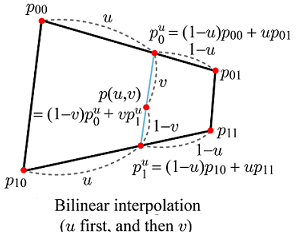
패치를 만들기 위해선 먼저 u 방향으로 컨트롤 포인트를 보간한다. 이를 식으로 나타내면 다음과 같다.

p₀^u = (1 - u)p₀₀ + up₀₁
p₁^u = (1 - u)p₁₀ + up₁₁

이제 이 두 점을 v 방향으로 보간한다.

p(u, v) = (1 - v)p₀^u + vp₁^u
    = (1 - u)(1 - v)p₀₀ + u(1 - v)p₀₁ + (1 - u)p₁₀ + uvp₁₁

앞서 u 방향으로 보간되어 만들어진 두 점을 이은 선분들이 무한히 많이 모여 겹선형 패치를 생성하는 것으로 생각할 수 있다.

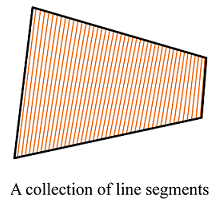
이 그림에서 각각의 선분은 [0, 1] 범위에서 고유한 u값에 의해 지정되고, 선분 그 자체는 v의 1차 함수다.

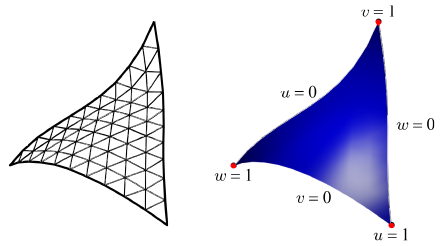
겹선형 패치의 정의역(Domain)은 두 매개변수 u와 v를 축으로 가지는 2차원 공간의 정사각형 영역으로 표현된다.

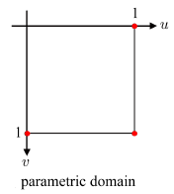
u와 v는 모두 [0, 1]의 범위를 가지는데, (u, v) 좌표는 겹선형 패치 위의 한 점 p(u, v)로 매핑된다. 아래는 uv 정의역 내에서 가중치들을 개념적으로 보여주는 그림이다.

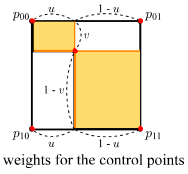
특정한 u와 v값은 uv 정의역을 네 개의 사각형으로 나누는데, 각 사각형의 면적은 ‘건너편’ 컨트롤 포인트의 가중치와 같다.

이렇게 만들어진 겹선형 패치를 렌더링하기 위해서는 그 패치를 삼각형 메시로 테셀레이션해야 한다. 즉, 겹선형 패치 위의 점들을 추출하고 이 점들을 삼각형으로 연결해야 한다. 아래는 균일한 샘플링을 통한 베지어 패치 테셀레이션의 과정을 보여주는 슈도 코드이다.

for each u in [0, 1]
    for each v in [0, 1]
        evaluate the patch using (u, v) to obtain (x, y, z)

처음에 u와 v를 균일하게 샘플하고, 샘플한 (u, v)를 앞서 구했던 p(u, v)에 대입하여 겹선형 패치 위의 3차원 점을 추출한다. 이렇게 생성된 점들로 삼각형 메시를 구성한다. 한편, p(u, v)는 행렬 형태로 표현할 수 있다.

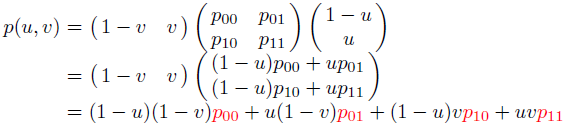
가운데 2 × 2 행렬은 컨트롤 포인트와 일치하며, 왼쪽의 행벡터와 오른쪽의 열벡터는 각각 v와 u의 1차 번스타인 다항식들을 원소로 가진다. u와 v의 순서를 바꾸어 계산을 진행해도 같은 모양의 겹선형 패치를 얻을 수 있으며, 테셀레이션이 끝난 겹선형 패치는 아래와 같은 폴리곤 메시가 된다.

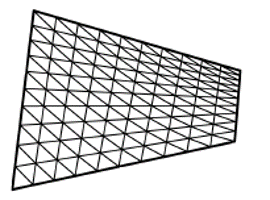
💡 겹선형 패치의 또 다른 예

---

🌱 2차 베지어 패치

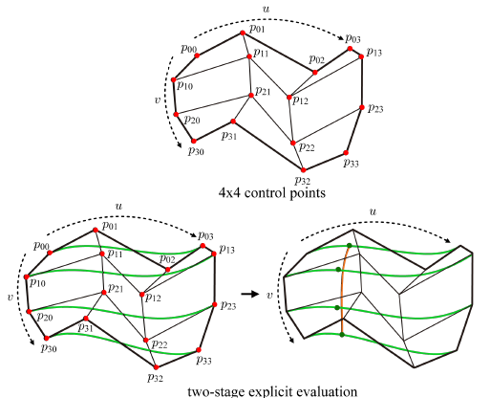
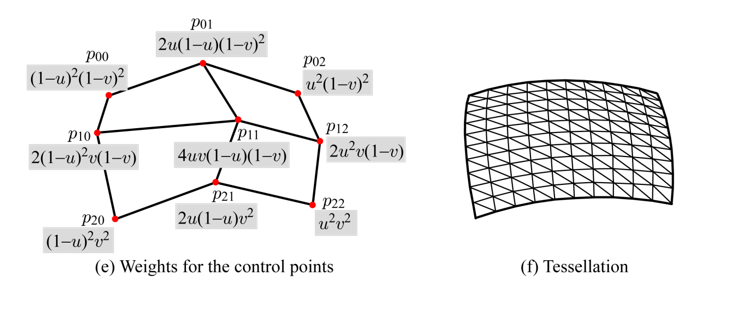
위 행렬 식에서 3 × 3 컨트롤 포인트를 사용하면 2차 베지어 패치(Biquadratic Bézier Patch)를 정의할 수 있다. 이를 위해 우선 u 방향으로 세 개씩 컨트롤 포인트를 모아 2차 베지어 곡선을 만들어야 한다.

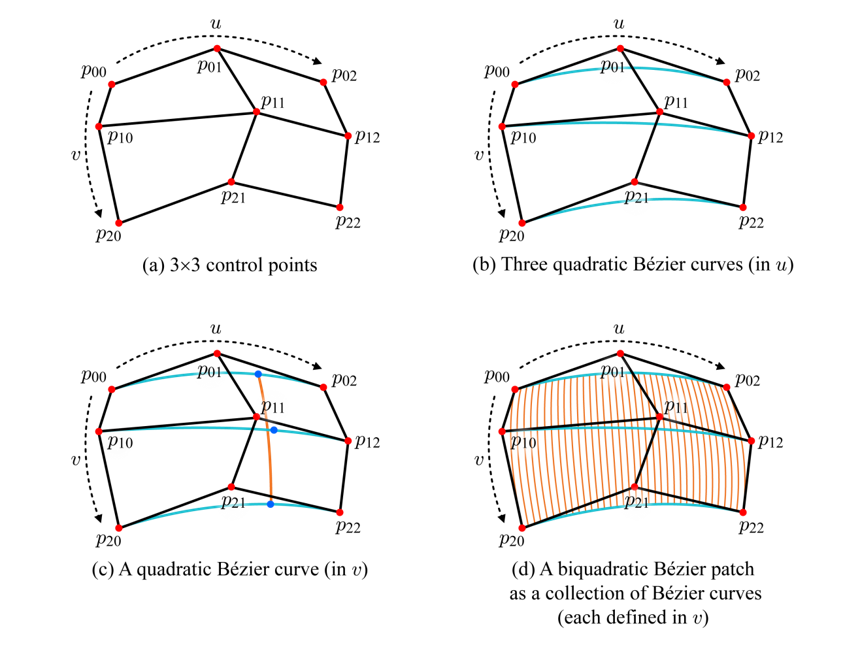
위 이미지의 그림-(b)는 이렇게 만들어진 세 개의 곡선을 보여준다. 이러한 2차 베지어 곡선 식에 특정한 u값을 대입하면, 각 곡선마다 하나의 점을 얻을 수 있다. 이 세 점을 컨트롤 포인트로 취하면 그림-(c)처럼 세로 방향으로 2차 베지어 곡선을 정의할 수 있다. 이 곡선은 v의 함수이다. 이후 과정은 1차 베지어 패치를 만드는 것과 동일하며 마찬가지로 아래와 같이 행렬 형태로 표현할 수 있다.

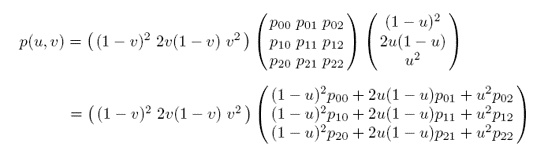
위 식에서 행렬 곱셈을 완료하면 2차 베지어 패치의 식을 얻을 수 있다.

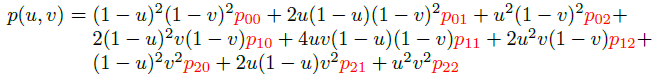
마찬가지로 2차 베지어 패치를 렌더링하기 위해서는 테셀레이션 과정이 필요하다.

위의 왼쪽 이미지는 각 점에 대한 가중치를 보여주고, 오른쪽 이미지는 테셀레이션 수행 후의 결과를 보여준다.

💡 2차 베지어 패치의 또 다른 예

한편, 드 카스텔조 알고리즘을 다른 방식으로 적용하여 동일한 2차 베지어 패치를 생성할 수도 있다.

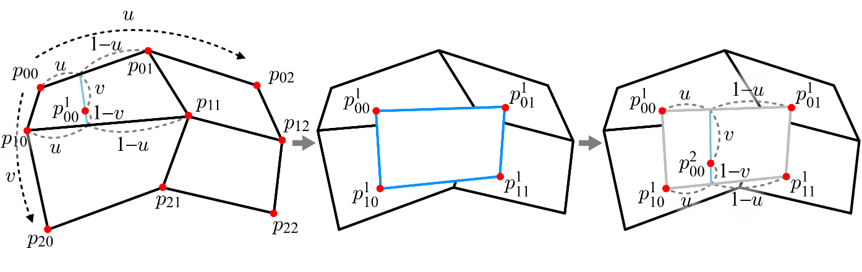
우선 3 × 3 컨트롤 포인트를 네 그룹으로 분리하면 2 × 2 컨트롤 포인트로 구성된 그룹이 되는데, 여기에 겹선형 보간을 수행한다. 첫 번째 겹선형 보간이 끝난 후 네 개의 점은 다음과 같이 정의된다.

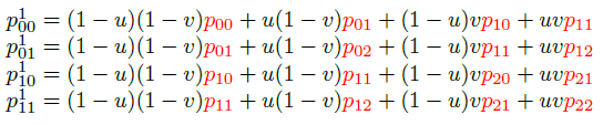
여기에 한 번 더 겹선형 보간을 수행한 결과는 다음과 같다.

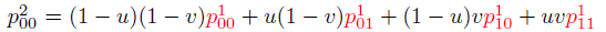
💡 위 식을 풀어보아요..🤗
p(u, v) = (1 - u)²(1 - v)²p₀₀ + 2u(1 - u)(1 - v)²p₀₁ + u²(1 - v)²p₀₂ + 2(1 - u)²v(1 - v)p₁₀ + 4uv(1 - u)(1 - v)p₁₁ + 2u²v(1 - v)p₁₂ + (1 - u)²v²p₂₀ + 2u(1 - u)v²p₂₁ + u²v²p₂₂

이 알고리즘을 반복적 겹선형 보간이라 부르며, 앞서 구했던 식과 위 식의 결과는 동일하다.

---

🌱 3차 베지어 패치

4 × 4 컨트롤 포인트를 사용하면 3차 베지어 패치(Bicubic Bézier Patch)를 정의할 수 있다. 행렬 형태로 표현하면 아래와 같다.

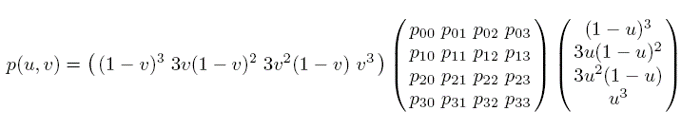
2차 베지어 패치와 동일한 방법으로 3차 베지어 패치를 정의할 수 있다.

물론 반복적 겹선형 보간을 사용해서도 만드는 것이 가능하다.

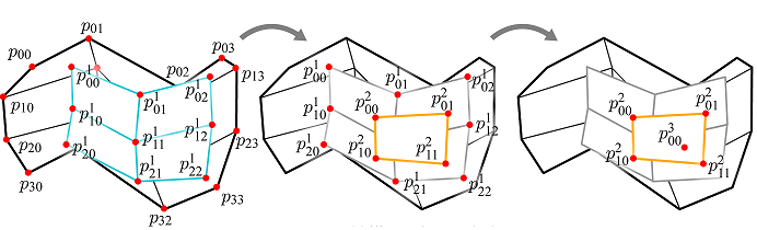
💡 3차 베지어 패치의 또 다른 예

베지어 패치는 컨트롤 포인트를 사용하여 편집된다.

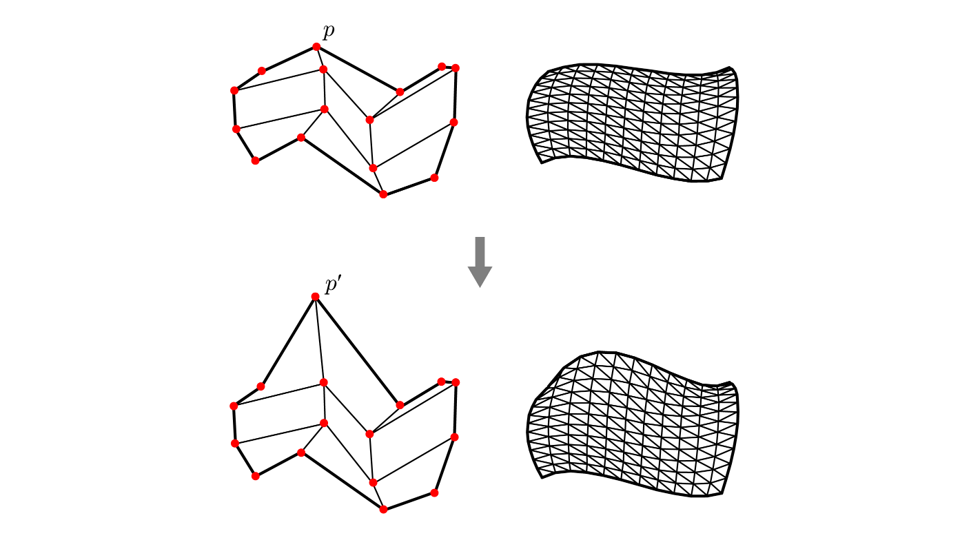
위 이미지에서, 컨트롤 포인트 하나가 움직일 때 곡면 모양이 상당히 변화되는 것을 알 수 있다. 이는 베지어 패치의 큰 장점이다. 베지어 패치를 테셀레이션하여 얻은 삼각형 메시의 정점들을 움직여 동일한 결과를 얻을 수도 있겠지만 이는 훨씬 고된 작업을 필요로 한다.

---

🌱 베지어 삼각형

이제까지 본 베지어 패치의 컨트롤 포인트들은 사각형 구조를 가졌었다. 삼각형 구조의 컨트롤 포인트에 의해 정의되는 패치인 베지어 삼각형(Bézier Triangle)에 대해 알아보자.

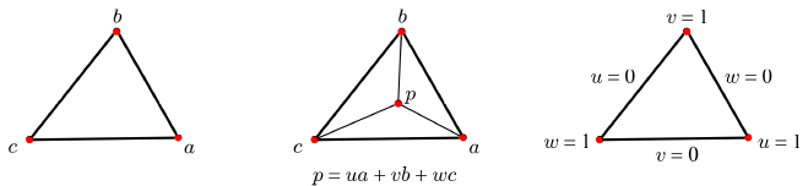
위 이미지는 세 개의 컨트롤 포인트 a, b, c로 정의되는 베지어 삼각형이다. 이를 1차 베지어 삼각형이라 부른다. 겹선형 패치를 정의하는 네 개의 컨트롤 포인트는 평면상에 존재하지 않을 수 있지만, 1차 베지어 삼각형의 세 개의 컨트롤 포인트는 언제나 하나의 평면을 이룬다. 따라서, 1차 베지어 삼각형은 보통의 삼각형과 동일하다고 볼 수 있다.

또한, 무게중심 좌표를 이용하면 각 컨트롤 포인트의 가중치도 정의된다. 마찬가지로, 각 컨트롤 포인트의 가중치는 ‘건너편’ 삼각형의 면적에 비례하며 무게중심 좌표가 (u, v, w)일 때, 삼각형 내부의 점 p는 다음과 같이 정의되며, 이를 무게중심 조합(Barycentric Combination)이라고 부른다.

p = ua + vb + wc

베지어 삼각형으로 곡면을 표현하기 위해서는 더 많은 컨트롤 포인트가 필요하다.

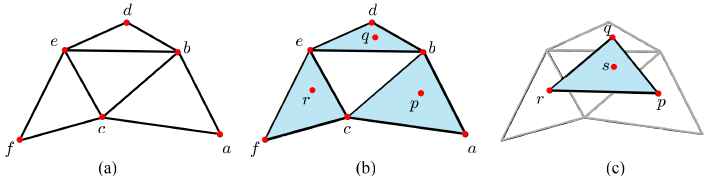
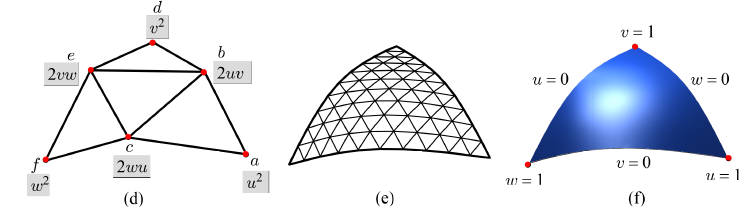
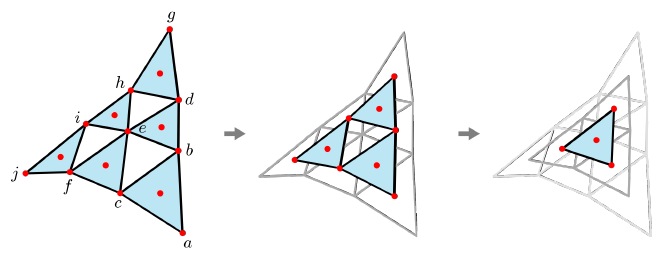
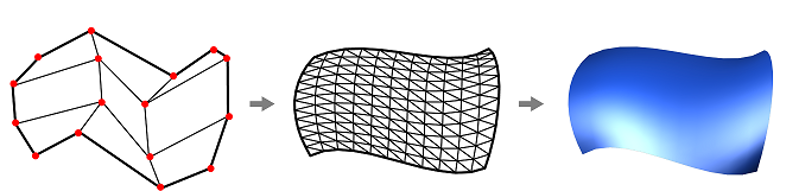
위 이미지의 그림-(a)는 삼각형 구조를 가진 6개의 컨트롤 포인트를 보여준다. 이러한 컨트롤 포인트로 반복적 무게중심 조합을 수행하면 곡면을 생성할 수 있다. 이는 2차 베지어 패치에서 사용한 반복적 겹선형 보간과 유사하며, 그림-(b)에서 색이 칠해진 세 개의 삼각형에 대하여 각각 무게중심 조합을 적용하여 구한 삼각형 <p, q, r>에 대해 한 번 더 무게중심 조합을 적용하면 그림-(c)의 s에 해당하는 최종 무게중심 좌표를 구할 수 있게 된다.

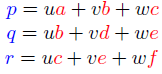
p, q, r이 위와 같을 때, 2차 베지어 삼각형의 식은 다음과 같다.

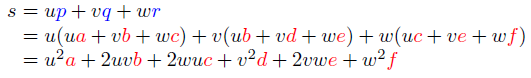
위 이미지에서 그림-(d)는 각 점의 가중치를 의미하며 마찬가지로 베지어 삼각형을 렌더링하기 위해서는 테셀레이션을 수행해야한다. 그 결과가 그림-(e)이다. 그림-(f)는 렌더링까지 모두 완료한 결과이다. 또한 각 곡선은 ‘건너편’ 가중치가 0일 때 정의된다는 경계 특성을 가지며, 그림-(f)에서 각 곡선에 대한 경계 가중치를 나타내고 있음을 알 수 있다.

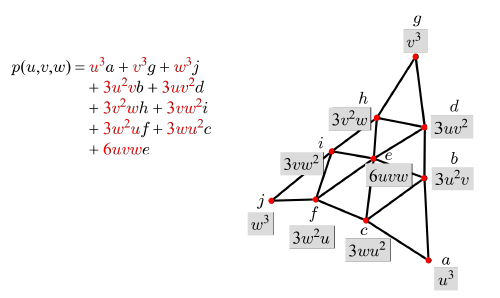
3차 베지어 삼각형도 마찬가지로 반복적 무게중심 조합을 거쳐 함수를 정의하게 된다. 렌더링 결과는 아래와 같다.

---

👻 글을 마치며

이번 시간에는 매개변수 곡선과 곡면에 대해 알아보았다. 곡선 하나 그리는 데에도 수많은 수학적 개념이 들어가 있다니..살려줘 계산이 귀찮은 것만 빼면 이해는 쉽게 할 수 있었던 것 같다. 확실히 그래픽스를 깊게 알면 알수록 보간이라는 개념이 얼마나 중요한지 새삼 깨닫는 것 같다. 그래도 그래픽스 공부 초반에 이해가 가지 않았던 부분을 스터디를 통해서 확실하게 이해했더니 그나마 머리가 굴러가는 것 같다..😭

---

출처
도서 관련 예제 GitHub
PPT 강의 자료 및 사진 출처

관련 도서
OpenGL ES를 이용한 3차원 컴퓨터 그래픽스 입문 - 한정현 지음