[Algorithm] 스택(Stack)과 큐(Queue)
👻 Stack
스택(Stack)은 후입선출(LIFO : Last-In-First-Out)의 알고리즘을 가지는 자료 구조이다. 탑이 쌓이는 구조라 생각하면 쉽다. 스택에 들어있는 데이터를 뺄 때 가장 마지막에 들어간 데이터부터 순서대로 빠지게 된다.
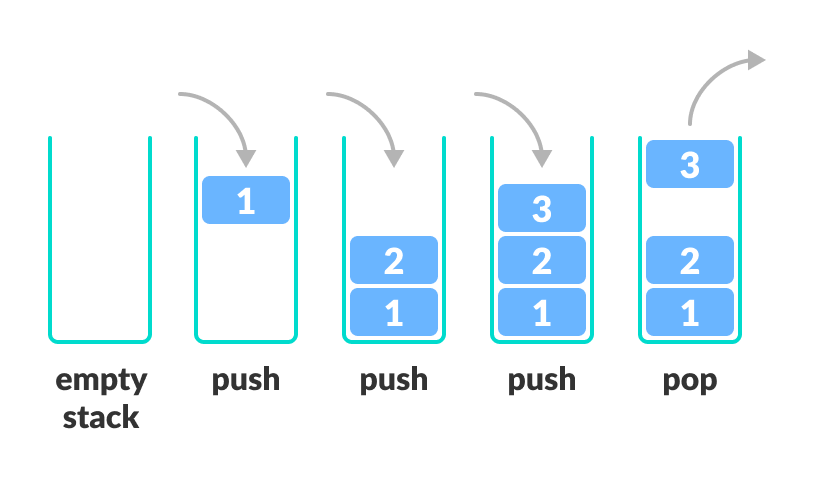
💡 되돌리기 같은 기능(Ctrl+Z)을 구현할 때 주로 활용된다.
🌱 구현 연습
#include <iostream>
#include <vector>
#include <list>
#include <stack>
using namespace std;
// Stack (LIFO Last-In-First-Out 후입선출)
// 활용
// - 되돌리기 같은 기능을 구현할 때 (Ctrl+Z)
// Stack 구현
// 동적 배열 사용 방식과 연결 리스트 사용 방식으로 나눌 수 있다.
template<typename T, typename Container = vector<T>>
class Stack
{
public:
void push(const T& value)
{
_container.push_back(value);
}
/*
// 성능 때문에 잘 사용하지 않는다. -> top 사용 선호
T pop()
{
T ret = _data[_size - 1];
_size--;
return ret; // T(const T&)
}
*/
void pop()
{
_container.pop_back();
}
T& top()
{
return _container.back();
}
bool empty() { return _container.empty(); }
int size() { return _container.size(); }
private:
// vector<T> _container;
// list<T> _container; // 동일한 동작을 한다. -> STL 컨테이너의 장점(인터페이스 통일화)
Container _container;
};
int main()
{
Stack<int> s; // vector
// Stack<int, list<int>> s; // list
// 삽입
s.push(1);
s.push(2);
s.push(3);
// 스택이 비었는지 확인
while (s.empty() == false)
{
// 최상위 원소
int data = s.top();
// 최상위 원소 삭제
s.pop();
cout << data << endl;
}
// 스택 사이즈
int size = s.size();
}
👻 Queue
큐(Queue)는 스택과 반대로 선입선출(FIFO : First-In-First-Out)의 알고리즘을 가지는 자료 구조이다. 터널을 통과하는 구조라 생각하면 쉽다. 큐에 들어있는 데이터는 가장 먼저 들어간 데이터 순서대로 빠지게 된다. 스택에 비해 활용 범위가 넓다.
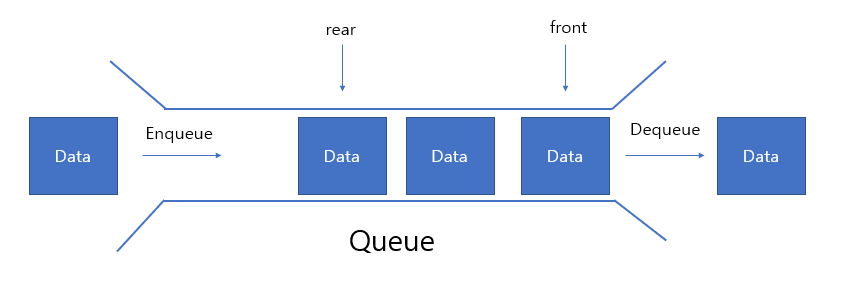
💡 대기열과 같은 기능을 구현할 때 주로 활용된다.
🌱 구현 연습
- 리스트 활용 방식
template<typename T> class ListQueue { public: void push(const T& value) { _container.push_back(value); } void pop() { // 효율이 좋지 않다. (동적 배열에서의 앞 요소 추가 및 삭제) // _container.erase(_container.begin()); // 리스트 사용 _container.pop_front(); } T& front() { return _container.front(); } bool empty() { return _container.empty(); } int size() { return _container.size(); } private: list<T> _container; // 덱(deque)을 사용해도 리스트와 비슷한 속도로 동작된다.(원래 코드는 덱으로 되어있음) }; - 배열 활용 방식
template<typename T> class ArrayQueue { public: ArrayQueue() { // _container.resize(100); } void push(const T& value) { if (_size == _container.size()) { // 증설 작업 int newSize = max(1, _size * 2); // 둘 중 큰 값을 리턴 vector<T> newData; newData.resize(newSize); // 데이터 복사 for (int i = 0; i < _size; i++) { int index = (_front + i) % _container.size(); newData[i] = _container[index]; } _container.swap(newData); _front = 0; _back = _size; } _container[_back] = value; _back = (_back + 1) % _container.size(); _size++; } void pop() { _front = (_front + 1) % _container.size(); _size--; } T& front() { return _container[_front]; } bool empty() { return _size == 0; } int size() { return _size; } private: vector<T> _container; int _front = 0; int _back = 0; int _size = 0; };
👻 오른손 법칙 개선
앞서 배운 스택을 이용해 오른손 법칙을 적용한 미로 길찾기 알고리즘을 개선해보자. 길을 찾을 때 막다른 길이면 돌아 나오던 부분을 스택을 이용하면 알 수 있다. 돌아가는 길이 스택의 가장 위에 존재하는 데이터와 같으면 돌아간다는 의미이기 때문이다. 이러한 성격을 활용하여 경로 배열을 다듬으면 다음과 같이 개선이 된다.
stack<Pos> s;
for (int i = 0; i < _path.size() - 1; i++)
{
if (s.empty() == false && s.top() == _path[i + 1])
s.pop();
else
s.push(_path[i]);
}
// 목적지 도착
if (_path.empty() == false)
s.push(_path.back());
vector<Pos> path;
while (s.empty() == false)
{
path.push_back(s.top());
s.pop();
}
std::reverse(path.begin(), path.end());
_path = path;
- 결과

👻 글을 마치며
이번 시간에는 스택과 큐에 대해 알아보고 스택을 이용해 이전 시간에 만들어보았던 미로 길찾기 알고리즘을 개선해보았다. 오른쪽으로만 꺾어서 가던 길에서 막힌 길을 되돌아오는 부분을 없앴다. 생각보다 단순해서 놀랐다. 동시에 내가 알고리즘을 조금은 더 어렵게 보고 있지 않았는지 생각하게 되었다. 앞으로는 부담 갖지 말고 할 수 있다는 마음가짐으로 천천히 문제를 풀어나가는 연습을 해야겠다.
Leave a comment