[Algorithm] 레드 블랙 트리(Red-Black Tree)
👻 레드 블랙 트리
레드 블랙 트리(Red-Black Tree)란 자가 균형 이진 탐색 트리이다. 이진 탐색 트리의 극단적인 경우 한쪽으로만 치우쳐진 트리가 완성될 가능성이 있다. 그렇게 되면 시간 복잡도는 O(log N)을 보장해주지 못한다. 이러한 문제점을 방지하기 위해 고안해낸 것이 바로 레드 블랙 트리이다.

🌱 특성
레드 블랙 트리는 5가지의 특성을 가진다.
- 노드는 레드 혹은 블랙 중의 하나이다.
- 루트 노드는 블랙이다.
- 모든 리프 노드(NIL)들은 블랙이다.
- 레드 노드의 자식노드 양쪽은 언제나 모두 블랙이다.
- 레드 노드가 두 개 이상 연달아 나타나는 것을 더블 레드(Double Red)라고 한다.
- 어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다.
👻 트리의 재구성
레드 블랙 트리에서 삽입, 삭제 등의 이벤트가 발생하여 트리의 균형이 맞지 않을 때, 즉 특성에 부합하지 않을 때 트리의 재구성이 필요하다. 회전(Rotation)과 색 변경(Color-Flipping)을 통해 트리의 균형을 맞춘다. 트리의 현재 상태에 따라 재구성 방법이 나뉜다.
🌱 Rotation
부모 노드가 레드, 삼촌 노드가 블랙일 경우에 왼쪽 혹은 오른쪽으로 노드를 회전시키는 방법이다.
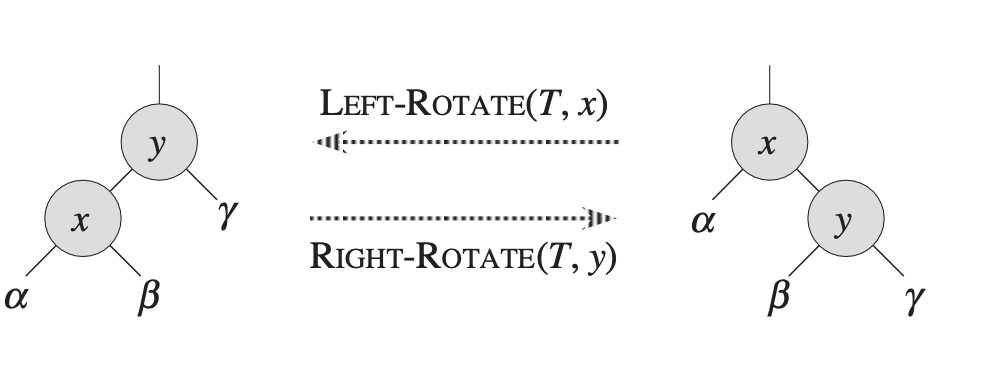
더블 레드가 발생했을 때, 노드의 모양을 보고 회전 방향이 결정된다. 조부모와 부모, 부모와 자식 노드 간의 연결된 방향이 다르면(꺾인 모양이면) 트라이앵글(Triangle) 타입이라고 하며 기준이 되는 노드는 부모 노드이다. 꺾인 방향에 따라 왼쪽, 혹은 오른쪽으로 회전시킨다.
한 번 회전을 하게 되면 트리의 균형이 맞춰질 때도 있지만 한 방향으로 뻗어진 구조가 될 수도 있다. 이러한 타입을 리스트(List) 타입이라 하고 반대로 한 번 더 회전을 시켜준다.
오른쪽 회전 시 x의 오른쪽 자식 노드가 y, 즉 x의 부모 노드의 왼쪽 자식 노드로 변환되고 왼쪽 회전은 반대로 되는 것을 알 수 있다.
- 노드 삽입
// Triangle 타입
if (node == node->parent->right)
{
node = node->parent;
LeftRotate(node);
}
// List 타입
node->parent->color = Color::Black;
node->parent->parent->color = Color::Red;
RightRotate(node->parent->parent);
- 회전 함수
void BinarySearchTree::LeftRotate(Node* x)
{
Node* y = x->right;
x->right = y->left; // [2];
if (y->left != _nil)
y->left->parent = x;
y->parent = x->parent;
if (x->parent == _nil)
_root = y;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
}
void BinarySearchTree::RightRotate(Node* y)
{
Node* x = y->left;
y->left = x->right; // [2];
if (x->right != _nil)
x->right->parent = y;
if (y->parent == _nil)
_root = x;
else if (y == y->parent->right)
y->parent->right = x;
else
y->parent->left = x;
x->right = y;
y->parent = x;
}
🌱 Color-Flipping
노드의 색을 변경하는 방법이며 해당 방법을 사용하기 위해선 두 가지 경우가 존재한다.
- 부모 노드와 삼촌 노드 모두 레드로 동일하다면 부모 노드와 삼촌 노드 모두 블랙으로 바꿔주고 조부모 노드를 레드로 바꿔주면 트리 변경은 종료된다.
// 색상 변경 node->parent->color = Color::Black; uncle->color = Color::Black; node->parent->parent->color = Color::Red; - 부모 노드가 레드, 삼촌 노드가 블랙일 때, 한 방향으로 이어진 리스트 타입이라면 부모 노드와 조부모 노드의 색을 각각 블랙, 레드로 변경해주고 회전을 진행한다.
node->parent->color = Color::Black; node->parent->parent->color = Color::Red; LeftRotate(node->parent->parent);
👻 Delete
레드 블랙 트리에서 노드의 삽입은 일반 이진 탐색 트리와 크게 다르지 않다. 단, 노드를 삽입했을 때 레드 블랙 트리의 특성에 부합할 수 있도록 회전과 색 변경을 통해 트리의 재구성이 일어난다. 노드를 삭제할 때도 마찬가지로 트리의 재구성이 일어나지만 삽입과는 다르게 과정이 아주 복잡하다. 일단 삭제한 노드의 위치에 블랙을 하나 추가하여 더블 블랙(Double Black, 이하 DB) 상태로 만든 후 트리의 재구성 과정을 진행한다. 트리의 재구성 방법은 크게 6가지의 케이스로 나눌 수 있다.
- 삭제할 노드가 레드일 때
- 그냥 삭제하면 끝이다. (리프 노드가 아니라면 다른 케이스에 의해 재구성 될 것임)
- 루트 노드가 DB일 때
- 그냥 추가 Black을 삭제하면 끝이다.
- DB의 형제(Sibling) 노드가 레드일 때
s = black,p = red(s ↔ p 색상 교환)- DB 방향으로
Rotate(p)- 다른 케이스로 이동
- DB의 형제 노드가 블랙이고, 형제 노드의 양쪽 자식도 모두 블랙일 때
- 추가 Black을 부모 노드로 이전
- p가 레드면 블랙이 됨
- p가 블랙이면 DB가 됨
s = red- p를 대상으로 알고리즘을 이어서 실행한다. (DB가 여전히 존재할 경우)
- DB의 형제 노드가 블랙이고 형제 노드의 자식 중 DB와 가까운 자식(Near Child) 노드가 레드이고, 먼 자식(Far Child) 노드가 블랙일 때
- s ↔ near 색상 교환
- far 방향으로
Rotate(s)- 6번 케이스로 이동
- DB의 형제 노드가 블랙이고, 먼 자식(Far Child) 노드가 레드일 때
- p ↔ s 색상 교환
far = black- DB 방향으로
Rotate(p)- 추가 Black 제거
- 코드
void BinarySearchTree::DeleteFixup(Node* node)
{
// 삭제할 노드
Node* x = node;
// [Case1], [Case2]
while (x != _root && x->color == Color::Black)
{
// [p]
// [x(B)] [s(?)]
if (x == x->parent->left)
{
// [Case3]
Node* s = x->parent->right;
if (s->color == Color::Red)
{
s->color = Color::Black;
x->parent->color = Color::Red;
LeftRotate(x->parent);
s = x->parent->right;
}
// [Case4]
if (s->left->color == Color::Black && s->right->color == Color::Black)
{
s->color = Color::Red;
x = x->parent;
}
else
{
// [Case5]
if (s->right->color == Color::Black)
{
s->left->color = Color::Black;
s->color = Color::Red;
RightRotate(s);
s = x->parent->right;
}
// [Case6]
s->color = x->parent->color;
x->parent->color = Color::Black;
s->right->color = Color::Black;
LeftRotate(x->parent);
x = _root;
}
}
else
{
// [Case3]
Node* s = x->parent->left;
if (s->color == Color::Red)
{
s->color = Color::Black;
x->parent->color = Color::Red;
RightRotate(x->parent);
s = x->parent->left;
}
// [Case4]
if (s->right->color == Color::Black && s->left->color == Color::Black)
{
s->color = Color::Red;
x = x->parent;
}
else
{
// [Case5]
if (s->left->color == Color::Black)
{
s->right->color = Color::Black;
s->color = Color::Red;
LeftRotate(s);
s = x->parent->left;
}
// [Case6]
s->color = x->parent->color;
x->parent->color = Color::Black;
s->left->color = Color::Black;
RightRotate(x->parent);
x = _root;
}
}
}
x->color = Color::Black;
}
👻 글을 마치며
이번 시간에는 레드 블랙 트리에 대해 알아보았다. 처음 들어보는 트리였는데 각 노드에 레드, 블랙을 추가하여 이진 탐색 노드의 균형을 맞춰주는 것으로 이해할 수 있었다. 거의 공식(?)과 비슷하다고 느껴져서 특성을 외워야만 했는데 처음엔 당연히 이해하기 힘든 부분이 조금 있었지만 그래도 지금은 많이 익숙해진 것 같다. 그리고 노드의 삽입은 크게 어렵지 않았는데(그래도 이해하는데 한시간 조금 넘게 걸린 것 같다.) 삭제가 진짜 헬인 것 같다.. 완벽히 이해가 될 때까진 그림을 통해서 복습하고 또 복습해야 할 것 같다. 그림이 이해가 된다면 자연스레 코드도 이해가 될테니 말이다.
Leave a comment