[Algorithm] 이진 탐색 트리(Binary Search Tree)

👻 이진 탐색

이진 탐색(Binary Search)는 전체 데이터를 순회하는 방법이 아닌 조건을 정해 특정한 값의 위치를 찾는 알고리즘이다. 정렬된 데이터라는 제한적인 상황이 존재하고, 중간값을 임의의 값으로 선택하여 대소 비교를 통해 탐색 범위를 좁혀나가는 방식이다.

정렬된 배열이 아래와 같이 존재한다.
[1][8][15][23][32][44][56][63][81][91]

Q. 82라는 숫자가 배열에 있는가?
A.

• 순차적 탐색
  • 데이터를 처음부터 하나씩 비교하며 탐색한다.
  • 시간 복잡도는 O(N)
• 이진 탐색
  • 중간값을 설정하여 비교하는 과정을 반복하며 탐색한다.
  • 시간 복잡도는 O(log N) (훨씬 효율적이다)

정렬된 데이터기 때문에 이진 탐색이 가능하지만 중간 삽입/삭제가 느리다는 단점과 정렬된 연결 리스트로는 이진 탐색 알고리즘을 적용할 수 없다. 연결 리스트는 임의 접근이 불가하기 때문이다.

• 이진 탐색 구현

{
    int left = 0;
    int right = (int)numbers.size() - 1;

    while (left <= right)
    {
        int mid = (left + right) / 2;
        if (n < numbers[mid])
            right = mid - 1;
        else if (n > numbers[mid])
            left = mid + 1;
        else
        {
            cout << "Found!" << endl;
            break;
        }
    }
}

이러한 단점을 보완하기 위해 이진 탐색 트리(Binary Search Tree) 구조가 나오게 되었다.

---

👻 이진 탐색 트리

이진 탐색 트리(Binary Search Tree)는 이진 탐색 알고리즘을 기반으로 트리와 합쳐진 자료 구조를 의미한다. 최대 2개의 자식 노드를 가질 수 있으며 부모 노드를 기준으로 왼쪽 노드는 작은 수, 오른쪽 노드는 큰 수로 정렬되어 트리가 설정된다.

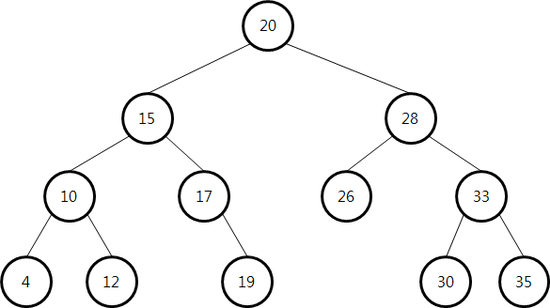
💡 완전 이진 트리 구조와는 다르니 혼동하지 않도록 주의하자.

---

🌱 구현 연습

• 노드

struct Node
{
	Node*	parent = nullptr;
	Node*	left = nullptr;
	Node*	right = nullptr;
	int		key = {};	// key == data
};

기본적으로 부모 노드를 가리키는 포인터와 왼쪽, 오른쪽 자식 노드를 가리키는 포인터, 그리고 해당 노드의 키값을 가지는 노드로 구성되어있다.

• Min, Max 찾기

Node* BinarySearchTree::Min(Node* node)
{
	while (node->left)
		node = node->left;
	return node;
}

Node* BinarySearchTree::Max(Node* node)
{
	while (node->right)
		node = node->right;
	return node;
}

이진 탐색 트리에서 가장 왼쪽 끝에 위치한 노드가 가장 작은 수, 가장 오른쪽 끝에 위치한 노드가 가장 큰 수를 나타낸다.

• Search

Node* BinarySearchTree::Search(Node* node, int key)
{
	if (node == nullptr || key == node->key)
		return node;

	if (key < node->key)
		return Search(node->left, key);
	else
		return Search(node->right, key);
}

Node* BinarySearchTree::Search2(Node* node, int key)
{
	while (node && key != node->key)
	{
		if (key < node->key)
			node = node->left;
		else
			node = node->right;
	}

	return node;
}

트리의 재귀적 속성을 이용하면 재귀함수를 통해 노드를 탐색하는 기능을 쉽게 구현할 수 있지만 경우에 따라 하나의 반복문을 통해 찾는 것도 방법이다. 아무래도 트리의 크기가 커지면 하나의 while문을 통해 탐색하는 것이 재귀함수를 이용하는 것보다 빠를 것이다.

• 다음으로 큰 노드 찾기

Node* BinarySearchTree::Next(Node* node)
{
	if (node->right)
		return Min(node->right);

	Node* parent = node->parent;

	while (parent && node == parent->right)
	{
		node = parent;
		parent = parent->parent;
	}

	return parent;
}

일단 우측 노드가 존재한다는 것은 현재 노드보다 큰 수들만 모여있기 때문에, 우측 노드의 서브트리에서 가장 작은 수를 찾으면 다음으로 큰 수일 것이다.

우측 노드가 없다면 부모 노드로 올라가게 되고, 우측 노드를 가지고 있지 않은 노드가 그 중에서 가장 작은 수를 가지는 노드가 될 것이다.

• Insert

void BinarySearchTree::Insert(int key)
{
	Node* newNode = new Node();
	newNode->key = key;

	if (_root == nullptr)
	{
		_root = newNode;
		return;
	}

	Node* node = _root;
	Node* parent = nullptr;

	while (node)
	{
		parent = node;
		if (key < node->key)
			node = node->left;
		else
			node = node->right;
	}

	newNode->parent = parent;

	if (key < parent->key)
		parent->left = newNode;
	else
		parent->right = newNode;
}

루트 노드부터 대소 비교를 시작하여 삽입할 위치를 찾는다. 키값이 비교하는 노드의 키값보다 작으면 왼쪽, 크면 오른쪽 서브트리를 계속 탐색하게 될 것이다.

그러다 다음 노드가 없는 리프 노드에 도달하게 되는데, 그 때 새로 만든 노드를 추가하면 삽입 기능은 완성이다.

💡 추가한다는 것은 노드 간의 연결을 의미한다.

• Delete

void BinarySearchTree::Delete(int key)
{
	Node* deleteNode = Search(_root, key);
	Delete(deleteNode);
}

void BinarySearchTree::Delete(Node* node)
{
	if (node == nullptr)
		return;

	if (node->left == nullptr)
		Replace(node, node->right);
	else if (node->right == nullptr)
		Replace(node, node->left);
	else
	{
		// 자식 노드가 2개 모두 있을 때
		// 다음 데이터 찾기
		Node* next = Next(node);
		node->key = next->key;
		Delete(next);
	}
}

// u 서브트리를 v 서브트리로 교체
void BinarySearchTree::Replace(Node* u, Node* v)
{
	if (u->parent == nullptr)
		_root = v;
	else if (u == u->parent->left)
		u->parent->left = v;
	else
		u->parent->right = v;

	if (v)
		v->parent = u->parent;

	delete u;
}

노드 삭제는 자식이 0~1개일 때와 2개일 때로 나뉜다.

0~1개일 때는 자식 노드와 해당 노드의 위치를 바꿔주고 연결 정보만 수정해주면 쉽게 완료된다. 만약, 자식 노드가 없어 바꾸려는 노드가 null일 때에는 부모 노드의 연결 정보를 null로 바꿔주기 때문에 예외처리 없이 사용 가능하다.

자식 노드가 2개 모두 존재한다면, 삭제하려는 노드보다 다음으로 큰 수의 노드를 찾아 위치를 바꿔주고 해당 노드를 삭제시키는 작업을 반복하면 트리가 알아서 정리될 것이다.

---

🌱 트리 순회

이진 탐색 트리를 순회하는 방법은 전위 순회, 중위 순회, 후위 순회가 있다. 왼쪽 노드, 중간 노드, 오른쪽 노드의 탐색 순서에 따라 나뉜다. 중간 노드의 위치에 따라 이름이 나뉜다고 생각하면 구분이 쉽다.

• 전위 순회 (Preorder Traversal)
  중간 노드 👉 왼쪽 노드 👉 오른쪽 노드 순으로 방문한다.

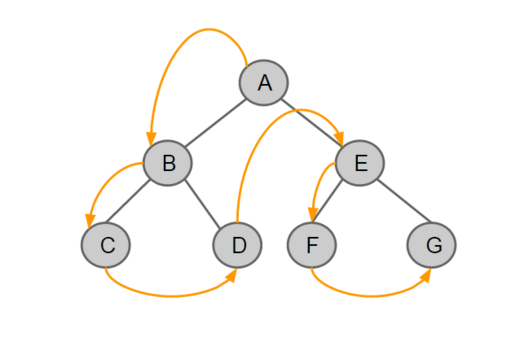
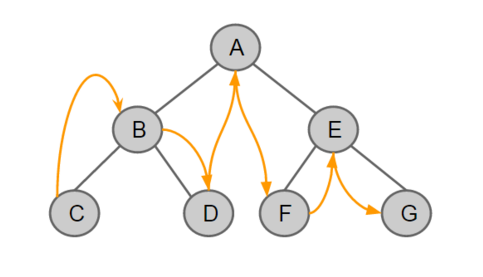
• 중위 순회 (Inorder Traversal)
  왼쪽 노드 👉 중간 노드 👉 오른쪽 노드 순으로 방문한다.

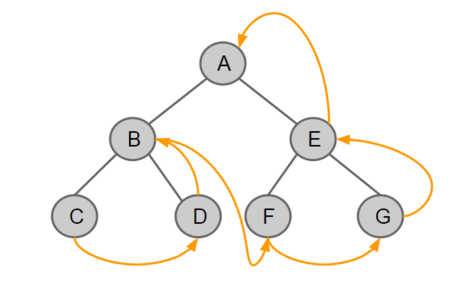
• 후위 순회 (Postorder Traversal)
  왼쪽 노드 👉 오른쪽 노드 👉 중간 노드 순으로 방문한다.

---

👻 글을 마치며

이번 시간에는 이진 탐색 트리에 대해 알아보았다. 개인적으로 이진 트리 구조를 깔끔해서 좋아하는데 코드로 나타내려니 복잡하긴 한 것 같다. 😂 그래도 공부하는 내내 흥미로웠고 혼자 코드를 복기해보니 생각보다 간단해서 다행이었다.

---

출처
인프런 Rookiss님 강의
자료구조 :: 이진 트리 순회 - 전위 순회, 중위순회, 후위순회