[Algorithm] 빅오 표기법(Big-O Notation)

👻 Big-O Notation

알고리즘의 효율을 측정하기 위해 빅오 표기법(Big-O Notation)을 사용한다. 시간 복잡도를 나타내는 데 쓰이며 다음과 같이 표기한다.

O(f(n))

---

🌱 1단계

수행되는 연산(산술, 비교, 대입 등)의 개수를 대략적으로 판단한다.

• O(1)

  int Add(int n)
  {
    return n + n;
  }
  

• O(N + 1)

  int Add2(int n)
  {
    int sum = 0;
    for (int i = 0; i < n; i++)
        sum += i;
    return sum;
  }
  

• O(N² + 1)

  int Add3(int n)
  {
    int sum = 0;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            sum += 1;
    return sum;
  }
  

---

🌱 2단계

영향력이 가장 큰 대표 항목만 남기고 삭제시킨다. 또한 상수는 무시한다.

int Add4(int n)
{
    int sum = 0;

    for (int i = 0; i < n; i++)
        sum += i;

    for (int i = 0; i < 2 * n; i++)
        for (int j = 0; j < 2 * n; j++)
            sum += 1;

    sum += 1234567;

    return sum;
}

위의 함수를 2단계 규칙에 맞게 계산하면 시간 복잡도를 다음과 같이 구할 수 있다.

O(1 + N + 4 * N² + 1)
= O(4 * N²)
= O(N²)

💡 O는 Order Of라고 읽는다.

---

👻 Big-O 표기법의 의의

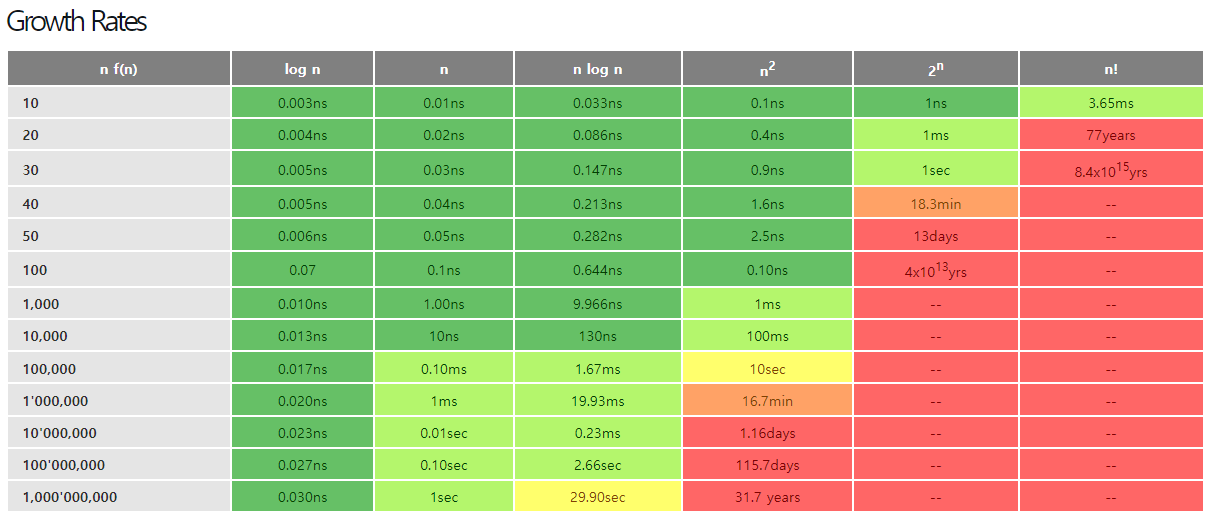
입력 N의 크기에 따라 성능이 영향을 받는 정도를 나타낸다.

초록색은 안정적인 부분이고 빨간색은 위험하니 조심해서 코드를 짜야한다.

💡 모든 시간 복잡도 중에서 O(log N)이 가장 효율이 좋다.

---

👻 글을 마치며

이번 시간에는 알고리즘 OT 겸 빅오 표기법에 대해 간단하게 알아보았다. 코테를 준비했을 때 잠깐 공부했던 기억이 있다. 이제 알고리즘 공부를 진행하면서 수시로 시간 복잡도를 계산하는 버릇을 들여야겠다.

---

출처
인프런 Rookiss님 강의
About Big-O Notation